ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 37
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Геометрическая интерпретация целевой функции.Пусть ОДР задачи ЛП – непустое множество.Выберем произвольное значение целевой функции 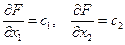, получим . Это уравнение прямой линии. В точках прямой целевая функция сохраняет одно и то же постоянное значение . Считая в равенстве параметром, получим уравнение семейства параллельных прямых, называемых линиями уровня целевой функции. Найдем частные производные целевой функции по x1 и x2: .Частная производная функции показывает скорость её возрастания вдоль данной оси. с1 и с2 – скорости возрастания соответственно вдоль осей Ox1 и Ox2. Вектор называется градиентом функции. Он показывает направление наискорейшего возрастания целевой функции. Вектор указывает направление наискорейшего убывания целевой функции Его называют антиградиентом.Вектор перпендикулярен к прямой семейства .Из геометрической интерпретации элементов ЗЛП вытекает следующий порядок её графического решения.1. С учетом системы ограничений строится область допустимых решений.2. Строится вектор
.
3. Проводится произвольная линия, перпендикулярная к вектору 
.
4. При решении задачи на максимум перемещается линия уровня в направлении вектора так, чтобы она касалась области допустимых решений в ее крайнем положении.
В случае задачи на минимум линия уровня перемещается в антиградиентном направлении.
5. Определяется оптимальный план 
и экстремальное значение целевой функции 
.