ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 23
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лекция 4
Диэлектрическая проницаемость. Электроѐмкость и энергия конденсаторов
Вектор поляризации диэлектрика. Диэлектрическая проницаемость среды
Для количественной характеристики поляризации диэлектрика служит специальная вели- чина, называемая вектором поляризации. Вектором поляризации диэлектрика называют отно- шение векторной суммы электрических дипольных моментов всех молекул, заключенных в неко- тором объеме Δ???? диэлектрика, к величине этого объема:
????⃗→ = 1Δ????
∑ ????⃗⃗⃗→????.
j
Опыт показывает, что для не слишком сильных электрических полей вектор поляризации линейно зависит от напряженности ????⃗→ электрического поля в диэлектрике. В простейшем случае изотропных диэлектриков (то есть диэлектриков, величина поляризуемости которых не зависит от направления вектора ????⃗→) эту связь можно записать в виде:
????⃗→ = æsO????⃗→,
где æ называют диэлектрической восприимчивостью вещества. Если æ не зависит от координат, то такой диэлектрик называют однородным.
Важную роль в электростатике и электродинамике играет величина s = 1 æ, называемая (относительной) диэлектрической проницаемостью вещества. Дело в том, что оказывается справедливо следующее утверждение:
Напряженность электрического поля, создаваемого любой системой точечных зарядовили проводников с фиксированной величиной зарядов в однородном изотропном диэлектрике сдиэлектрической проницаемостью s, занимающем все пространство, где есть поле, вразменьше, чем поле этой же системы зарядов и проводников в вакууме. Очевидно, что при оди- наковом выборе нулевой точки потенциал любой точки поля в описанной выше ситуации при наличии диэлектрика также в s раз меньше, чем при его отсутствии.
Замечание. Можно также доказать, что если в сформулированном выше утверждении од- нородный изотропный диэлектрик занимает только часть области, где есть поле, но эта часть ограничена эквипотенциальной поверхностью, то по сравнению со случаем отсутствия ди- электрика поле вне диэлектрика не изменится, а поле внутри диэлектрика уменьшится в s раз.
Электроемкость уединенного проводника
Рассмотрим уединенный проводник, то есть проводник расположенный достаточно далеко от всех других заряженных и незаряженных тел. Поместим на него заряд q. Он распределится по
поверхности проводника каким-то образом (так, что поле в проводнике равно нулю) и создаст во всем пространстве некоторое поле ????⃗→ , и, значит, точки проводника будут иметь некоторый одинаковый потенциал ф. Поместим теперь на проводник еще такой же заряд q. По теореме единственности он распределится так же, как и предыдущий заряд. В результате поле во всем пространстве удвоится, следовательно, удвоится и потенциал проводника. Из сказанного следует, что отношение заряда уединенного проводника к его потенциалу не зависит от заряда про- водника. Это позволяет ввести понятие электроемкости (или просто емкости) C уединенного проводника, которая равна отношению заряда проводника к его потенциалу:
=
Из сказанного выше следует, что емкость уединенного проводника определяется исклю- чительно его формой и геометрическими размерами.
Из определения следует, что единица измерения емкости
1
= 1 1 B
Иными словами, емкостью в один фарад обладает такой уединенный проводник, потенциал которого при сообщении ему заряда 1 Кл равен 1 В.
Нетрудно понять, что емкость уединенного сферического проводника
???? = 4????sO????
где R – радиус сферы (т.к. =).
4????????0 ????
Приведенные рассуждения сохраняют свою силу и в том случае, если проводник окружен другими незаряженными телами. Однако наличие вблизи проводника других тел
, и, в частности диэлектриков, изменяет его емкость, так как потенциал проводника зависит и от электрических полей, создаваемых зарядами, наведенными в окружающих телах в следствие электростатиче- ской индукции или поляризации. В частности, емкость проводящей сферы радиуса R, помещен- ной в однородный диэлектрик с диэлектрической проницаемостью s увеличивается в s раз:
???? = 4????ssO????
(так как поле вокруг сферы, и, следовательно, ее потенциал, уменьшаются в s раз).
Взаимная электроемкость двух проводников. Конденсаторы
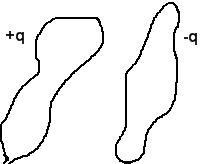Рассмотрим теперь систему из двух проводников вотсутствиивнешнего электрического поля. Сообщим им равные по модулю заряды противоположного знака. В результате между проводниками возникнет разность потенциалов. Рассуждая так же, как в случае одного проводника, нетрудно понять, что отношение заряда qк разности потенциалов междупроводниками 1 2 не зависит от величины q. Это отношение, точнее его модуль, называют
взаимной емкостью двух проводников:
???? = |
????
|1 2
Так как силовые линии начинаются на положительных зарядах и заканчиваются на отрицатель- ных, а потенциал, как следует из его определения, уменьшается при движении по направлению силовых линий, то | 1 2| = + −, где + потенциал проводника, заряженного положи- тельно, а − – отрицательно. Поэтому:
???? =
|????|
+ −
????
= .−
Взаимная емкость двух проводников зависит от их формы, размеров и взаимного распо- ложения, а также от среды, в которой они находятся.
Определение. Конденсатором называется система двух разноименных заряженных рав- ными по абсолютной величине зарядами проводников, имеющих такую форму и расположение друг относительно друга, что поле, создаваемое такой системой, сосредоточено в ограниченной области пространства. Сами проводники при этом называются обкладками конденсатора.
Электроемкостью конденсатора называется взаимная емкость его обкладок. Примером конденсатора является любой полый провод-ник, в полости которого находится другой проводник. При этом полость между проводниками может быть заполнена каким- нибудь диэлектриком.
Емкость плоского и сферического конденсаторов
Наиболее часто используются плоские и сферические конденсаторы.
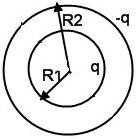Сферический конденсатор состоит из двух проводящих концентрических сфер, про- странство между которыми может быть заполнено диэлектриком с диэлектрической проницаемо- стью s. Такая система создает не равное нулю поле только между обкладками,причем это поле равно полю точечного заряда, уменьшенному в s раз:
Соответственно = 1
1
???? =4????sO
???? , и ???? s ????2.
= ( 1 1 ) = ????2−????1 .
4????????0???? ???? O
+ − 4????????0????
????1
????2
4????????0????????2????1
Поэтому емкость сферического конденсатора
2
−
|????|
????2????1
???? =+
= 4????sOs ????
.
????1
Видно, что при наличии диэлектрика емкость возрастает (для всех диэлектриков s 1 . Однако, наличие диэлектрика может уменьшать напряжение пробоя конденсатора – разность по- тенциалов между обкладками, при которой происходит электрический пробой слоя диэлектрика.
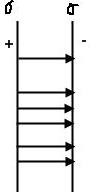
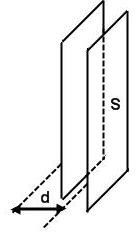Часто используется также плоский конденсатор, состоящий из двух проводящих парал- лельных пластин одинаковой формы (площади S), расположенных напротив другдруга на расстоянии d, малом по сравнению с поперечными размерами пластин. Поэтому электрическое поле между пластинами приближенно равно
???? =
????
2sO
???? ????
+ = ,2sO sO
где ???? = | |????
– модуль поверхностной плотности заряда на каждой из пластин.
Следовательно
+ −
= ???????? = | | ,
????0????
и, значит, емкость плоского конденсатора
???? =
sO????
.????
Если плоский конденсатор, обкладки которого имеют заряды фиксированной
величины, полностью заполнить диэлектриком с диэлектрической проницаемостью s, то поле и разность потенциалов между обкладками уменьшатся в s раз, и, значит, емкость плоского кон- денсатора увеличится в s раз.