ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 24
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Подчеркнѐм, что модель плоского конденсатора, в которой считается, что электрическое поле однородно в области между пла- стинами и равно нулю вне этой области, имеет ограниченную при- менимость. Дело в том, что электростатическое поле в такой модели
???? ????
является не потенциальным: работа по замкнутому контуру ABCD (см. рисунок) не равна нулю, что невозможно. На самом деле электростатическое поле вблизи краев плоского конденсатора неоднородно и вне границ конденсатора поле не равно нулю, хоть и очень слабое. Нетрудно по-
нять, что модель плоского конденсатора работает тем лучше, чем меньше отношение 2. Однако????
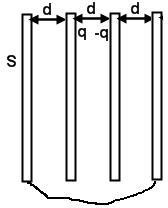в ряде случаев краевыми эффектами нельзя полностью пренебречь ни при каких условиях.Пример. Четыре первоначально незаряженные одинаковые пластины поместили на расстоянии d друг от друга. Две средних пластины зарядили заря- дами +q и –q. А две крайние соединили проводником. Чему будут равны заряды на крайних пластинах (????2 ???? .
Решение. Если пользоваться моделью плоского конденсатора, то, каза-
лось бы, крайние пластины просто “не узнают” о том, что средние пластины зарядили (поле сна-
ружи от средних пластин в этой модели равно нулю). Однако на са- мом деле все не так из-за описанных выше краевых эффектов. В ре- зультате правая пластина окажется заряженной положительно, а ле- вая – отрицательно. Величину заряда найдем из условия, что крайние пластины имеют одинаковый потенциал:
−???? ???? ????
????1???? − ????2???? + ????1???? = 0
???? = 2????
0
{ Q ????−Q ⇒ { 2 1 ⇒ ???? = ????/3 ????1 = ????????
, ????2 =
????????0
???? − ???? = 2????
Расчет емкости конденсатора в случае обкладок произвольной формы является достаточно сложной задачей. Однако, и в этом
????
случае заполнение всего пространства между обкладками диэлек- триком с диэлектрической проницаемостью s приводит к увели- чению емкости конденсатора в s раз (за счет уменьшения в s раз поля и, следовательно, разности потенциалов между обкладками).Параллельное и последовательное соединение конденсаторов.
Система, полученная в результате соединения пластин нескольких конденсаторов провод- никами (пренебрежимо малой емкости), называется батареей конденсаторов. В ряде случаев батарею конденсаторов можно описать как один конденсатор емкостью С.
Если в системе двух конденсаторов с емкостями ????1 и ????2 пластины разных конденсаторов соединены попарно (батарея содержит два изолированных проводника), то такое соединение называется параллельным. Два (и более) параллельно соединенных конденсатора всегда можно описать как один конденсатор некоторой емкостью C. В этом случае общим для всех конденса-
торов является разность потенциалов между обкладками Δф, и мы имеем:
????1 = ????1Δф, ????2 = ????2Δф.
Поэтому суммарный заряд, находящийся на батарее, равен
???? = ????1 + ????2 = (????1 + ????2)Δф.
И, следовательно, емкость батареи
????1
????
????
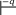???? = Δф = ????1 + ????2.Итак, емкость батареи конденсаторов, соединенных параллельно, равна
????
сумме емкостей отдельных конденсаторов. Если у двух конденсаторов с емкостями ????1 и ????2 соединена одна пара пластин (батарея содержит три изолированных провод- ника), то такое соединение конденсаторов называется последова-
тельным. Последовательносоединенныеконденсаторыможнорассматриватькакновыйкон-денсатортолько,еслисоединенныемеждусобойобкладкивцеломэлектронейтральны!
В этом случае одинаковым для всех конденсаторов является заряд q, равный заряду бата- реи, и мы можем написатьНо 1
???? Δф1 = ????
1
1
????
2
, Δф2 = ????
????
, Δф = .????
Δф = Δф1 + Δф2 = ????(
????1
+
????2
). Поэтому
1 Δф
= =???? ????
1
????1
1
+ .????2
Итак, при последовательном соединении конденсаторов суммируются обратные вели-чины емкостей. Еще раз подчеркну: это справедливо только, если полный заряд на каждой паресоединенныхмеждусобой обкладок конденсаторовравеннулю!
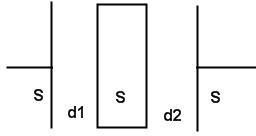
Пример А. Плоский конденсатор с пластинами площадью ????, расположенными на расстоянии ????O друг от друга, заряжен до разно- сти потенциалов фO. Какой станет разность потенциалов между об- кладками конденсатора, если в него внести металлическую незаря-женную пластину толщиной d и той же площади ?????
Решение. Емкость плоского конденсатора ????O
= ????????0. Следователь-
????0
????1
????2но, заряд на его обкладках ????O
= ????OфO
= ????????0 ф
O
????0
. После внесения пластины
???? ???? ???? ????
мы получаем батарею из двух последовательно соединенных конденсаторов, поэтому:
1 1
=???? ????1
1
+????2
????1
=????sO
????2
+????sO
????1 + ????2
=????sO
????O − ????
= .????sO
Откуда ѐмкость батареи ???? = ????????0 . Поскольку заряд
????0 − ????
батареи ????O, то искомая разность потенциалов:
????O
−????O
????OΔф =
????O
=
????sO
ф ????O
− ????
????O
=
????
− ???? −
ф . 21 ????
????O
O ????sO
????O O
???? ????
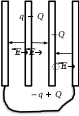
Пример Б. Пусть все будет как в примере А, но вне- сенная пластина заряжена зарядом Q.
Решение. В этом случае, пользуясь теоремой един- ственности, получаем, что заряды распределятся на про-
2 2
????1
1 2
водниках так, как показа на рисунке. Поэтому разность потенциалов между обкладками 1 и 2 бу- дет равна (пользуемся принципом суперпозиции):
Δф = ф1 − ф2 = ????1(????1 + ????2) + ????2(−????1 + ????2),
где ????
=????0, ????
= Q/2. Поскольку ????
= ????0 ф
, а ????
+ ????
= ????
− ????, то окончательно имеем:
1 ????????0 2
????????0
O ????0 O 1 2 O
????O−????
Δф = фO
????O
????
+2????sO
(????2
− ????1).