Файл: Лекция 4.docx

Энергия заряженного конденсатора. Плотность энергии электростатического поля

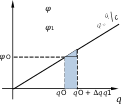
Чтобы зарядить конденсатор, необходимо перенести свободные заряды с одной пластины на другую. Электростатическое поле, возникающее при этом между пластинами, будет действо- вать на переносимые заряды, препятствуя процессу переноса, т.е. совершая отрицательную рабо- ту и увеличивая потенциальную энергию взаимодействия разделенных зарядов, то есть потенци- альную энергию конденсатора. Пусть обкладки конденсатора уже заряжены зарядами ????_O и −????_O (????_O 0). Пусть емкость конденсатора C, тогда разность потенциалов между его обкладками ф_O = ф₊ − ф₋ = ????_O/????. Следовательно, при переносе очень малого положительного заряда Δ???? с отрицательно заряженной обкладки на положительно заряженную обкладку, электрическое поле совершит работу Δ = − Δ????ф_O, а потенциальная энергия конденсатора увеличится на ΔW = Δ????ф_O. Если построить график зависимости разности потен-

циалов между обкладками конденсатора от величины его заряда q, то ΔW будет равно площади заштрихованной об- ласти под графиком (см. рисунок), умноженной на соответ- ствующий масштабный множитель. Отсюда ясно, что при перемещении с одной первоначально не заряженной пла- стины конденсатора емкости C на другую пластину некото- рого заряда ????₁, электрическое поле совершит работу

1 ????² ????ф²

= −

ф ???? = − ¹ = −¹,

₂ 1 1

2???? 2

а энергия конденсатора W изменится на величину

1 ^{????2 ????ф2}


1 1
ΔW = ???? ф =¹ =¹.

2 2???? 2

Полагая энергию незаряженного конденсатора равной нулю, получим, что энергия конденсатора емкости C, заряженного зарядом q до разности потенциалов ф равна

1

W = ????ф = 2

_????2


2????

????ф²

= .

2

С другой стороны, энергиюзаряженногоконденсатораможнорассматриватькакэнер-гиюэлектростатического поля, заключенногомеждуего обкладками.

Рассмотрим плоский конденсатор с пластинами площади S, расположенными на расстоя- нии d. Пусть пространство между пластинами заполнено диэлектриком с диэлектрической про-

А разность потенциалов между пластинами

???? =

.

????s_Os

ф = ????????.

Выражая из предпоследней формулы q через E и подставляя выражения для q и ф в фор- мулу для энергии заряженного конденсатора (и, следовательно, для энергии электростатического поля), получим:



_{W =} 1 1 <sub>2

2</sub> (????s_Os????)(????????) = ₂ s_Os???? ????

где ???? ???????? – объем области между обкладками конденсатора. Отсюда очевидно, что плотность энергии электрического поля, то есть его энергия в единице объема, определяется формулой:

1

???? = s



s????².