Файл: Понятие функции, основные свойства функции, классификация функций.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 16
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вариант 6
-
Понятие функции, основные свойства функции, классификация функций.
Если каждому элементу x множества X ставится в соответствие единственный элемент y множества Y, то говорят, что на множестве X задана функция y=f(x). При этом x называют независимой переменной или аргументом, а y – зависимой переменной или функцией, а f обозначает закон соответствия. Множество X называют областью определения функции, а множество Y – областью значений функции.
Существует несколько способов задания функций.
1) Аналитический способ – функция задается формулой вида y=f(x).
2) Табличный способ – функция задается таблицей, содержащей значения аргумента x и соответствующие им значения функции y=f(x).
3) Графический способ – изображение графика функции, т.е. множества точек (x; y) координатной плоскости, абсциссы которых представляют значения аргумента x, а ординаты – соответствующие им значения функции y=f(x).
4) Словесный способ – функция описывается правилом ее составления. Например, функция Дирихле f(x) принимает значение 1, если x – рациональное число и 0, если x – иррациональное число.
Выделяют следующие основные свойства функций.
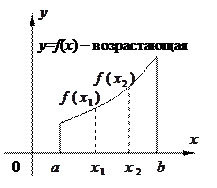
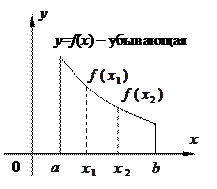
1 Четность и нечетность. Функция y=f(x) называется четной, если для любых значений x из области ее определения выполняется f(–x)=f(x), и нечетной, если f(–x)=–f(x). Если не выполняется ни одно из перечисленных равенств, то y=f(x) называется функцией общего вида. График четной функции симметричен относительно оси Oy, а график нечетной функции симметричен относительно начала координат.
2 Монотонность. Функция y=f(x) называется возрастающей (убывающей) на промежутке X, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции. Пусть x1,x2
∈X, x2>x1. Тогда функция возрастает на промежутке X, если f(x2)>f(x1), и убывает, если f(x2)<f(x1).
Наряду с возрастающими и убывающими функциями рассматривают неубывающие и невозрастающие функции. Функция называется неубывающей (невозрастающей), если при x1,x2∈X, x2>x1 выполняется неравенство f(x2)≥f(x1) (f(x2)≤f(x1)).
Возрастающие и убывающие функции, а также невозрастающие и неубывающие функции называют монотонными.
3 Ограниченность. Функция y=f(x) называется ограниченной на промежутке X, если существует такое положительное число M>0, что |f(x)|≤M для любого x∈X. В противном случае функция называется неограниченной на X.
4 Периодичность. Функция y=f(x) называется периодической с периодом T≠0, если для любых x из области определения функции f(x+T)=f(x). В дальнейшем под периодом будем понимать наименьший положительный период функции.
Функция называется явной, если она задана формулой вида y=f(x). Если функция задана уравнением F(x, y)=0, не разрешенным относительно зависимой переменной y, то ее называют неявной.
Пусть y=f(x) есть функция от независимой переменной x, определенная на множестве X с областью значений Y. Поставим в соответствие каждому y∈Y единственное значение x∈X, при котором f(x)=y. Тогда полученная функция x=φ(y), определенная на множестве Y с областью значений X, называется обратной и обозначается y=f–1(x). Графики взаимно обратных функций симметричны относительно биссектрисы первой и третьей координатных четвертей y=x.
Пусть функция y=f(u) есть функция переменной u, определенной на множестве U с областью значений Y, а переменная u в свою очередь является функцией u=φ(x), определенной на множестве X с областью значений U. Тогда заданная на множестве X функция y=f(φ(x)) называется сложной функцией (композицией функций, суперпозицией функций, функцией от функции).
Элементарные функции
К основным элементарным функциям относят:
-
степенную функцию y=xn; y=x–n и y=x1/n; -
показательную функцию y=ax; -
логарифмическую функцию y=logax; -
тригонометрические функции y=sin x, y=cos x, y=tg x и y=ctg x; -
обратные тригонометрические функции y= arcsin x, y=arccos x, y=arctg x и y=arcctg x.
Из основных элементарных функций новые функции могут быть получены при помощи алгебраических действий и суперпозицией функций.
-
Определить, при каких значениях m и n две прямые: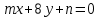 ,
, 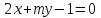 : 1) параллельны, 2) совпадают, 3) перпендикулярны.
: 1) параллельны, 2) совпадают, 3) перпендикулярны.
Решение.
-
Прямые, заданные общими уравнениями: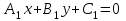 и
и 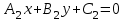 параллельны тогда и только тогда, когда
параллельны тогда и только тогда, когда 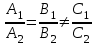 .
.
Получаем, что наши прямые
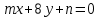 и
и 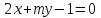 параллельны при условии
параллельны при условии 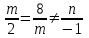 , т.е.
, т.е. 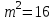 ,
, 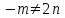 .
.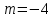 ,
, 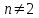 , например,
, например, 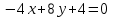 и
и 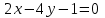 ;
;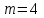 ,
, 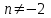 , например,
, например, 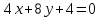 и
и 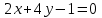 .
.-
Прямые, заданные общими уравнениями: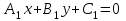 и
и 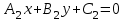 совпадают тогда и только тогда, когда
совпадают тогда и только тогда, когда 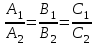 .
.
Получаем, что наши прямые
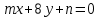 и
и 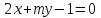 совпадают при условии
совпадают при условии 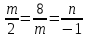
, т.е.
 ,
, 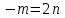 .
. ,
, 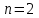 , т.е.
, т.е. 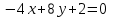 и
и  ;
; ,
, 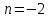 , т.е.
, т.е. 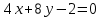 и
и  .
.-
Прямые, заданные общими уравнениями: и
и  взаимно перпендикулярны тогда и только тогда, когда
взаимно перпендикулярны тогда и только тогда, когда 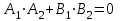 .
.
Получаем, что наши прямые
 и
и  взаимно перпендикулярны при условии
взаимно перпендикулярны при условии 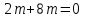 , т.е.
, т.е. 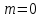 .
.Например:
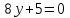 и
и 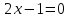 .
.-
Установить, что каждое из следующих уравнений определяет гиперболу. Найти ее центр, полуоси, эксцентриситет, уравнения директрис и асимптот, изобразить гиперболу на координатной плоскости.
-
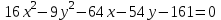 ,
, -
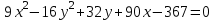 ,
, -
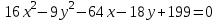 .
.
Решение.
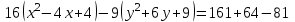
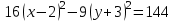
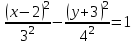 ̶ каноническое уравнение гиперболы.
̶ каноническое уравнение гиперболы.Ее центр: О(2;-3).
Полуоси:
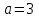 ;
; 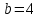
Эксцентриситет:
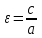 .
. 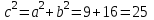 .
. 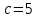 .
.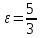
Уравнения директрис: d1:
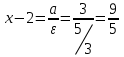 ;
; 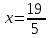
d2:
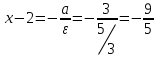 ;
; 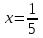
Уравнения асимптот:
a1:
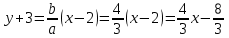 ;
; 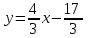
a2:
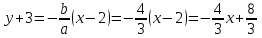 ;
; 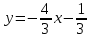
Изобразим гиперболу на координатной плоскости:
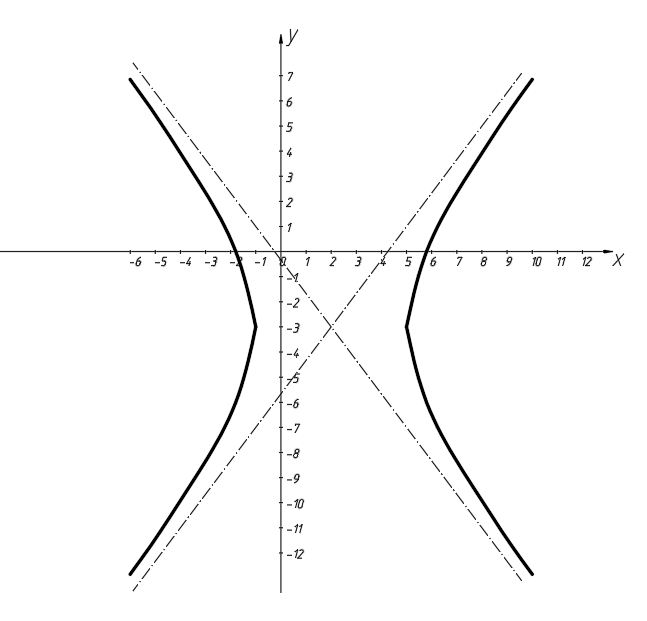
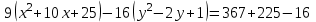
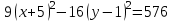
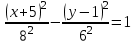 ̶ каноническое уравнение гиперболы.
̶ каноническое уравнение гиперболы.Ее центр: О(-5; 1).
Полуоси:
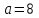 ;
; 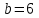
Эксцентриситет:
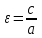 .
. 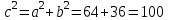 .
. 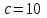 .
.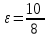
Уравнения директрис: d1:
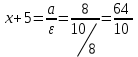 ;
; 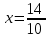
d2:
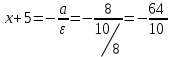 ;
; 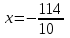
Уравнения асимптот:
a1:
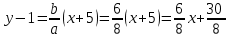 ;
; 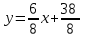
a2: