ОТЧЕТ

По расчетно-графической работе ид практики

на тему:

«Основы гидроупругости и аналитической гидромеханики»

Нижний Новгород
2022 г.

Содержание

1. 
   Постановка задачи……………………………………………………………… 3
   
2. 
   Решение…………………………………………………………………………. 4
   

Постановка задачи

Уравнение поперечных колебаний трубопровода с постоянным потоком несжимаемой жидкости имеет вид:

,

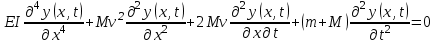где EI – изгибная жесткость трубопровода, m – распределенная масса трубопровода, M – распределенная масса жидкости.

Оба конца трубопровода жестко закреплены: 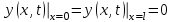, 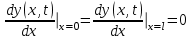(l – длина трубопровода).

Поставить задачу проблемы нахождения собственных значений и собственных форм деформации для упрощенной задачи в случае отсутствия движения жидкости. Найти первые три собственных значения и соответствующие им формы деформации.

Найти первые три формы деформации в полиномиальном виде (пример выполнения https://e-learning.unn.ru/mod/page/view.php?id=223843 ) из условий согласования с граничными условиями и условиями ортонормированности форм и построить их график. Провести сравнительный анализ этих форм с формами, полученными из задачи на проблему собственных значений, используя метод среднего квадратичного отклонения в n узловых точках (n=1000).

Для наглядности соответствующие формы деформации, полученные разными подходами, должны быть изображены на одном графике.

Проверить операторы задачи на самосопряженность и положительноопределенность.

Найти критическое значение скорости потока жидкости, при которой происходит потеря устойчивости (методом Бубнова-Галеркина).

Решение

1. 
   Проверка на самосопряженность
   

Матричный оператор:



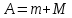
Оператор демпфирования:

---

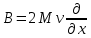
Оператор жесткости:


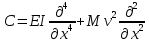
Так как оператор А выражен константами, то условие самосопряженности выполняется автоматически:



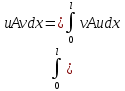
Проверим на самосопряженность оператор В с помощью условия:



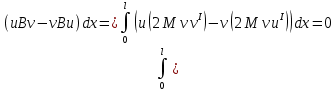
Интегрирование по частям слагаемых:



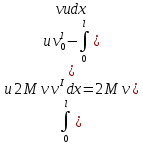
В случае, когда оба конца трубопровода жестко закреплены оба слагаемые обращаются в нуль за счет обращения в нуль Y и первых производных от функций сравнения. Отсюда следует, что В – не самосопряженное.

Проверим на самосопряженность оператор C с помощью условия:





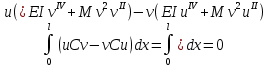
Интегрирование по частям слагаемых:






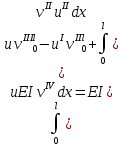
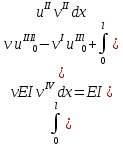
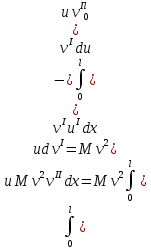
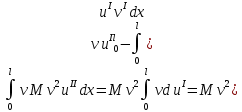
Тогда получаем:

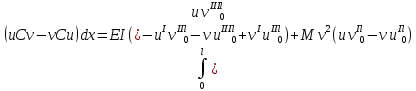
В случае закрепления, когда оба конца трубопровода жестко закреплены, первое и третье слагаемые обращаются в нуль за счет обращения в нуль Y и третьих производных от функций сравнения. Второе и четвертое слагаемые обращаются в нуль за счет обращения в нуль первых и вторых производных от функций сравнения. Пятое и шестое слагаемые обращаются в нуль за счет обращения в нуль Y и первых производных от функции сравнения. Отсюда следует, что С – самосопряженное.

Проведем проверку положительности операторов.



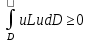
В случае оператора А для функции сравнения u имеем:



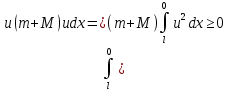
то есть оператор А положительный.

В случае оператора В имеем:


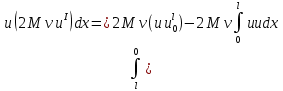
тогда видно, что из-за последнего слагаемого в общем случае оператор В не является положительным.
В случае оператора С имеем:

---

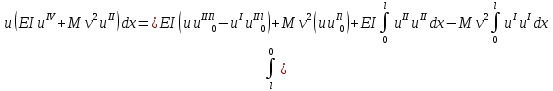
тогда видно, что из-за последних двух слагаемых в общем случае оператор С не является положительным.

2. 
   Проблема собственных значений
   

Уравнение движения трубопровода имеет вид:

. (*)

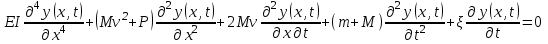Запись задачи в безразмерном виде:

Поделив уравнение (*) на 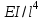и проведя замену переменных 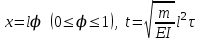, получим уравнение движения в безразмерных параметрах:

.

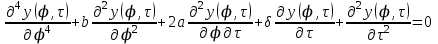Здесь , , .

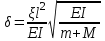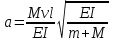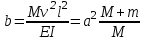Для постановки задачи на проблему собственных значений рассмотрим случай отсутствия движения жидкости по трубопроводу, сжимающей нагрузки и потерь на трение. Тогда уравнение примет вид:

.

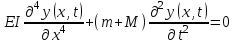Переобозначим параметр, отвечающий за общую массу:

.

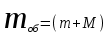В этом случае решение задачи на проблему собственных значений будет идентичен случаю сжатого стержня.
Замена переменных:








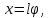
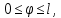
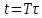
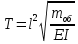
Уравнение движения в безразмерном виде:

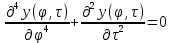
Граничные условия:


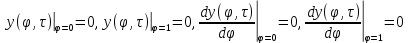
Подставим решение в виде:





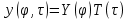
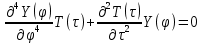
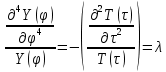
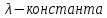
Задача на проблему собственных значений:

---

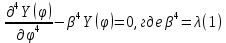
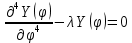
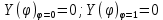
(2)


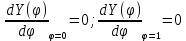
Задача для определения зависимости от времени поведения собственных мод деформаций:

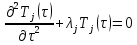
Ищем решение задачи (1)-(2) в виде:



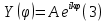
После подстановки (3) в уравнение (1) для нахождения собственных значений 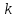получим: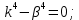



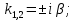
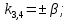
Используя формулы Эйлера, общее решение (3) преобразуется:

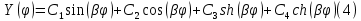
Для нахождения коэффициентов 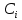(i=1,2,3,4) выражения (4) используем краевые условия (2):

Получим систему:


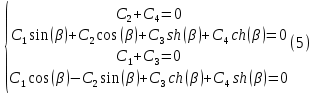
Получили систему линейных алгебраических однородных уравнений, для нетривиального решения которой необходимо обращение в 0 ее определителя.

Вычислим его:


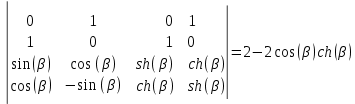
В итоге получаем:



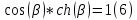
Численно решая (6) получаем:

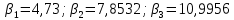
Найдем коэффициенты 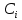для 1 случая: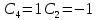








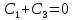
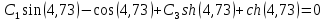
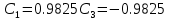
Тогда

---

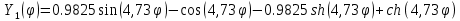
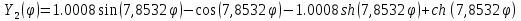
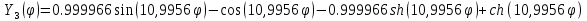
Для приведения форм к нормированному виду найдем нормирующий множитель 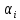из условия нормированности форм: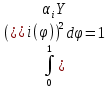


Получаем:







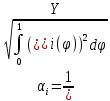
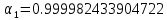
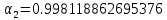
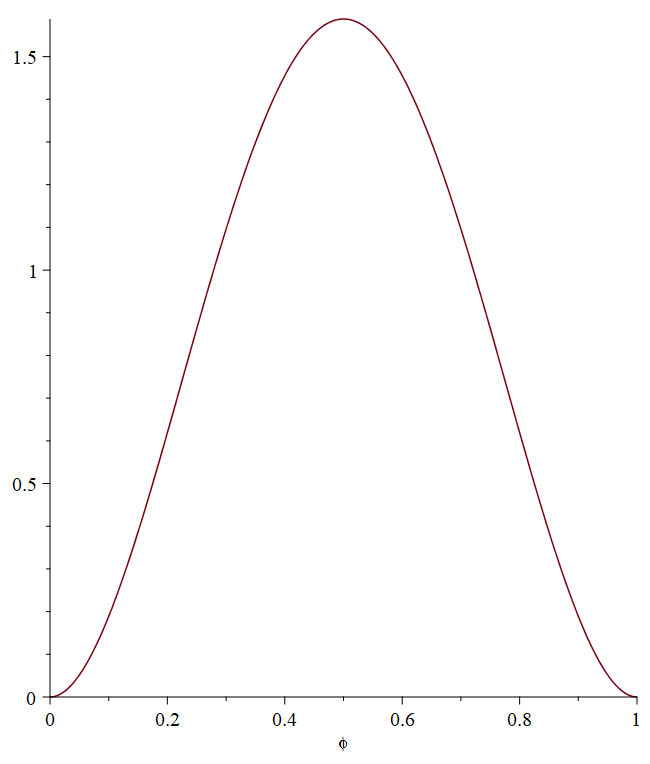
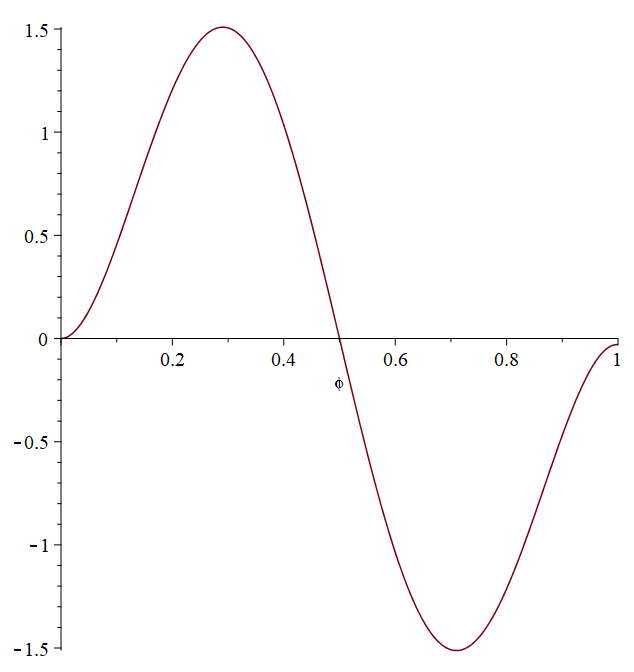
Тогда нормированные формы примут вид:









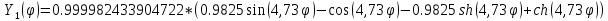
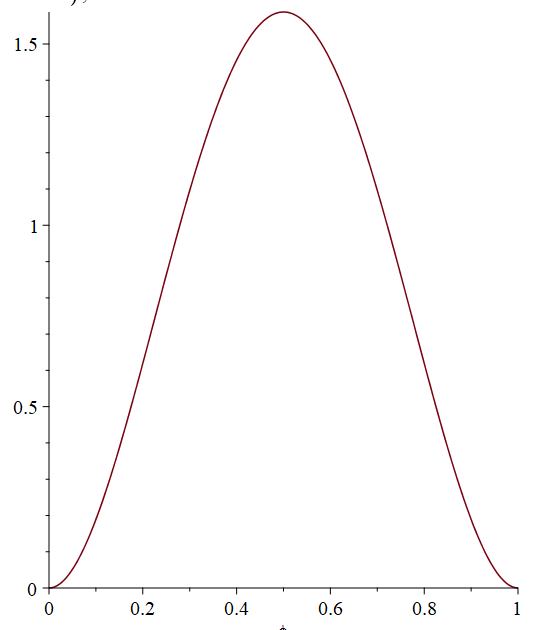
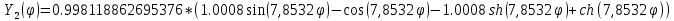
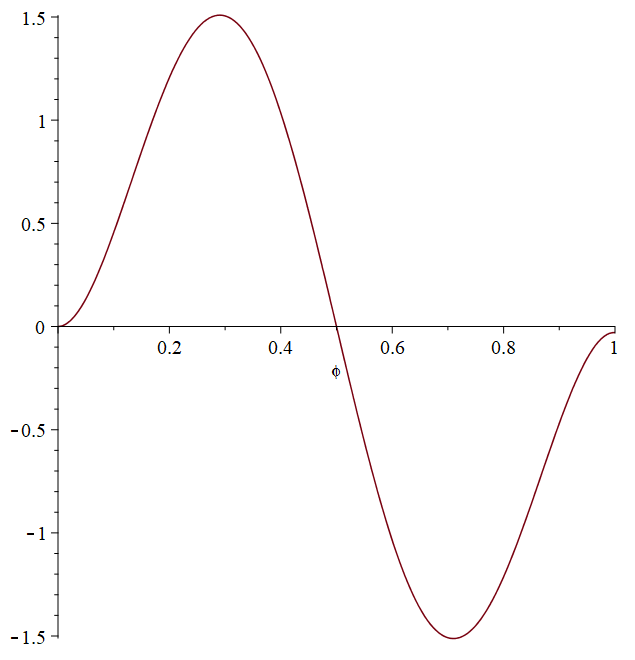
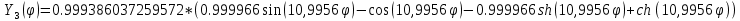
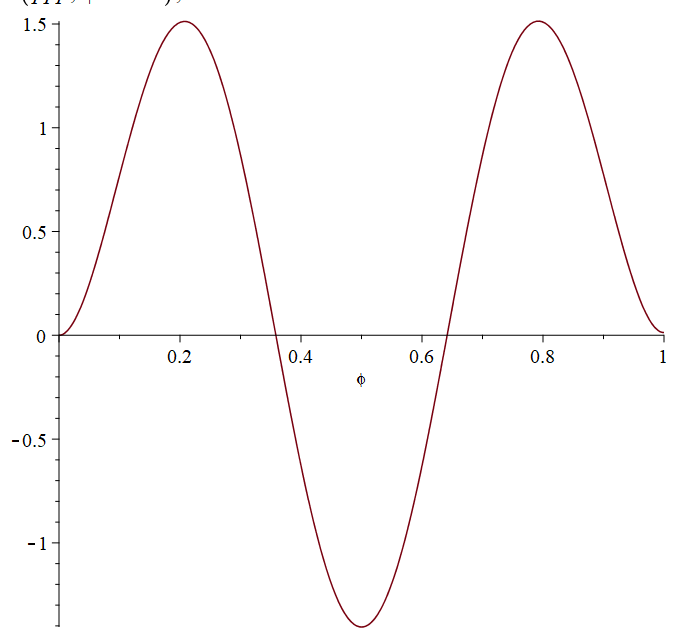
Найдем функции сравнения в полиномиальном виде. Будем искать набор из трех полиномов, удовлетворяющих граничным условиям и обладающих свойством ортонормированности. Полиномы должны иметь степень не ниже четвертой.

Для нахождения коэффициентов полиномов будем решать систему, полученную из граничных условий и условий ортонормированности:



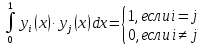
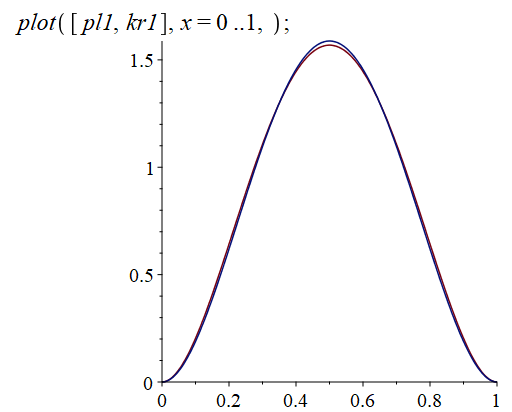
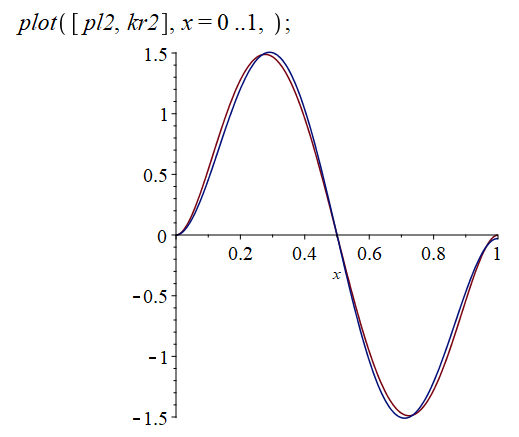
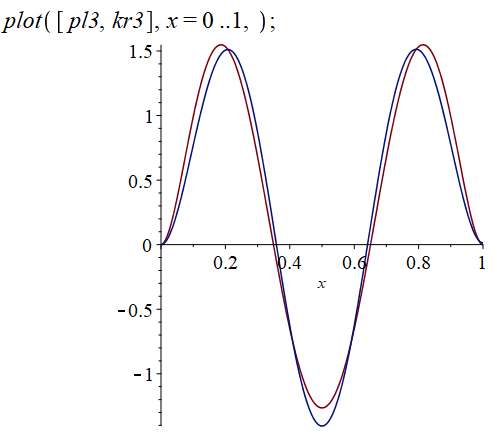
В итоге получаем следующие уравнения для первых трех форм в полиномиальном виде:







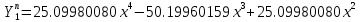
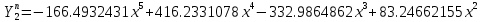
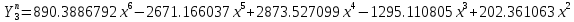
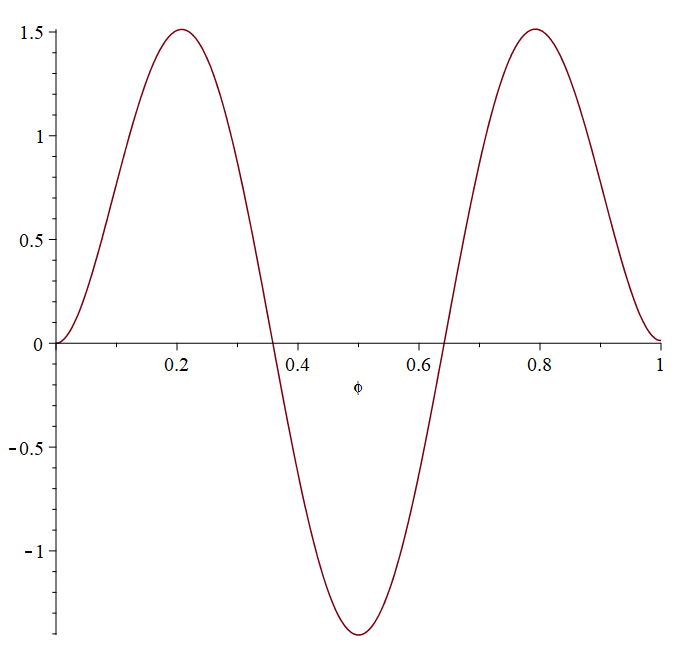
Ниже представлены графики для наглядного сравнения полученных полиномов с соответствующими тремя нормированными функциями Крылова. (Красный – полиномы, синий – функции Крылова)







Для того, чтобы оценить отличие форм

---

Смотрите также файлы

• Постовой на посту безопасности гдзс при осуществлении своей деятельности обязан.docx

• Курсовая работа по учебной дисциплине Теоретические основы товароведения (в отрасли) на тему Классификация ассортимента товаров.doc

• Особенности проведения маркетинговых исследований в сети Интернет.docx

• псп. Отработка норматива по гдзс 8.doc

• Контрольная работа 1 по дисциплине Бухгалтерский управленческий учет Студент гр спец,060505 (080109) Тютрина Т. В. Тютрина.doc