Файл: Основы гидроупругости и аналитической гидромеханики.docx
Добавлен: 07.11.2023
Просмотров: 20
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, полученных при помощи полиномов, от форм, полученных при помощи функций Крылова, посчитаем среднее квадратичное отклонение:
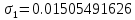
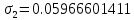
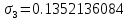
Наше уравнение, описывающее колебания нашего стержня в безразмерном виде:
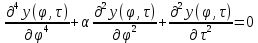
Где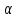
– нагрузка.
Решение задачи будем искать в следующем виде: где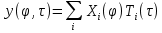
– полная система ортонормированных базисных функций.
Проведем стандартную процедуру метода Бубнова-Галеркина с учетом условий ортонормированности. Представив общее решение в виде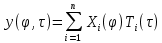
, подставим его в уравнение движения системы:
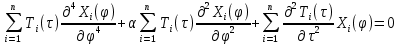
Поочередно умножив полученное выражение на набор базисных функций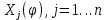
и проитегрировав по координате 
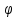, получим систему уравнений:
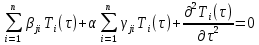
Где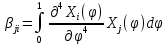
и 
, 
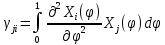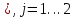
В случае двухмодового приближения получаем систему:
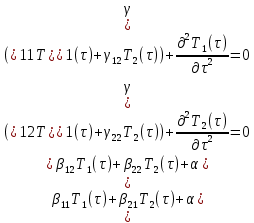
Запишем для нее характеристическое выражение:
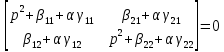
В итоге характеристическое выражение имеет вид:
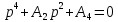
Где
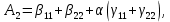
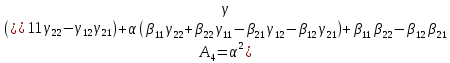
При использовании критерия Рауса-Гурвица обращаются в нули детерминанты. Полученное при проводимом в настоящей работе исследовании при нулевом трении значение критической нагрузки соответствует границе «квазиустойчивости» и требует проверки.
Квадраты корней характеристического уравнения имеют вид:
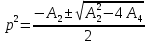
Потеря устойчивости происходит в одном из двух случаев:
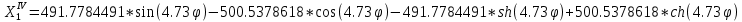
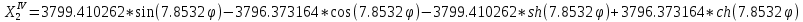
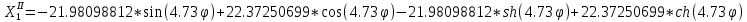
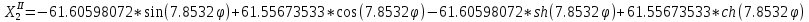
Отсюда:
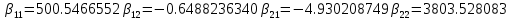
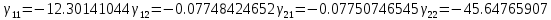
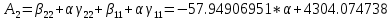
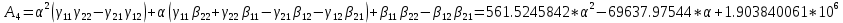
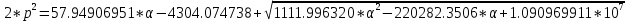
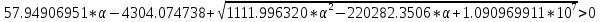
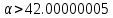
Невозможен, так как при любых α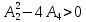
;
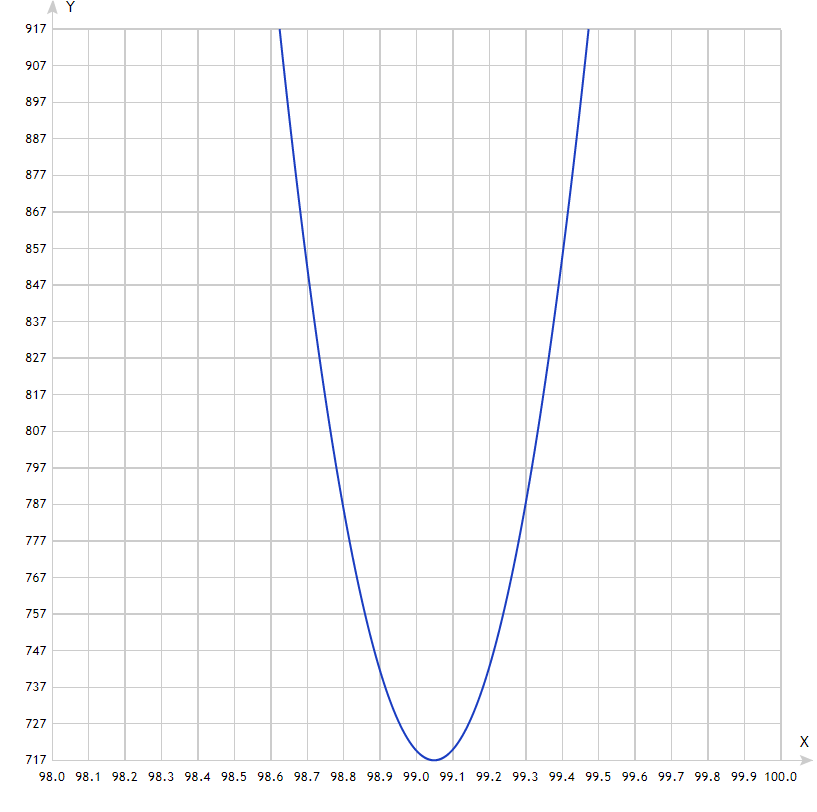
Система устойчива при
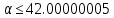
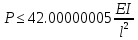
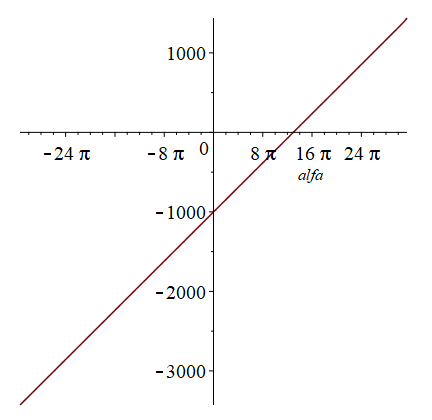
Ф. Крылова
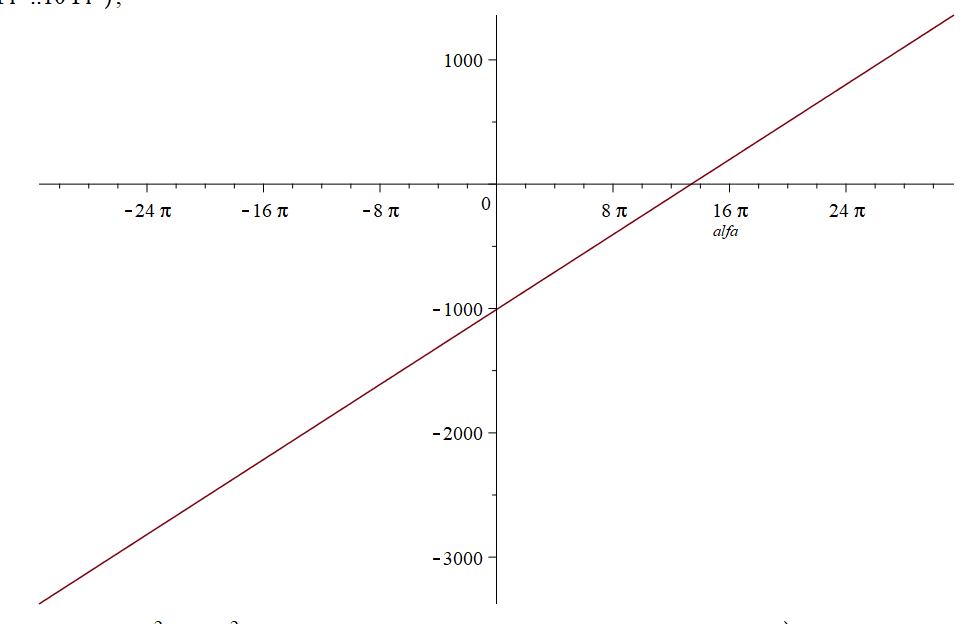
Полином
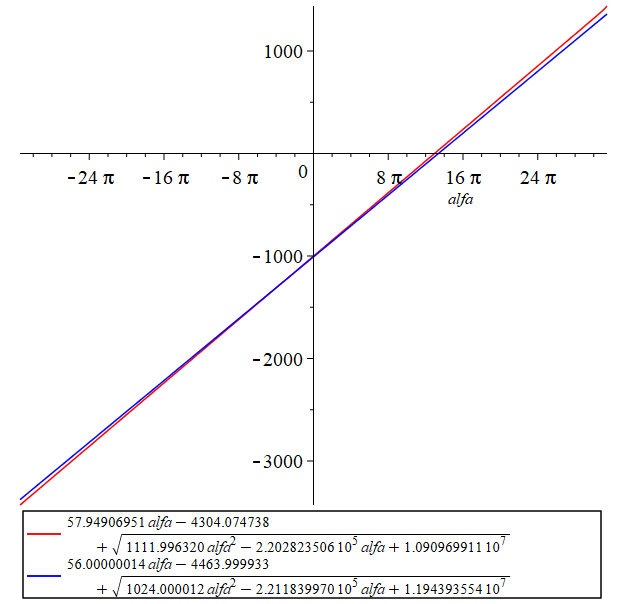
Сравнение
-
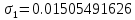
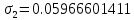
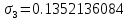
Проблема собственных значений
Наше уравнение, описывающее колебания нашего стержня в безразмерном виде:
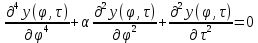
Где
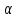– нагрузка.Решение задачи будем искать в следующем виде: где
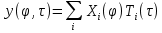– полная система ортонормированных базисных функций.Проведем стандартную процедуру метода Бубнова-Галеркина с учетом условий ортонормированности. Представив общее решение в виде
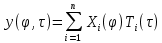, подставим его в уравнение движения системы: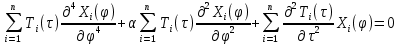 Поочередно умножив полученное выражение на набор базисных функций
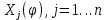и проитегрировав по координате 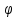, получим систему уравнений: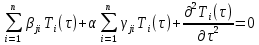 Где
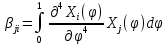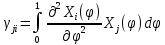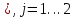
и , В случае двухмодового приближения получаем систему:
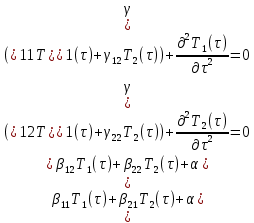
Запишем для нее характеристическое выражение:
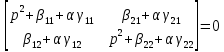
В итоге характеристическое выражение имеет вид:
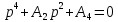
Где
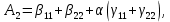
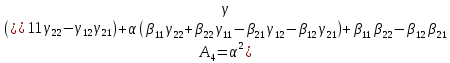
При использовании критерия Рауса-Гурвица обращаются в нули детерминанты. Полученное при проводимом в настоящей работе исследовании при нулевом трении значение критической нагрузки соответствует границе «квазиустойчивости» и требует проверки.
Квадраты корней характеристического уравнения имеют вид:
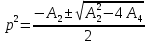
Потеря устойчивости происходит в одном из двух случаев:
-
Числитель имеет действительное значение, и при этом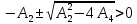
-
Числитель имеет комплексную часть, то есть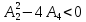
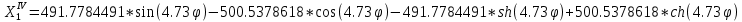
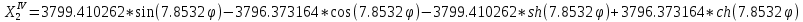
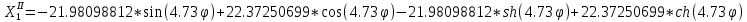
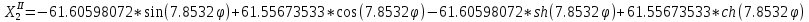
Отсюда:
-
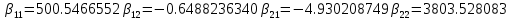
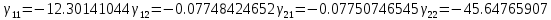
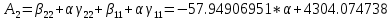
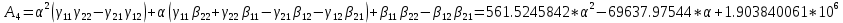
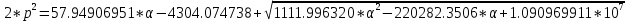
Числитель имеет действительное значение, и при этом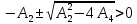
-
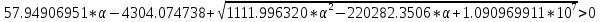
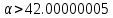
Числитель имеет комплексную часть, то есть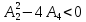
Невозможен, так как при любых α
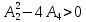; Система устойчива при
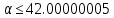
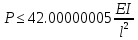
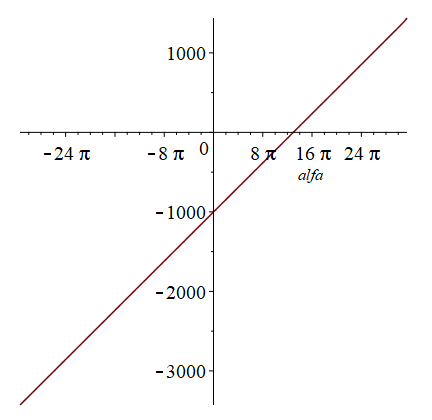
Ф. Крылова
Полином
Сравнение