Файл: Контрольная работа Образец выполнения контрольной работы 1.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.11.2023
Просмотров: 40
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Контрольная работа № 4.
Образец выполнения контрольной работы № 1.
Задание 1. Найти пределы числовых последовательностей, или установить их расходимость:
1.1.
Решение:
Данную последовательность можно представить как произведение ограниченной последовательности
, предел которой не определён, и сходящейся последовательности 
, предел которой равен нулю. Согласно одному из свойств сходящихся последовательностей, произведение ограниченной и сходящейся последовательности есть также сходящаяся последовательность, предел которой равен пределу последней. Тогда:
.1.2.
.Решение:
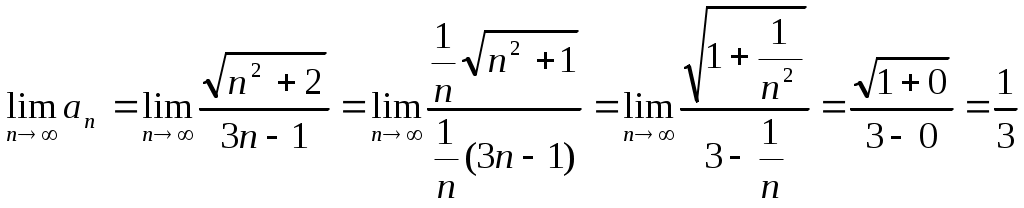.1.3.
.Решение:
Как и в первом пункте данного задания, представим данную последовательность в виде произведения двух последовательностей:
, где 
. Очевидно, 
. Последовательность 
в силу свойств косинуса является ограниченной: 
. Таким образом, члены последовательности 
при 
будут принимать как неограниченно большие, так и неограниченно малые значения. Следовательно, данная последовательность является расходящейся и предел её не определён.
Задание 2. Найти пределы функций:
2.1.
.Решение:
В данном случае имеем неопределённость вида
. Для её раскрытия используем следующее известное свойство. Пусть дана дробно-рациональная функция
, где 
некоторые многочлены. Тогда:-
Если степень многочлена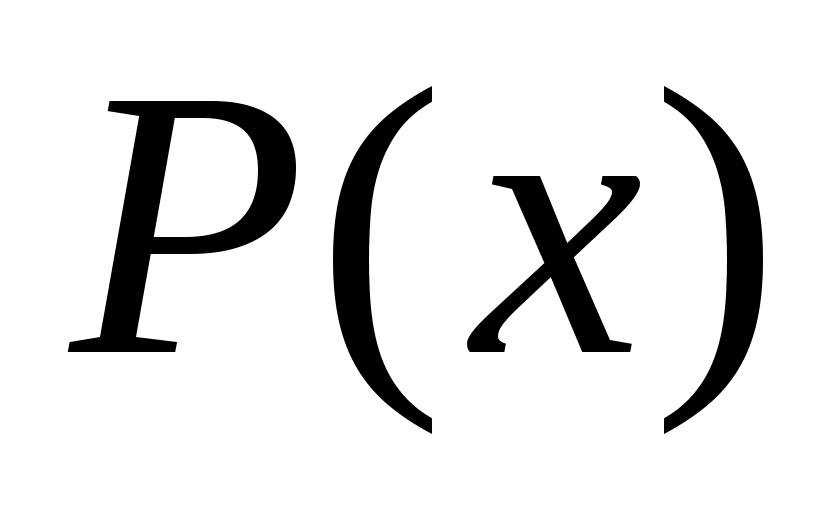
больше степени многочлена 
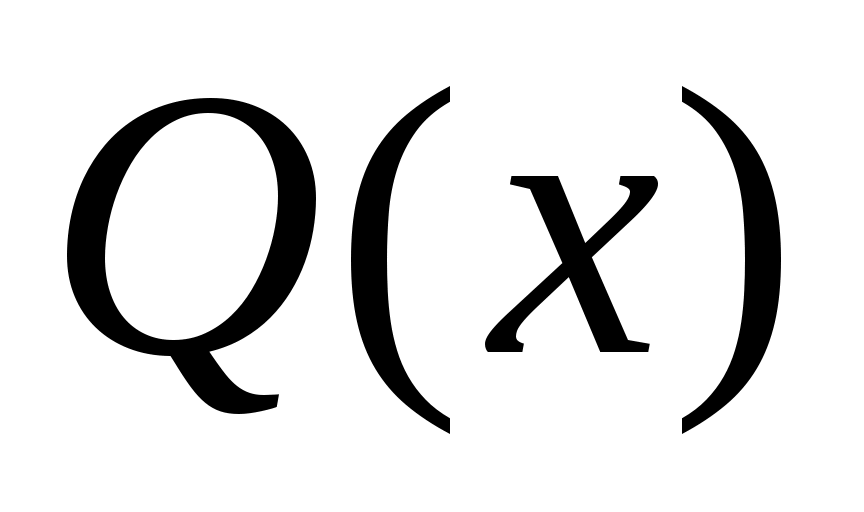, то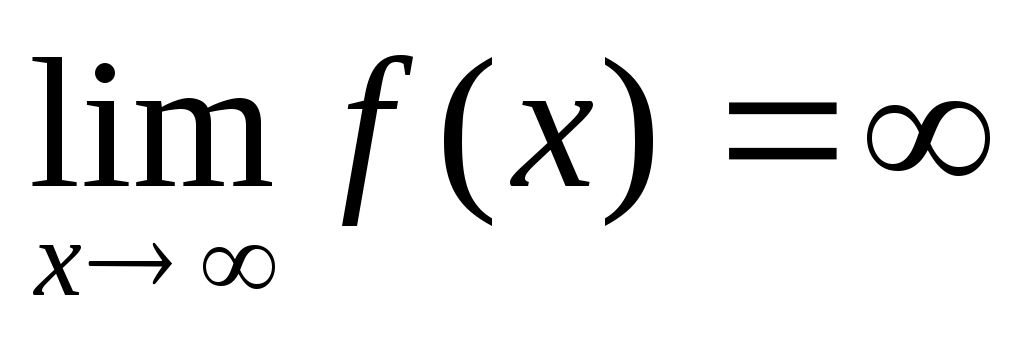 
. -
Если степень многочлена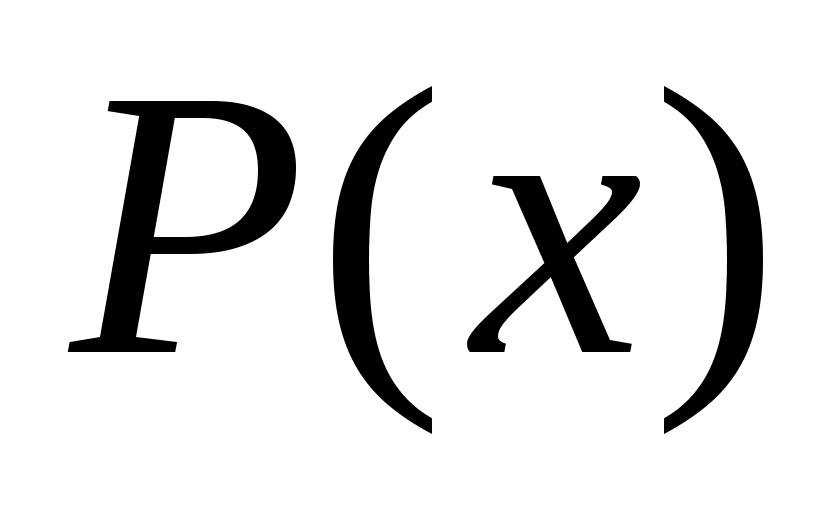 меньше степени многочлена 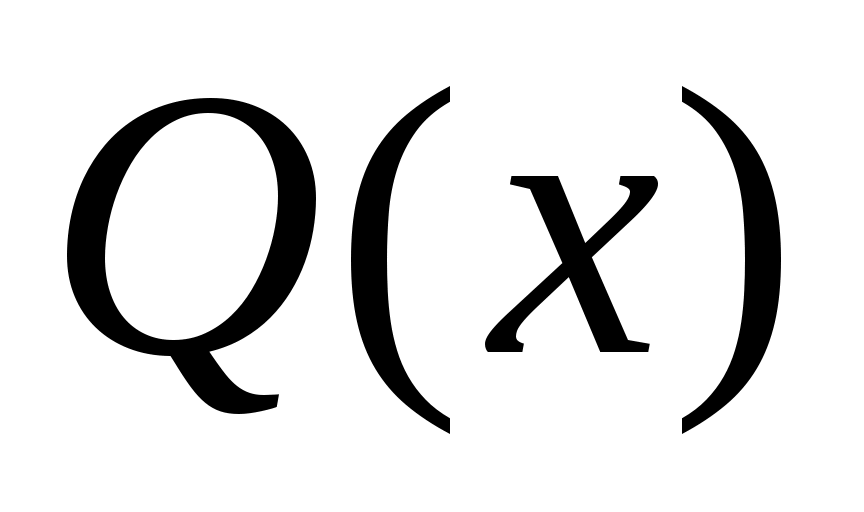, то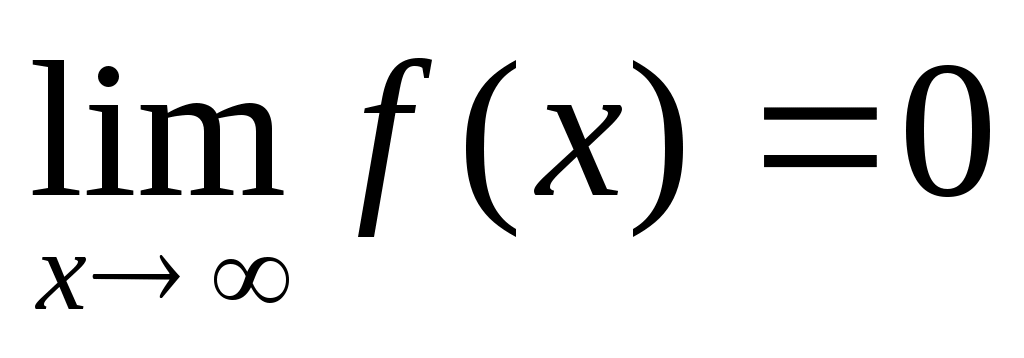 
. -
Если степень многочлена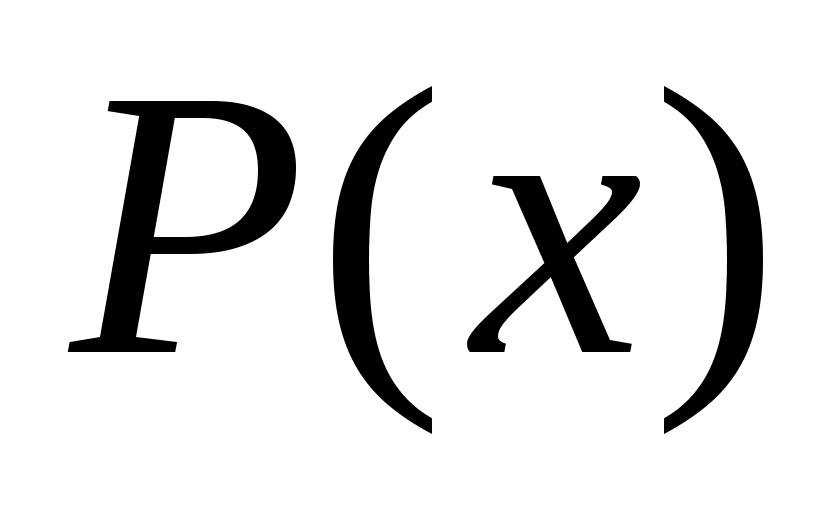 равна степени многочлена 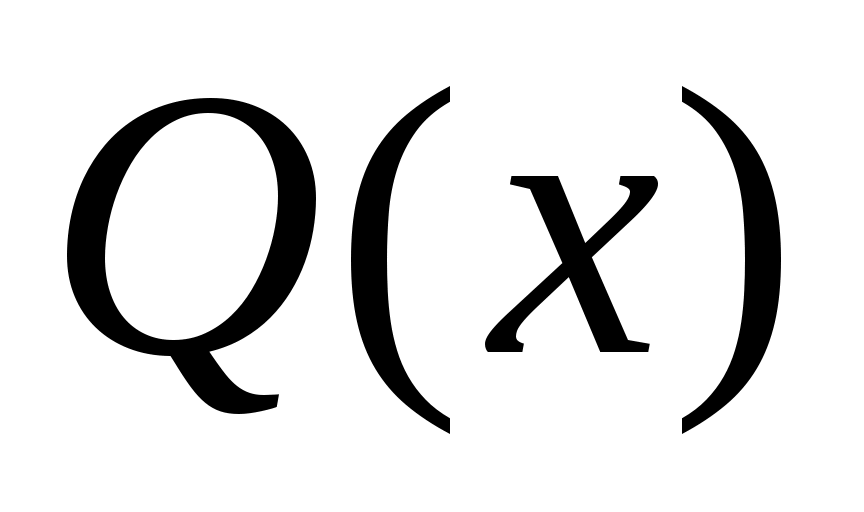, то 
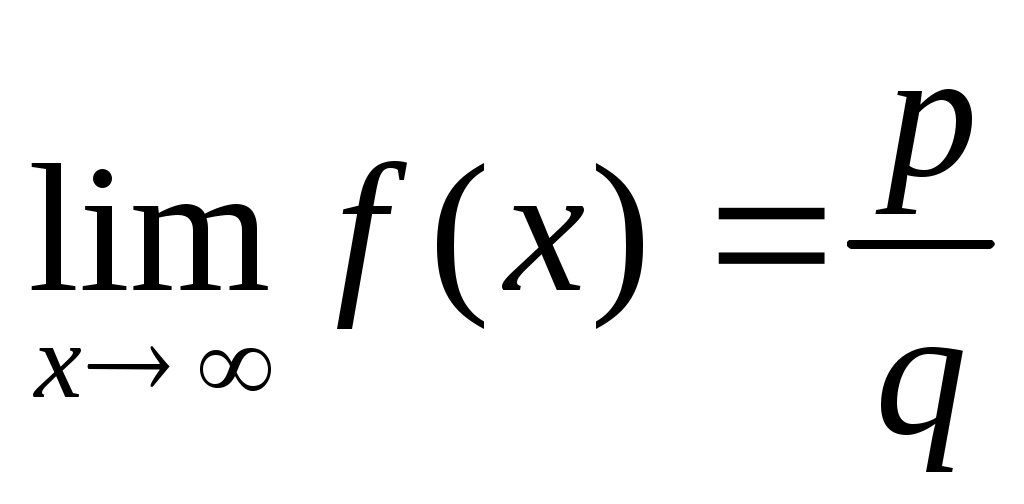, где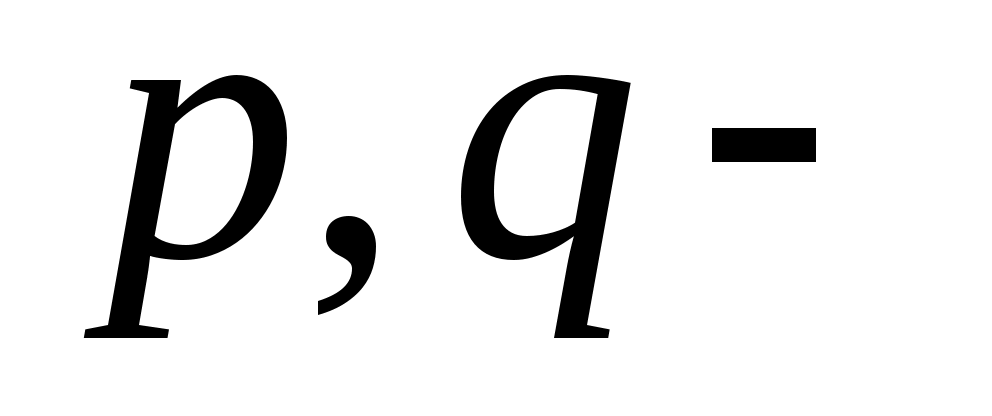 
числовые коэффициенты при наивысших степенях 
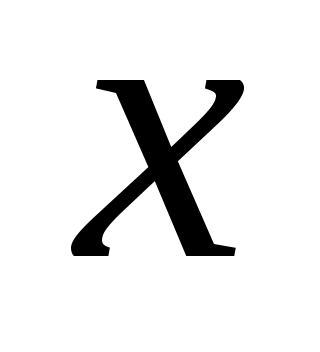в данных многочленах.
В данном случае степени числителя и знаменателя равны двум, поэтому
.2.2.
. Решение:
В данном случае снова имеем неопределённость вида
. Для её раскрытия используем то же известное свойство, что и в предыдущем случае. Степень числителя равна двум, а степень знаменателя – трём. Поэтому 
.2.3.
.
Решение:
В данном случае снова имеем неопределённость вида
. Чтобы раскрыть её, преобразуем данную функцию, предварительно разложив на множители числитель и знаменатель: 
.2.4.
.Решение:
В данном случае имеем неопределённость вида
. Чтобы раскрыть её, домножим данную дробь на дробь, сопряжённую её знаменателю: 
.2.5.
.Решение:
В данном случае имеем неопределённость вида
. Чтобы раскрыть её, введём подстановку 
. Заметим, что 
, при 
. Получим:
.2.6.
.Решение:
Имеем неопределённость вида
. Чтобы раскрыть её, приведём данную дробь к виду, который допускал бы применение первого замечательного предела 
.
.Замечание. При выполнении этого задания и заданий, подобных ему, можно использовать и другие способы решения – например, применить правило Лопиталя или эквивалентность бесконечно малых функций.
2.7.
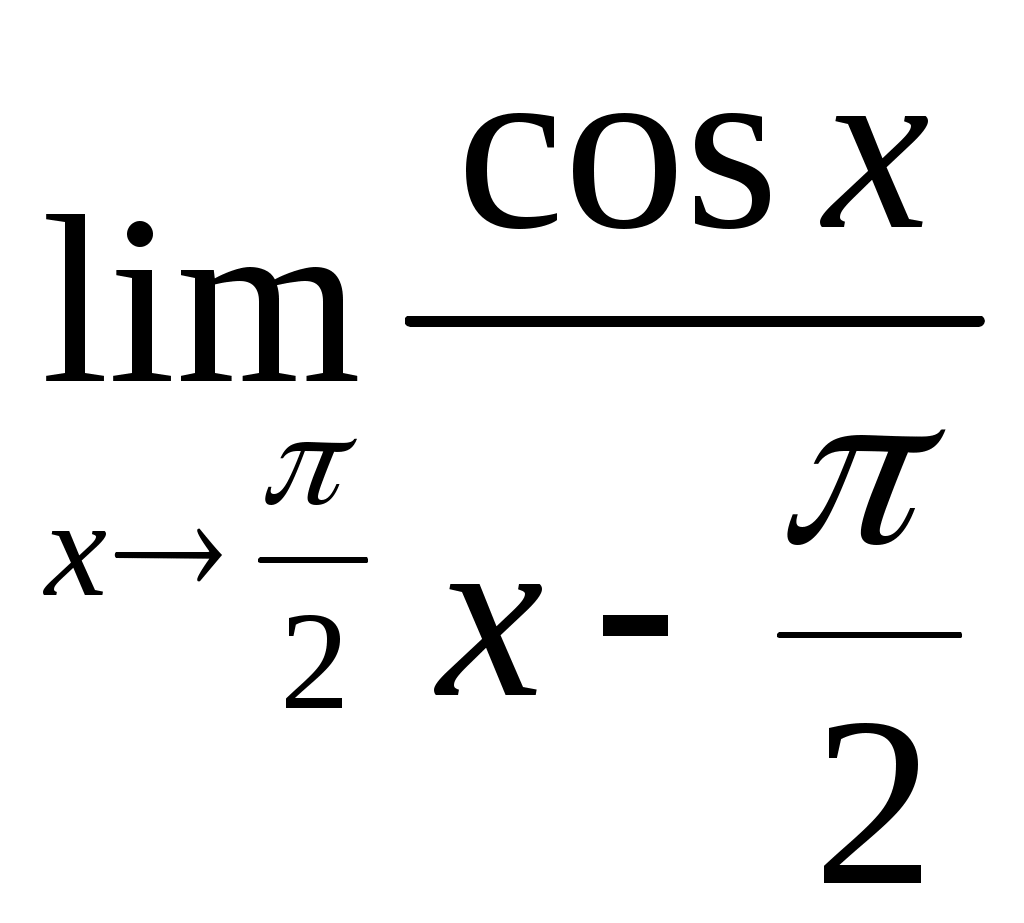.Решение:
Имеем неопределённость вида
. Чтобы раскрыть её, как и в предыдущем задании, приведём данную дробь к виду, который допускал бы применение первого замечательного предела
. Введём подстановку 
. Заметим, что 
, при 
. Получим:
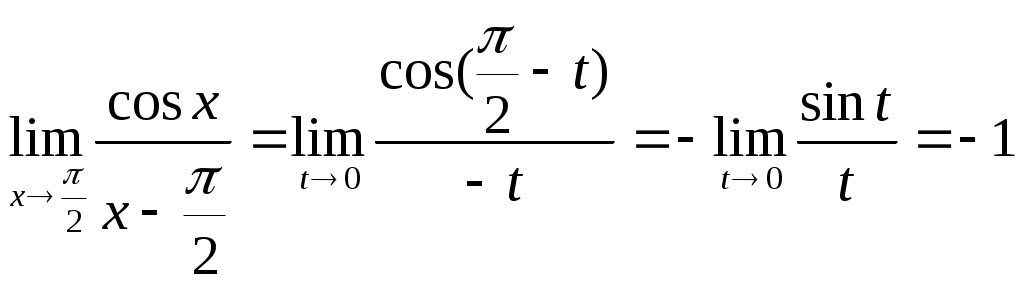.2.8.
.Решение:
Имеем неопределённость вида
. Чтобы раскрыть её, приведём данную дробь к виду, который допускал бы применение второго замечательного предела 
.
. Далее, воспользовавшись равенствами 
и 
, получим: 
.2.9.
.Решение:
Обратим внимание, что в данном случае
, поэтому нет необходимости использовать второй замечательный предел, поскольку нет никакой неопределённости, и предел может быть вычислен непосредственно.
.2.10.
.Решение:
Прежде всего, заметим, что если
стремится к единице слева, то 
будет принимать близкие к нулю отрицательные значения, и выражение 
, очевидно, стремится к
. Тогда: 
.Задание 3. Исследовать функцию на непрерывность:
.Решение:
Найдём область определения данной функции.
. Итак, имеем две точки разрыва: 
и 
. Теперь определим, каков характер разрыва функции в каждой из этих точек.Точка
является точкой бесконечного разрыва (второго рода), так как: 
.Точка
является точкой устранимого разрыва, так как:
.Окончательный ответ: функция непрерывна при
; точка является точкой бесконечного разрыва; точка является точкой устранимого разрыва и 
.