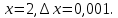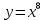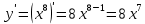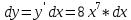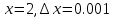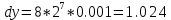Файл: Контрольная работа по дисциплине Математика вариант Студент гр з432П52 В. Н. Ветютнев Направления подготовки.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 14
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ
Федеральное государственное бюджетное образовательное
учреждение высшего образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
КОНТРОЛЬНАЯ РАБОТА
по дисциплине «Математика»
вариант 4.
Студент гр. з-432П5-2
В. Н. Ветютнев
Направления подготовки
09.03.01
«11» марта 2023 г.
Руководитель:
канд. физико-математических наук,
доцент кафедры Математики
О. В. Васильева
« » 20 г.
Задание1. Найдите производные от данных функций:
а)
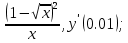
Производная частного равна производной числителя, умноженного на знаменатель минус числитель, умноженный на производную знаменателя и все это деленное на квадрат знаменателя.
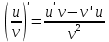
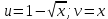
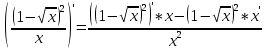
По таблице производных:
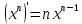
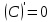
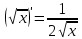
Производная от сложной функции:
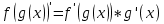
Отсюда.
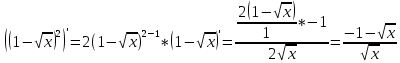
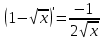
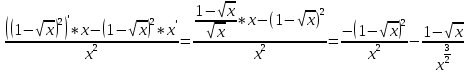
Ответ:
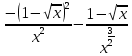
б)
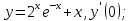
Производная произведения равна произведению производной первого множителя на второй плюс первый множитель, умноженный на производную второго.
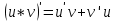
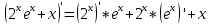
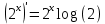
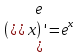
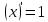
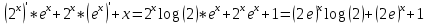
Ответ:
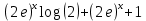
в)
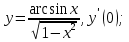
Производная частного равна производной числителя, умноженного на знаменатель минус числитель, умноженный на производную знаменателя и все это деленное на квадрат знаменателя.
По таблице производных:
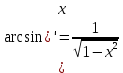
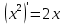
Производная от сложной функции:
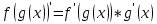
Отсюда.
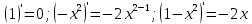
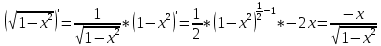
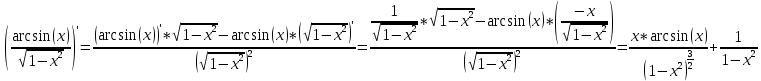
Ответ:
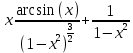
Задание 2. Дана функция
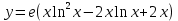. Найдите 
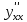. Вычислите 
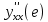.Производная произведения константы на функцию, есть произведение этой константы на производную этой функции.
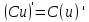
Производная от сложной функции:
Дифференцируем
.
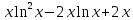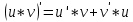
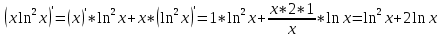
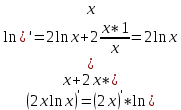
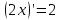
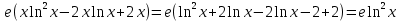
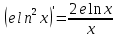
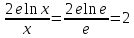
Ответ:
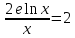
Задание 3. Дана функция
. Найдите 
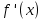и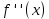 
. Вычислите 
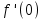и 
.
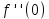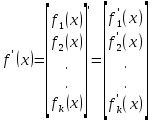
Находим первую производную частного
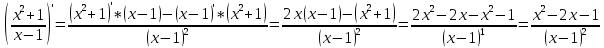
Находим вторую производную
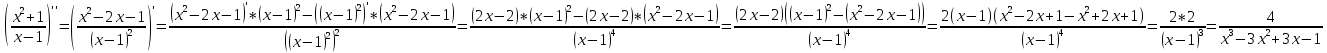
Находим первую производную от сложной функции.
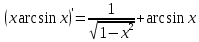
Находим вторую производную.
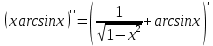
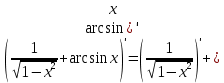
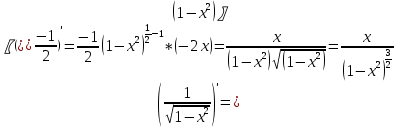
Согласно таблице производных:
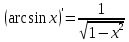
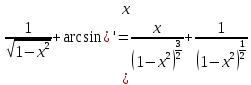
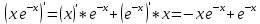
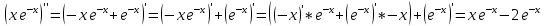
Ответ:
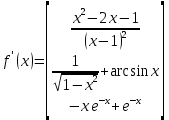
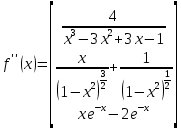
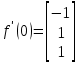
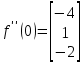
Задание 4. Докажите, что функция
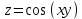удовлетворяет уравнению 
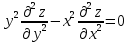.Находим первые производные по x и y
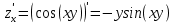
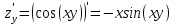
Находим вторые производные по x и y
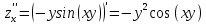
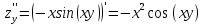
Подставим в исходное уравнение
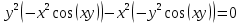
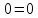
Задание 5. Дана функция
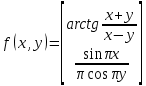. Найдите 
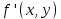. Вычислите 
.
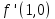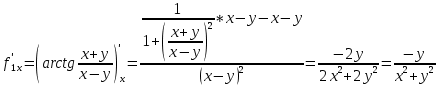
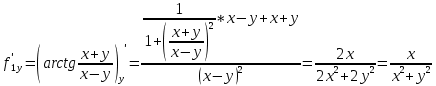
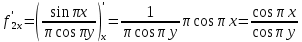
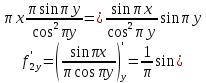
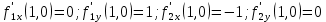
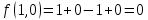
Ответ: 0
Задание 6. Дана функция
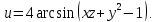Найдите:а) координаты вектора grad u в точке
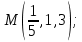
б)
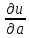в точке M в направлении вектора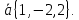 
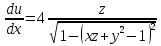
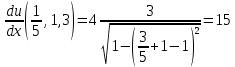
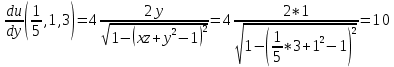
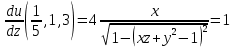
Ответ:
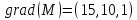
Задание 7. Найдите
, если 
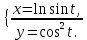Вычислите 
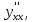если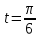 
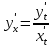
Первая производная
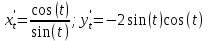
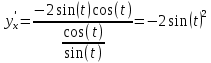
Вторая производная
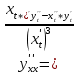
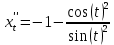
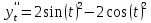
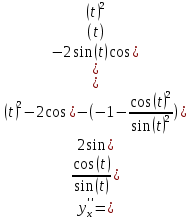
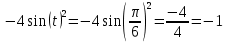
Ответ: -1
Задание 8. Функция
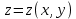задана неявно уравнением 
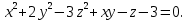Вычислите:а)
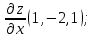
б)
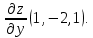
а)
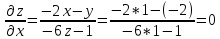
б)
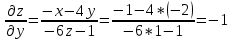
Задание 9. К графику функции
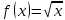в точке с абсциссой 
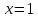проведена касательная. Найдите ординату точки графика касательной, абсцисса которой равна 31.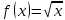 
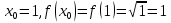
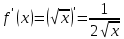
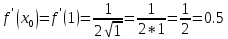
Уравнение касательной:
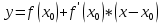
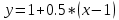
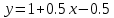
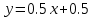
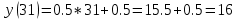
Ответ:
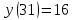
Задание 10. Найдите
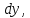если 
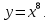Вычислите 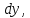если 
