Файл: Задача Методом изоклин построить интегральные кривые уравнения.docx
Добавлен: 08.11.2023
Просмотров: 24
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задача 1. Методом изоклин построить интегральные кривые уравнения
1.1.
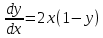.Решение:
Найдем уравнение изоклин. По определению уравнение имеет вид f(x,y)=k, где k=const. Следовательно, т.к.
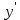=f(x,y)=2x(1-y), то k=2x(1-y) 
,
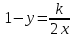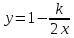Это уравнения изоклин.Задавая различные значения параметра k, можно получить семейство кривых, каждая из которых является изоклиной при определённом значении параметра k.
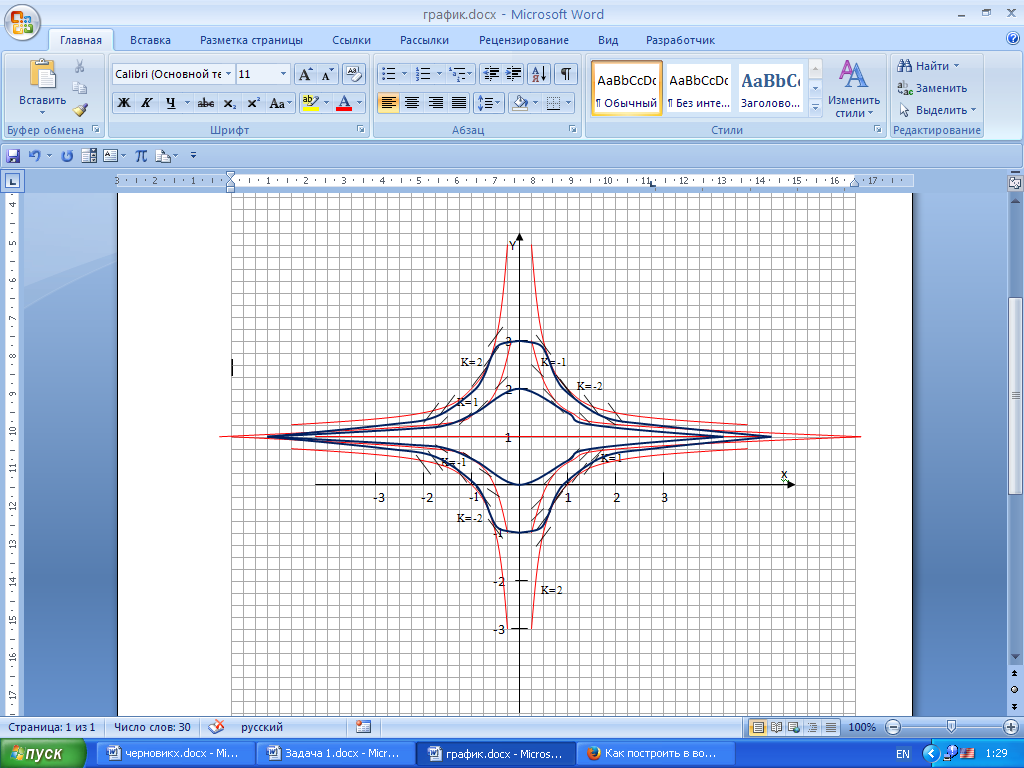
При k=0 получаем уравнение прямой y=1, и tgα=0 α=00 .
При k≠0 получаем семейство гипербол с центром в точке (0,1). При x→±∞; y→1, при x→0; y→±∞
Если k=1
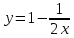, и tgα=1 α=450 , При k=-1
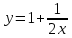, и tgα=-1 α=1350 , Если k=2
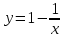, и tgα=2 α=630 , При k=-2
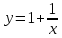, и tgα=-2 α=1170 , Построим график. Изоклины: гиперболы для k=±1 и k=±2.(Красным цветом) Интегральные кривые – синим цветом.
Задача 2. Решить уравнение допускающее понижение порядка
2.1.
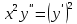
Решение: Это дифференциальное уравнение 2-го порядка. Оно позволяет снизить его порядок путем подстановки y′(x)=z(x) т.к. не содержит функцию у. Вторая производная y″=z′. Подставляя это значение в исходное уравнение получим: x2z′=z2, здесь
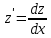. Это уравнение с разделяющимися переменными.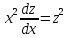
Разделим переменные:
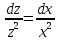
Проинтегрируем обе части этого равенства:
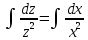или 
,
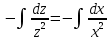
Получаем
; 
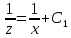
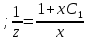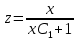
Вернемся к переменной y. Так как
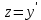, то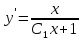 
;
; 
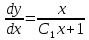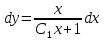
Переменные вновь разделены. Проинтегрируем обе части равенства.
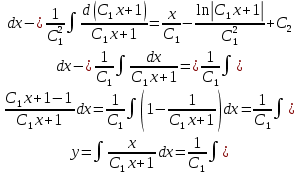
Таким образом - общее решение заданного уравнения
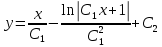
Ответ:
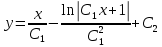
Задача 3.
Решить систему уравнений
3.1.
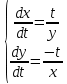
Решение:
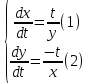;Из (1) уравнения выразим t:
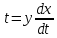
Подставим это выражение в уравнение (2)
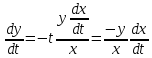; тогда 
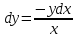. Это уравнение с разделяющимися переменными. Разделим переменные: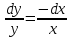
Проинтегрируем обе части:
; 
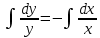
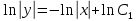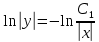
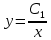
Подставляем полученное значение в (1) уравнение:
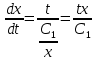
Снова разделяем переменные и интегрируем обе части:
;
;
;
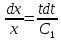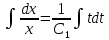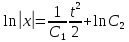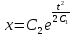
Тогда для функции y:
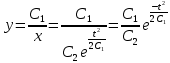
Ответ: общее решение системы:
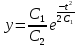
Задача 4. Вероятность появления события в каждом испытании равна 0,7. Сколько нужно провести испытаний, чтобы наивероятнейшее число появлений события равнялось 10?
Решение: Наивероятнейшее число появлений события определяется двойным неравенством:
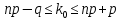
По условию нашей задачи:
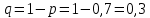
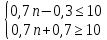
Из первого неравенства:
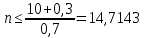
Из второго неравенства
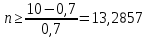
13,2857≤ n ≤14,7143
Так как n-целое число, получаем n=14.
Ответ: Необходимо провести 14 испытаний.