При построении полученных законов изменений токов и напряжения необходимо учесть длительность переходного процесса. Известно, что экспоненциальные функции за время 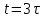изменяются на 95 % от своего максимального значения. Тогда можно принять, что переходный процесс в цепях первого порядка заканчивается через 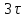с погрешностью 5%. Учитывая (1.11), определим время переходного процесса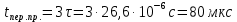Рассчитаем значения токов 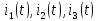и напряжения в различные моменты времени (таблица 1.3) и по результатам расчетов построим графики (рис. 1.6)Таблица 1.3

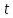	0	0,5		1,5	2	3	4
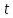, мкс	0	13,33	26,67	40	53,33	80	106,7
, мА	1,25	1,417	1,517	1,577	1,614	1,649	1,662
, мА	-1,25	-0,76	-0,46	-0,278	-0,169	-0,062	-0,023
, мА	2,5	2,175	1,976	1,856	1,783	1,712	1,685
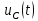, В	5	4,343	3,944	3,703	3,556	3,413	3,361

---

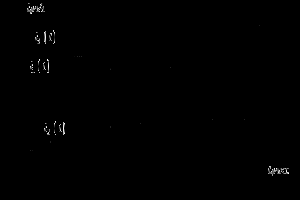
Рисунок 1.6 – Графики зависимостей

6. 
   Расчет тока операторным методом
   

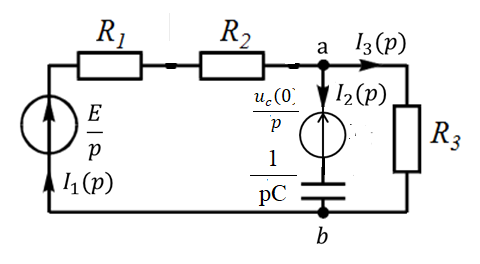
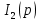
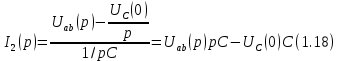
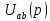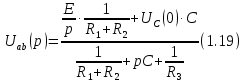
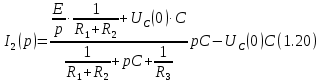
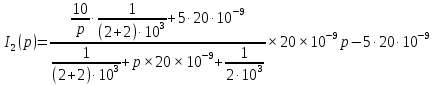
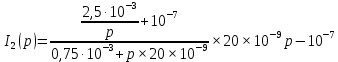
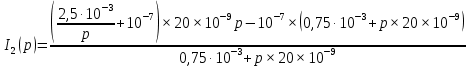
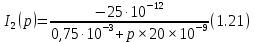
Для цепи при составляется операторная схема замещения (рис.1.7), Рисунок 1.7 – Операторная схема замещенияИспользуя закон Ома в операторной форме запишем выражение для изображения тока где может быть найдено по методу узловых напряжений:Подставляя (1.19) в (1.18) получимПосле числовых подстановок получаем изображение второго токаВ выражении 1.21 числитель обозначим за 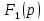, знаменатель обозначим как 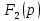, т.е.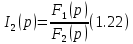Согласно теореме разложения, оригинал функции определяется 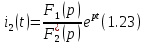В выражении р– корень функции 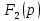. 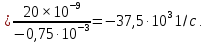В нашем случае pТогда, после числовых подстановок получаем оригинал тока , которое совпадает с выражением (1.15), полученным классическим методом.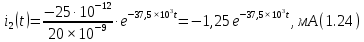

Задача 2

---

Задача посвящена временному и частотному (спектральному) методам расчета реакции цепей на сигналы произвольной формы. В качестве такого сигнала используется импульс прямоугольной формы. Электрические схемы цепей содержат емкости С или индуктивности L, а также сопротивления R. Для всех вариантов R₂=3 R₁._{В схемах, где имеется сопротивление} R₃ , его величина R₃  0,2R₁ . Во всех схемах входным напряжением u₁tявляется прямоугольный импульс длительностью t_и и амплитудой U_1.

1. 
   Перерисуйте схему Вашего варианта (см. табл. 1 и табл. 5). Выпишите исходные данные Вашего варианта (таблица 2.1).
   

Таблица 2.1

Варианты (две последние цифры пароля)	С, пФ или L, мкГн	R1 , кОм	tи , нс	U1 , В
От 00 до 09	20	1	30	3

Рисунок 2.1 – Исходная схема

Временной метод расчета

2. 
   Рассчитайте переходную g₂(t) и импульсную h₂(t) характеристики цепи по напряжению классическим или операторным методами (по выбору).
   
3. 
   Рассчитайте реакцию цепи в виде выходного напряжения, используя:
   

- интеграл Дюамеля;- интеграл наложения4. Постройте временные диаграммы входного и выходного напряжений в одинаковом масштабеЧастотный метод расчета5. Рассчитайте комплексные спектральные плотности входного 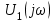и выходного 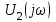сигналов.6. Рассчитайте и постройте графики модулей 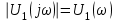, 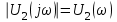и модуля комплексной передаточной функции цепи 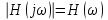, как функций от циклической частоты f в диапазоне частот 0 – 3/t_u.Решение:

---

2. 
   Рассчитайте переходную g₂(t) и импульсную h₂(t) характеристики цепи по напряжению классическим или операторным методами (по выбору).
   

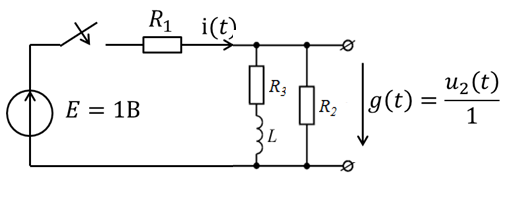
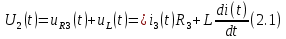
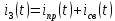
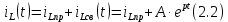
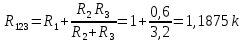
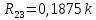
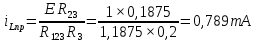
Рисунок 2.2 — Схема для определения переходной характеристикиR1 = 1k; R2 = 3k; R3 = 0,2k2.1 Переходная характеристика по напряжению определяется относительно выходного контура R₂C, поэтому можно записать, что:Закон изменения напряжения на емкости может быть определен с помощью формулы (1.9) расчета переходных процессов в схемах первого порядкагде 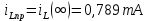;Постоянная интегрирования находится из условия нулевого начального условия ( 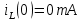):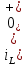Откуда 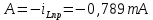.Корень характеристического уравнения определим из операторного сопротивления схемы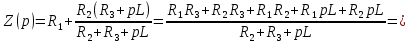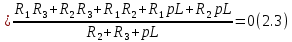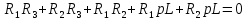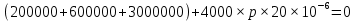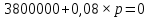Решение уравнения дает корень, 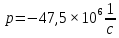Тогда ток в индуктивности 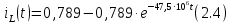Окончательно, переходная характеристика имеет вид

---

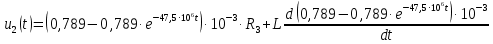
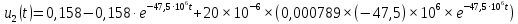
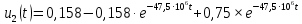
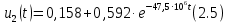
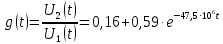
2.2 Импульсная характеристика цепиИмпульсная характеристика цепи определяется как производная от переходной характеристики цепи 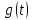. 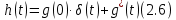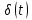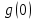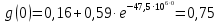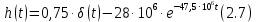Однако следует учесть, что если переходная характеристика отлична от нуля при t = 0, то есть имеет скачок при t = 0, то при дифференцировании появляется дополнительное слагаемое:где – импульсная функция (функция Дирака).Определим значение , подставив в выражение (2.5) t = 0Тогда импульсная характеристика цепи будет иметь вид2.3 Комплексная передаточная функция цепиКомплексная передаточная функция цепи H(jω) находится как отношение комплексного значения гармонического напряжения 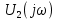к комплексному значению гармонического напряжения на входе цепи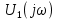 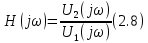Для схемы, приведенной на рис. 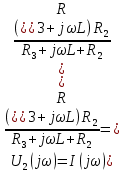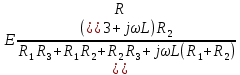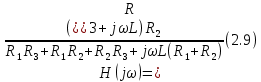2.1 легко получить:Тогда Анализ выражения (2.9) позволяет сделать вывод о том, что комплексная передаточная функция цепи по напряжению определяется только элементами цепи.

2. 
   Расчет выходного напряжения временным методом:
   
   1. 
      Интеграл Дюамеля
      

Для интервала времени

---

Смотрите также файлы

• Конспект развлечения ко Дню защиты детей во второй младшей группе "Счастье, солнце, дружба вот что детям нужно!".docx

• Воспитание нравственности и патриотизма у молодежи с помощью сферы физической культуры и спорта.docx

• Сотни тысяч разноцветных точек, которые пронизывают пространство системы, передавая информацию, важную и сверх важную, интересную и чрезвычайно захватывающую, а, возможно, теплое приветствие по случаю дня рождения.doc

• Административноправовое регулирование формирования кадрового резерва на федеральной государственной гражданской службе.docx

• 1. Схема процесса. Исходные данные.docx