Файл: Контрольная работа по дисциплине Теория электрических цепей Группа.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 08.11.2023

Просмотров: 61

Скачиваний: 3

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.




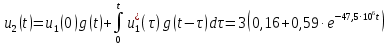
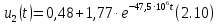
Для интервала времени











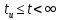
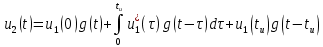
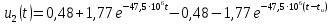
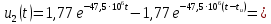
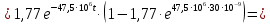
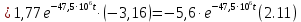
Окончательно, аналитическое выражение выходного напряжения цепи можно записать



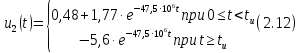
    1. Интеграл наложения

Интеграл наложения имеет вид:



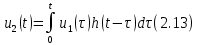
С учетом (2.7) реакция (2.13) заданной цепи на прямоугольный импульс будет равна:

Для интервала времени



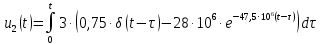
Используя фильтрующее свойство импульсной функции , получим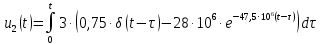







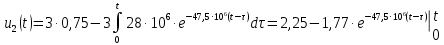
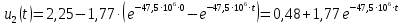
Для интервала времени










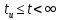
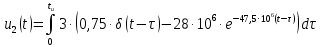
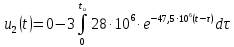
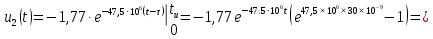
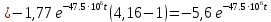
В результате получено аналитическое выражение напряжения на выходе цепи



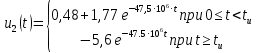
Сравнение результатов расчетов с (2.12) показывает, что они совпадают между собой.

4. Построение временных диаграмм

Диаграмма выходного напряжения строится с использованием выражения (2.12) путем подстановки в них соответствующих моментов времени.


Для проведения расчетов определим постоянную времени 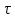. Согласно полученному выражению переходной характеристики цепи (2.4)



Результаты расчетов сведем в таблицу 2.2 и построим временные диаграммы напряжений на входе и выходе цепи (рис. 2.3).

Таблица 2.2

t
0
0,3

0,6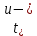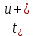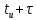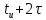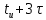











t, нс
0
9
18
30
30
51
72
93

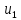, В
3
3
3
3
0
0
0
0

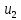, В
2,25
1,63
1,23
0,926
-1,347
-0,495
-0,182
-0,067

















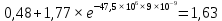
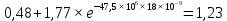
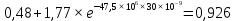
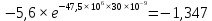
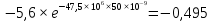
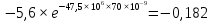
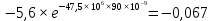
Рисунок 2.3 ­ Временные диаграммы входного и выходного напряжений

5. Расчет комплексной спектральной плотности входногоU1(jω) и выходного U2(jω) сигналов



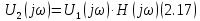
где 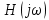– комплексная передаточная функция цепи по напряжению

модуль спектральной плотности входного напряжения:



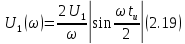
Амплитудно-частотная характеристика цепи (модуль комплексной передаточной функции)

R1 = 1k; R2 = 3k; R3 = 0,2k





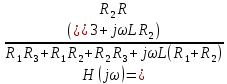
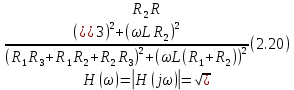
Модуль спектральной плотности выходного напряжения







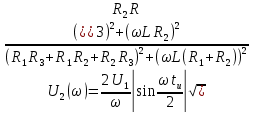
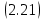
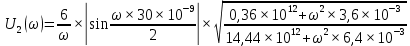
6. Рассчитаем графики модуле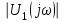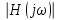й , и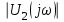

Для построения графиков полученных функций необходимо выбрать расчетные точки по частоте, при этом необходимо помнить, что спектральная плотность одиночного прямоугольного импульса обращается в ноль при частотах 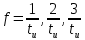и т.д. Поэтому дополнительно выберем промежуточные точки между этими частотами. Согласно заданию, максимальная частота соответствует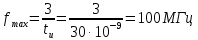



Результаты расчетов по (2.19), (2.20) и (2.21) сведем в таблицу 2.3.

Таблица 2.3












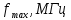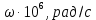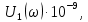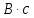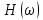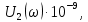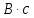0
0
90
0,158
14,21

2
12,56
89,47
0,245
21,93

4
25,13
87,89
0,377
33,17

8,3
52,15
81,11
0,564
45,78

10
62,8
77,27
0,606
46,8

33,3
209,44
0
0,732
0

50
314,2
19,11
0,742
14,18

66,7
418,9
0
0,745
0

70
439,6
4,174
0,746
3,113

100
628,4
0
0,748
0

По данным таблицы 2.3 построим графики (рис. 2.4, 2.5 и 2.6)









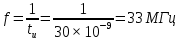
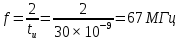
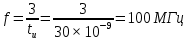
Рисунок 2.4 – Модуль спектральной плотности входного напряжения



Рисунок 2.5 – Амплитудно-частотная характеристика цепи



Рисунок 2.6 – Модуль спектральной плотности выходного напряжения

Смотрите также файлы