ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 33
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1
1)

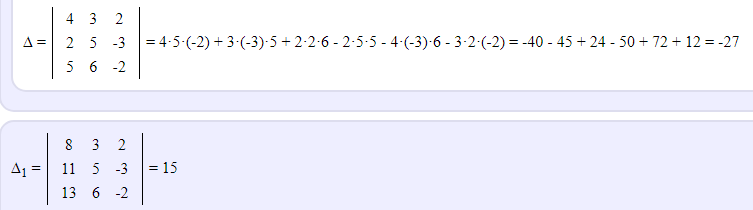
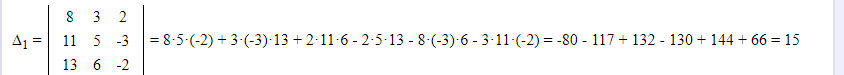

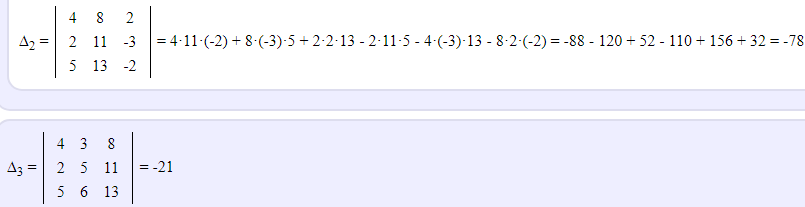
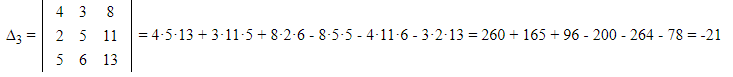
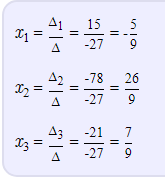
2)




3)
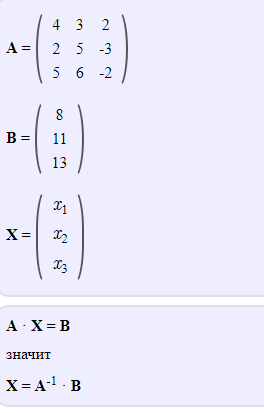

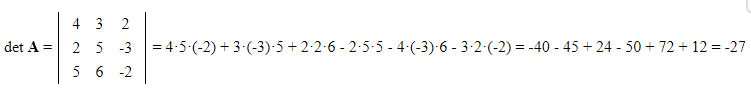









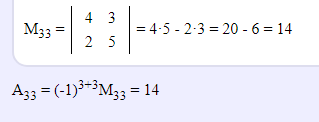


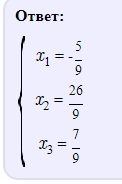
11
a) Упростим дробное выражение, умножив и числитель, и знаменатель на сопряженное знаменателя:
где
b) В итоге:
В итоге получаем:
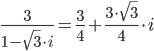
Ответ:
Представим как:
Для упрощения вычислений найдем все характеристики для
1. Находим тригонометрическую форму комплексного числа
.
Действительная часть числа x.
x=Re(z)=1
Мнимая часть числа y.
y=Im(z)=
Модуль комплексного числа |z|.
С учетом 3/4 получаем:
|z|
=
Поскольку x > 0, y > 0, то arg(z) находим как:
arg(z)=φ=
φ=
Таким образом, тригонометрическая форма комплексного числа:
21
31
41
51
[1;4]
Находим первую производную функции:
Приравниваем ее к нулю:
x1=2
Вычисляем значения функции на концах интервала
f(2)=-4
f(1)=1
f(4)=4
Ответ:
fmin = -4, fmax = 4
61
1) Область определения функции. Точки разрыва функции.
2) Четность или нечетность функции.
y(-x) = -y(x), нечетная функция
3) Периодичность функции.
4) Точки пересечения кривой с осями координат
.
Пересечение с осью 0Y
x=0, y=0
Пересечение с осью 0X
y=0
x1=0
5) Исследование на экстремум.
Поскольку f(-x)=-f(x), то функция является нечетной.
1. Находим интервалы возрастания и убывания. Первая производная.
или
Находим нули функции. Для этого приравниваем производную к нулю
4-2·x2=0
Откуда:
| | | |
| f'(x) < 0 | f'(x) > 0 | f'(x) < 0 |
| функция убывает | функция возрастает | функция убывает |
В окрестности точки x = -sqrt(2) производная функции меняет знак с (-) на (+). Следовательно, точка x = -sqrt(2) - точка минимума. В окрестности точки x = sqrt(2) производная функции меняет знак с (+) на (-). Следовательно, точка x = sqrt(2) - точка максимума.
2. Найдем интервалы выпуклости и вогнутости функции. Вторая производная.
или
Находим корни уравнения. Для этого полученную функцию приравняем к нулю.
Откуда точки перегиба:
x1=0
x2=
x3=
| | | | |
| f''(x) < 0 | f''(x) > 0 | f''(x) < 0 | f''(x) > 0 |
| функция выпукла | функция вогнута | функция выпукла | функция вогнута |
6) Асимптоты кривой.
Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты:
limx→∞k·x+b-f(x)
Находим коэффициент k:
Находим коэффициент b:
b=limx→∞f(x)-k·x
Получаем уравнение горизонтальной асимптоты:
y=0
Найдем наклонную асимптоту при x → -∞:
limx→-∞k·x+b-f(x)
Находим коэффициент k: