Файл: В итоге получаем.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 08.11.2023

Просмотров: 35

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


Находим коэффициент b:

b=limx→-∞f(x)-k·x

Получаем уравнение горизонтальной асимптоты:

y=0

71
81
91




















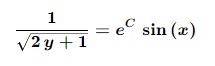
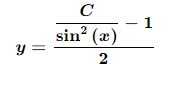
101


Проверим необходимое условие сходимости ряда (равенства предела 0):

Предел не равен 0, поэтому ряд расходится.
Следовательно, ряд: расходится.

111

Событие А: при пяти выстрелах произошло ровно 2 попадания. Вероятность попадания при одном выстреле: 0.8. Вероятность промаха при одном выстреле: 1 - 0.8 = 0.2. Результатом будет пересечение различных вариантов объединений событий, соответствующих двум попаданиям и трем промахам. Т. е. первый и второй - попал, третий, четвертый пятый - нет, или первый третий попал, остальные - нет, или первый четвертый.. . и т. д. Вариантов двух попаданий при пяти выстрелах С (2,5) = 10. Р (А) = (0.8)^2 * (0.2)^3 * 10 = 0.0512

121

1.1) В результате эксперимента получены данные, записанные в виде статистического ряда. Требуется:

а) записать значения результатов эксперимента в виде вариационного ряда;

б) найти размах варьирования и разбить его на 9 интервалов;

в) построить полигон частот, гистограмму относительных частот и график эмпирической функции распределения;

г) Найти числовые характеристики выборк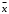и и ;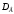

д) принять в качестве нулевой гипотезу Н0: генеральная совокупность, из которой извлечена выборка, имеет нормальное распределение, проверить её, пользуясь критерием Пирсона при уровне значимости ;

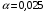е) найти доверительные интервалы для математического ожидания и среднего квадратичного отклонения при степени надёжности .

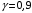17,1
21,4
15,9
19,1
22,4
20,7
17,9
18,6
21,8
16,1

19,1
20,5
14,2
16,9
17,8
18,1
19,1
15,8
18,8
17,2

16,2
17,3
22,5
19,9
21,1
15,1
17,7
19,8
14,9
20,5

17,5
19,2
18,5
15,7
14,0
18,6
21,2
16,8
19,3
17,8

18,8
14,3
17,1
19,5
16,3
20,3
17,9
23,0
17,2
15,2

15,6
17,4
21,3
22,1
20,1
14,5
19,3
18,4
16,7
18,2

16,4
18,7
14,3
18,2
19,1
15,3
21,5
17,2
22,6
20,4

22,8
17,5
20,2
15,5
21,6
18,1
20,5
14,0
18,9
16,5

20,8
16,6
18,3
21,7
17,4
23,0
21,1
19,8
15,4
18,1

18,9
14,7
19,5
20,9
15,8
20,2
21,8
18,2
21,2
20,1


РЕШЕНИЕ

а) Записываем вариационный ряд. Располагаем значения результатов эксперимента в порядке возрастания.


14,0
14,0
14,2
14,3
14,3
14,5
14,7
14,9
15,1
15,2

15,3
15,4
15,5
15,6
15,7
15,8
15,8
15,9
16,1
16,2

16,3
16,4
16,5
16,6
16,7
16,8
16,9
17,1
17,1
17,2

17,2
17,2
17,3
17,4
17,4
17,5
17,5
17,7
17,8
17,8

17,9
17,9
18,1
18,1
18,1
18,2
18,2
18,2
18,3
18,4

18,5
18,6
18,6
18,7
18,8
18,8
18,9
18,9
19,1
19,1

19,1
19,1
19,2
19,3
19,3
19,5
19,5
19,8
19,8
19,9

20,1
20,1
20,2
20,2
20,3
20,4
20,5
20,5
20,5
20,7

20,8
20,9
21,1
21,1
21,2
21,2
21,3
21,4
21,5
21,6

21,7
21,8
21,8
22,1
22,4
22,5
22,6
22,8
23,0
23,0

б) Находим размах варьирования .

.

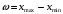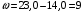По формул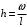е , где 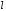- число интервалов, вычисляем длину частичного интервала: .

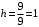В качестве границы первого интервала возьмём 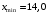. Границы следующих интервалов вычисляем по формул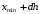е: , где .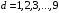

Находим середины интервалов: 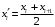. Подсчитываем число значений результатов эксперимента, попавших в каждый интервал, т.е. находим частоты интервалов 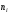. Далее вычисляем относительные частоты 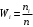, ( 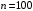) и их плотности 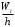. Все полученные результаты помещаем в таблицу.


Номер частичного интервала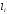

Границы интервала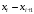

Середина интервала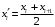

Частота интервала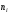

Относительная частота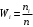

Плотность относительной частоты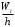

1

2

3

4

5

6

7

8

9
14,0-15,0

15,0-16,0

16,0-17,0

17,0-18,0

18,0-19,0

19,0-20,0

20,0-21,0

21,0-22,0

22,0-23,0
14,5

15,5

16,5

17,5

18,5

19,5

20,5

21,5

22,5
8

10

9

15

16

12

12

11

7
0,08

0,1

0,09

0,15

0,16

0,12

0,12

0,11

0,07
0,08

0,1

0,09

0,15

0,16

0,12

0,12

0,11

0,07



-
-
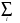100
1
1


в) Строим полигон частот и гистограмму относительных частот.






15



10

5




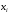
14,5 15,5 16,5 17,5 18,5 19,5 20,5 21,5 22,5

Смотрите также файлы