0,2


0,15




0,1



0,05




14 15 16 17 18 19 20 21 22 23

Находим значения эмпирической функции распределения

---

.



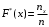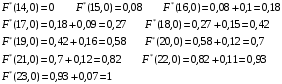
Строим график эмпирической функции распределения:



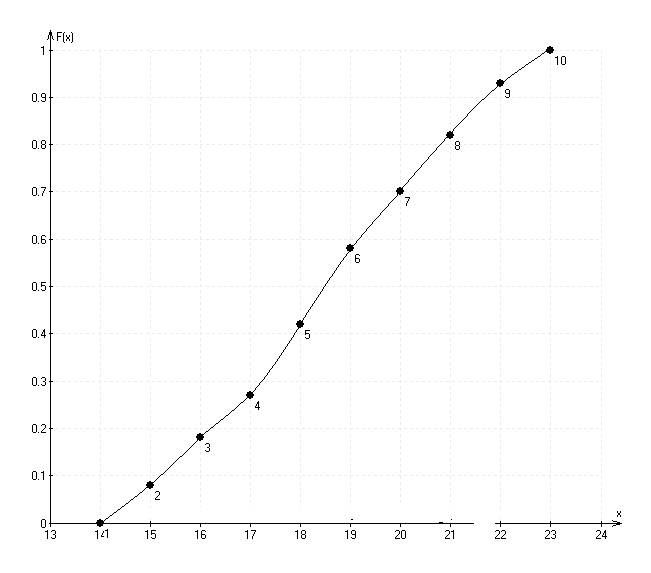
г) Найдём выборочное среднее 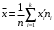и выборочную дисперсию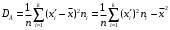

Составляем расчётную таблицу:

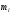	Границы интервала	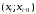Середина интервала	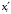Частота интервала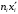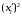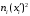
1 2 3 4 5 6 7 8 9	14,0-15,0 15,0-16,0 16,0-17,0 17,0-18,0 18,0-19,0 19,0-20,0 20,0-21,0 21,0-22,0 22,0-23,0	14,5 15,5 16,5 17,5 18,5 19,5 20,5 21,5 22,5	8 10 9 15 16 12 12 11 7	116 155 148,5 262,5 296 234 246 236,5 157,5	210,25 240,25 272,25 306,25 342,25 380,25 4202,25 462,25 506,25	1682 2402,5 2450,25 4593,75 5476 4563 5043 5084,75 3543,75
	-	-	100	1852		34839

Находим выборочное среднее:



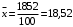
Находим выборочную дисперсию:



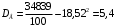
Находим выборочное среднее квадратическое отклонение:



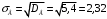
Выборочная дисперсия является смещённой оценкой генеральной дисперсии, а исправленная дисперсия – несмещённой оценкой:

---

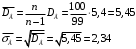
д) Согласно критерию Пирсона необходимо сравнить эмпирические и теоретические частоты. Эмпирические частоты даны. Найдём теоретические частоты. Для этого пронумеруем Х, т.е. перейдём к случайной величине 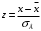и вычислим концы интервалов: 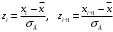, причём наименьшее значение , точнее 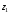положим стремящимся к 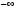, а наибольшее, точнее 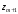- стремящемся к .

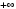Строим расчётную таблицу:

	Границы интервала ( 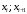)			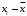	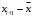Границы интервала ( )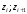
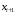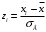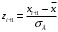1 2 3 4 5 6 7 8 9	14 15 16 17 18 19 20 21 22	15 16 17 18 19 20 21 22 23	- -3,52 -2,52 -1,52 -0,52 0,48 1,48 2,48 3,48	-3,52 -2,52 -1,52 -0,52 0,48 1,48 2,48 3,48 -	- -1,52 -1,09 -0,66 -0,22 0,21 0,64 1,07 1,5	-1,52 -1,09 -0,66 -0,22 0,21 0,64 1,07 1,5 -

Находим теоретические вероятности 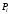и теоретические частоты: .

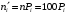Значения

---

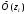
и 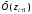находим по таблице Лапласа.

Составляем расчётную таблицу.

	Границы интервала ( )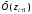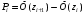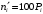
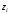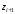1 2 3 4 5 6 7 8 9	- -1,52 -1,09 -0,66 -0,22 0,21 0,64 1,07 1,5	-1,52 -1,09 -0,66 -0,22 0,21 0,64 1,07 1,5 -	-0,5000 -0,4357 -0,3621 -0,2454 -0,0871 0,0832 0,2389 0,3577 0,4332	-0,4357 -0,3621 -0,2454 -0,0871 0,0832 0,2389 0,3577 0,4332 0,5000	0,0643 0,0736 0,1167 0,1583 0,1703 0,1557 0,1188 0,0755 0,0668	6,43 7,36 11,67 15,83 17,03 15,57 11,88 7,55 6,68
	-	-	-	-	1	100

Вычислим наблюдаемое значение критерия Пирсона.

Для этого составляем расчётную таблицу.

Последние два столбца служат для контроля вычислений по формуле:

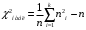
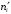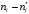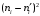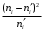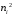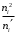1 2 3 4 5 6 7 8 9	8 10 9 15 16 12 12 11 7	6,43 7,36 11,67 15,83 17,03 15,57 11,88 7,55 6,68	1,57 2,64 -2,67 -0,83 -1,03 -3,57 0,12 3,45 0,32	2,4649 6,9696 7,1289 0,6889 1,0609 12,7449 0,0144 11,9025 0,1024	0,3831 0,9467 0,6107 0,0431 0,0619 0,8176 0,0012 1,5791 0,0150	64 100 81 225 256 144 144 121 49	9,9533 13,5869 6,9409 14,2135 15,0323 9,2485 12,1212 16,0265 7,3353
	100	100	-	-	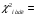4,4584	-	104,4584

---

Контроль:



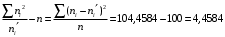
По таблице критических точек распределения 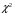, уровню значимости и числу степеней свободы 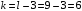( - число интервалов) находим: .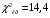

Так как 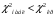, то гипотеза Н₀ о нормальном распределении генеральной совокупности принимается.

е) Найдем доверительный интервал для математического ожидания для нормального распределения и неизвестной дисперсии. Воспользуемся формулой: ,

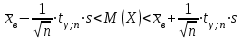где 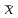= 18,52, n = 100, s= 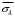= 2,34.

Значение t(;k) найдем по таблицам tраспределения Стьюдента.

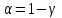= 1 – 0,9 = 0,1 и k = 100 – 1 = 99.

Получим: 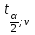= t_0,05;99 = 1,984. 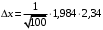 0,46.

Получим: 18,52 – 0,46 < M(x) < 18,52 + 0,46 или 18,06 < M(x) < 18,98.

Построим доверительный интервал для среднего квадратического отклонения. Применим формулу: 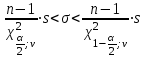, где  = n – 1 = 100 – 1 = 99.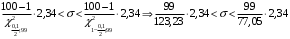



Получим: 1,88    3,01.

---

Смотрите также файлы

• 3. Расчётноконструктивный раздел 1 Определение нормативных и расчетных величин нагрузок на каркас здания, создание расчетных сочетаний нагрузок.docx

• Утверждаю начальник 50 псч 1 псо фпс гпс гу мчс россии по Ростовской области М. С. Диденко 20 года методический план.doc

• Тест тгп.docx

• Финансовые рынки, институты и инструменты.ppt

• 3 билет (совпал,2022) 1) артерия эластического типа (аорта) 2) яичник млекопитающего 4.pdf