Файл: Имеются следующие данные за год по заводам одной по заводам одной промышленной компании.docx
Добавлен: 08.11.2023
Просмотров: 592
Скачиваний: 15
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Частное профессиональное образовательное учреждение «ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ КОЛЛЕДЖ» |
Практическое задание
| по | статистика |
дисциплине
| Выполнил(а) студент(ка) | | |||
| | фамилия имя отчество | |||
| Идентификационный номер: | | |||
| | | |||
| | | |||
| | | |||
| | | |||
| | | |||
| | | |||
Пермь 2023
Задача 1. Имеются следующие данные за год по заводам одной по заводам одной промышленной компании.
| Завод | Среднее число рабочих, чел. | Основные фонды, млн. руб. | Продукция, млн. руб. | Завод | Среднее число рабочих, чел. | Основные фонды, млн. руб. | Продукция, млн. руб. | |||||
| 1 | 700 | 250 | 300 | 9 | 1 400 | 1 000 | 1 600 | |||||
| 2 | 800 | 300 | 360 | 10 | 1 490 | 1 250 | 1 800 | |||||
| 3 | 750 | 280 | 320 | 11 | 1 600 | 1 600 | 2 250 | |||||
| 4 | 900 | 400 | 600 | 12 | 1 550 | 1 500 | 2 100 | |||||
| 5 | 980 | 500 | 800 | 13 | 1 800 | 1 900 | 2 700 | |||||
| 6 | 1 200 | 750 | 1 250 | 14 | 1 700 | 1 750 | 2 500 | |||||
| 7 | 1 100 | 700 | 1 000 | 15 | 1 900 | 2 100 | 3 000 | |||||
| 8 | 1 300 | 900 | 1 500 | | | | | | | | | |
На основании приведенных данных составьте групповую таблицу зависимости выработки на одного рабочего от величины заводов по числу рабочих. Число групп – три.
РЕШЕНИЕ ЗАДАЧИ 1.
Определим выработку:
Величину интервала рассчитаем по формуле:
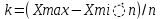 , где хmax, xmin – максимальное и минимальное значения объема продукции, а n – количество групп.
, где хmax, xmin – максимальное и минимальное значения объема продукции, а n – количество групп.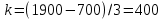
Определим границы 3-х групп:
-
700-1100 -
1100-1500 -
1500-1900
Рассчитаем показатели по каждой группе. Сначало вычислим выработку на одного рабочего количество произведенной продукции по формуле:
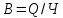 , где В-выработка продукции, количество произведенной продукции в натуральных или стоимостных показателях, Ч-численность работников.
, где В-выработка продукции, количество произведенной продукции в натуральных или стоимостных показателях, Ч-численность работников. Группа 1 700-1100
| Завод | Среднее число рабочих, чел. | Основные фонды, млн руб. | Продукция, млн руб. | Выработка продукции на одного работника |
| 1 | 700 | 250 | 300 | 0.428 |
| 2 | 800 | 300 | 360 | 0.45 |
| 3 | 750 | 280 | 320 | 0.426 |
| 4 | 900 | 400 | 600 | 0.666 |
| 5 | 980 | 500 | 800 | 0.816 |
| 7 | 1 100 | 700 | 1 000 | 0.909 |
Итого: 6 5230 2430 3380 0.646
Группа 2 1100-1500
| Завод | Среднее число рабочих, чел. | Основные фонды, млн руб. | Продукция, млн руб. | Выработка продукции на одного работника |
| 6 | 1 200 | 750 | 1 250 | 1.041 |
| 8 | 1 300 | 900 | 1 500 | 1.153 |
| 9 | 1 400 | 1 000 | 1 600 | 1.142 |
| 10 | 1 490 | 1 250 | 1 800 | 1.208 |
Итого: 4 5390 3900 6150 1.141
Группа 3 1500-1900
| Завод | Среднее число рабочих, чел. | Основные фонды, млн руб. | Продукция, млн руб. | Выработка продукции на одного работника |
| 11 | 1 600 | 1 600 | 2 250 | 1.406 |
| 12 | 1 550 | 1 500 | 2 100 | 1.354 |
| 13 | 1 800 | 1 900 | 2 700 | 1.5 |
| 14 | 1 700 | 1 750 | 2 500 | 1.47 |
| 15 | 1 900 | 2 100 | 3 000 | 1.578 |
12550_1.467_Результаты_групп_в_таблице'>Итого: 5 8550 8850 12550 1.467
Результаты групп в таблице
| № | Величина интервала | Кол-во заводов | Число рабочих | Основные фонды в млн. руб. | Продукция в млн. руб. | Выработка продукции на одного работника |
| 1 | 700-1100 | 6 | 5230 | 2430 | 3380 | 0.646 |
| 2 | 1100-1500 | 4 | 5390 | 3900 | 6150 | 1.141 |
| 3 | 1500-1900 | 5 | 8550 | 8850 | 12550 | 1.467 |
Выводы: с увеличением количества рабочих увеличиваются основные фонды и выработка продукции на одного человека.
3адача 2. Выпуск продукции на заводе в 2020 г. составил 160 млн руб. По плану на 2021 г. предусматривалось выпустить продукции на 168 млн руб., фактически же выпуск составил 171,36 млн руб. Вычислите относительные величины планового задания и выполнения плана.
РЕШЕНИЕ ЗАДАЧИ 2
Вычислим относительные показатели по формулам:
ОВПЗ (относительная величина планового задания)
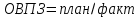 *100%=
*100%=168: 160 *100%=105%
ОВВП (относительная величина выполнения плана)
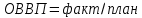 * 100% =
* 100% = 171.36:168*100%=102%
ВЫВОД: на 2021 год планировалось увеличить выпуск продукции по сравнению 2020 года на 5%, фактически план выпуска продукции был перевыполнен на 2%.
Задача 3. На основании данных, представленных в таблице, определите установленную среднюю продолжительность трудового дня производственного рабочего по заводу в целом:
| | | | | |
| Показатель | 1 цех | 2 цех | 3 цех | 4 цех |
| Количество смен | 3 | 3 | 2 | 1 |
| Число рабочих в смену | 600 | 800 | 400 | 200 |
| Продолжительность смены | 8 | 8 | 8 | 6 |
РЕШЕНИЕ ЗАДАЧИ
В первую очередь надо узнать сколько людей работает по цехам и заводу в целом.
1цех-3*600=1800
2 цех-3*800=2400
3 цех-2*400=800
4 цех-1*200=200 Итого на заводе работают 5200 человек, из них 5000 человек работают по 8 часов, что составляет 96.2% людей. По 6 часов работает 200 человек, что составляет 3.2% людей. Теперь узнаем среднюю продолжительность смены: 8*96.2%=6*3.2%=7,888
ВЫВОД: средняя продолжительность смены по заводу составляет 7,888 часов.
Задача 4. Имеются следующие данные о распределении рабочих цеха по размеру месячной заработной платы:
| Размер зарплаты, тыс. руб. | до 5,0 | 5,0-7,5 | 7,5-10,0 | 10,0-12,5 | свыше 12,5 |
| Число рабочих, чел. | 15 | 15 | 25 | 65 | 30 |
Определите среднюю месячную зарплату рабочих цеха, моду и медиану, среднеквадратическое отклонение икоэффициент вариации.
РЕШЕНИЕ ЗАДАЧИ
Определим среднюю месячную зарплату по формуле
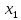 =2.5+5/2=3.75
=2.5+5/2=3.75 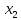 =5+7,5/2=6,25 х3=7,5+10/2=8,75
=5+7,5/2=6,25 х3=7,5+10/2=8,75 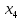 =10+12,5/2=11,25 х5=12,5+15/2=13,75
=10+12,5/2=11,25 х5=12,5+15/2=13,75х=3,75*15+6,25*15+8,75*25+11,25*65+13,75*30/150=1512,5/150=10,083
Средняя заработная плата составляет 10,083 тыс.руб. Этот ряд имеет равные интервалы, то мода находится в интервале наибольшей частотой, то есть в интервале 10,0 - 12,5 тыс. руб.
Следовательно, её можно вычислить по формуле:
Mb=xₙ+h*
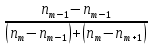
Нижняя граница модального интервала, величина модального интервала:
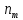 -частота модального периода,
-частота модального периода,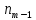 предмодального периода,
предмодального периода, 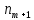 постмодального периода
постмодального периодаMb= 10,0+2,5*
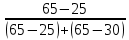 =11,33
=11,33Медиана определяется по формуле Ме= xₙ+h
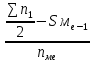 , нижняя граница медианного периода, величина медианного периода,
, нижняя граница медианного периода, величина медианного периода,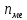 -частость медианного периода,
-частость медианного периода,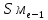 -накопленная частость предмедианного периода
-накопленная частость предмедианного периодаМе= 10,0+2.5
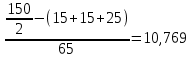 Ответ:медиана ровна 10,769
Ответ:медиана ровна 10,769 Дисперсию можно определить по формуле: