Ход урока

I. Устная работа.

1. Повторить правило сложения отрицательных чисел. Привести свои примеры.

2. Повторить правило сложения чисел с разными знаками. Привести свои примеры.

3. Решить устно № 1072 (з; и) и 1073 (а).

4. Решить № 1075 (б; в), записывая решение только на доске.

II. Тренировочные упражнения.

1. Решить № 1066 (н – р) на доске и в тетрадях с помощью учителя.

Решение.

н) ;

о) ;

п) ;

р) = 0.

2. Решить № 1067 (в; г) на доске и в тетрадях.

Решение.

в) (–10 + (–1,3)) + (5 + 8,7) = –11,3 + 13,7 = 13,7 – 11,3 = 2,4;

г) (11 + (–6,5)) + (–3,2 + (–6)) = 4,5 + (–9,2) = – (9,2 – 4,5) = –4,7.

3. Решить № 1070 (в; г).

Решение.

в)

;

г) .

4. Решить № 1068.

5. Повторение ранее изученного материала:

Решить задачу № 1078 (д – з) на доске и в тетрадях.

III. Самостоятельная работа.

Вариант I.

1. Выполните сложение:

а) –543 + 458; г) ;

б) 0,54 + (–0,83); д) .

в) ;

2. Выполните действия .

3. Найдите значение выражения х + 2,6, если х = –1,47;

; х = –18; .

4. Сколько решений имеет уравнение |х + 2| = –5?

Вариант II.

1. Выполните сложение:

а) 257 + (–314); б) –0,28 + (–0,18); в) –6 + ;

г) ; д)

---

.

2. Выполните действия .

3. Найдите значение выражения у + (–4,2), если у = 1,83;

у = ; у = 16; у = .

4. Сколько решений имеет уравнение |у – 9| = –6?

Домашнее задание: решить № 1081 (м – р), № 1082, № 1086.
Вычитание.

Урок 1

Цели: вспомнить, в чем смысл вычитания чисел; ввести понятие вычитания отрицательных чисел.

Ход урока

I. Анализ самостоятельной работы.

1. Сообщить результаты выполнения работы.

2. Решить на доске примеры, вызвавшие затруднения у учащихся.

II. Повторение ранее изученного материала.

1. Какие числа называются противоположными? Привести свои примеры.

2. Решить устно № 1100 и 1101 (а; б).

III. Объяснение нового материала.

1. Вычитание отрицательных чисел имеет тот же смысл, что и вычитание положительных чисел: по заданной сумме и одному из слагаемых находят другое слагаемое. Чтобы найти искомое слагаемое, можно прибавить к сумме число, противоположное известному слагаемому. Например, 8 + 3 = 11, и потому 11 – 8 = 3.

Но 11 + (–8) = 3.

2. Чтобы из данного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому:

а – в = а + (–в).

3. Любое выражение, содержащее лишь знаки сложения и вычитания, можно рассматривать как сумму.

например, –18 – 14 = –18 + (–14) = –32;

–8 + 6 – k = –8 + 6 + (–k) = –2 + (–k).

4. Если уменьшаемое и вычитаемое равны, то их разность равна нулю.

64 – 64 = 0; 2,8 – 2,8 = 2,8 + (–2,8) = 0.

IV. Закрепление изученного материала.

1. Решить № 1091 (а; ж; з) на доске и в тетрадях, 1091 (б; д; и) – самостоятельно с последующей проверкой.

2. Решить № 1093 на доске и в тетрадях.

Решение.

а) –28 – (–32) = –28 + 32 = 4;

б) –46 – 30 = –46 + (–30) = –76;

в) 50 – (–24) = 50 + 24 = 74;

г) х – 80 = х + (–80);

д) –30 – р = –30 + (–р);

е) 6 – (–а) = 6 + а.

3. Решить № 1090 (а; б; в) с комментированием на месте.

4. Решить № 1091 (в; г; е) самостоятельно.

Решение.

в) –21 – (–19) = –21 + 19 = –2;

г) 9 – (–9) = 9 + 9 = 18;

е) –5,6 – (–3,1) = –5,6 + 3,1 = –2,5.

5. Решить устно № 1087 по демонстрационному термометру.

Решение.

х + (–12) = –8; х = –8 – (–12) = –8 + 12 = 4.

---

Ответ: было утром 4 °С.

6. Решить задачу № 1107 (1) на повторение ранее изученного материала.

Решение.



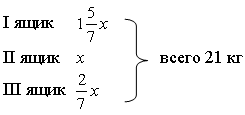
Составим и решим уравнение:



3х = 21

х = 21 : 3

х = 7.

Во втором ящике было 7 кг гвоздей, в третьем ящике было (кг) гвоздей, в первом ящике было 21 – (7 + 2) = 21 – 9 = 12 (кг).

Ответ: 12 кг; 7 кг; 2 кг.

V. Итог урока.

1. Что означает вычитание отрицательных чисел?

2. Каким действием можно заменить вычитание числа а из числа в?

3. Выполните вычитание:

а) 48 – (–15); б) 25 – 32; в) –5,5 – 2,8; г) 3,7 – 4,5; д) .

Домашнее задание: изучить п. 34 (1-я часть); решить № 1109 (а – е), № 1113 (а; б), № 1116.

Урок 2

Цели: упражнять учащихся в вычитании отрицательных чисел; научить находить длину отрезка на координатной прямой; развивать логическое мышление учащихся.

Ход урока

I. Устная работа.

1. Повторить правила сложения отрицательных чисел и сложения чисел с разными знаками. Привести примеры.

2. Решить устно № 1098 (а; б; г) и 1101 (в; г).

3. Решить № 1104, записывая на доске приведенные учащимися примеры.

4. Двое учащихся на доске выполняют упражнения из домашнего задания: 1) № 1109 (а – з); 2) № 1116.

Решение.

30 % = 0,3.

Пусть в альбоме было х российских марок, тогда иностранных марок в альбоме было 0,3х. Всего в альбоме 1105 марок.

х + 0,3х = 1105

1,3х = 1105

х = 1105 : 1,3 = 11050 : 13 = 850

х = 850.

В альбоме было 850 российских марок, а иностранных 1105 – 850 = 255 (марок).

Ответ: 255 марок, 850 марок.

II. Выполнение упражнений.

1. Решить № 1091 (к; л; р; н; п) самостоятельно с проверкой; 1091 (о; с; т) решить на доске и в тетрадях.

Решение.

к) –7,62 – (–7,62) = –7,62 +7,62 = 0;

л) –0,21 – 0 = –0,21 + 0 = –0,21;

р) ;

н) ;

п) ;

о)

---

;

с) ;

т)

.

2. Решить устно № 1094.

3. Решить № 1092 (а; в) на доске и в тетрадях, 1092 (б) – самостоятельно.

Решение.

а) –2 + х = 4,3 б) 8,1 + у = –6 в) 5 – х = 1,7

х = 4,3 – (–2) у = –6 – 8,1 х = 5 – 1,7

х = 4,3 + 2 у = –6 + (–8,1) х = 3,3.

х = 6,3. у = –14,1.

Ответ: х = 6,3. Ответ: у = –14,1. Ответ: х = 3,3.

4. Решить № 1088, используя демонстрационный термометр.

5. Решить № 1096 (а; в; д) на доске и в тетрадях, № 1096 (б; г; е) – самостоятельно.

а) (62 – 28) – 40 = 34 – 40 = 34 + (–40) = –6;

б) –50 + (37 + 30) = –50 + 67 = 17;

в) –6 – (–8 –20) = –6 – (–28) =–6 + 28 = 22;

г) –7 –(–12 + 13) = –7 –1 = –7 + (–1) = –8;

д) 4,1 – (–1,8 + 2,5) = 4,1 – 0,7 = 3,4;

е) (–3,2 + 60) – 0,8 = 56,8 – 0,8 = 56.

III. Изучение нового материала.

1. Разобрать решение задачи на с. 185 учебника.

2. Правило: Чтобы найти длину отрезка на координатной прямой, надо из координаты его правого конца вычесть координату его левого конца.

3. Решить задачу № 1097 (а; в; д).

а) 8 – 2 = 6; в) 6 – (-1) = 6 + 1 =7; д) 3,2 – (–4,7) = 3,2 + 4,7 = 7,9.

IV. Повторение ранее изученного материала.

1. Решить задачу № 1107 (2) самостоятельно.

2. Решить № 1103.

V. Итог урока.

1. Ответить на вопросы на с. 185 учебника.

2. Найти расстояние между точками:

а) А (–5,2) и В (–1,8);

б) С и Д .

3. Решить уравнение:

а) 2,4 + х = –2,8;

б) 18,24 – у = 20.

Домашнее задание: выучить правила п. 34; решить № 1109 (ж – к), 1111, 1113 (в; г), 1115.

Прочитать исторический материал на с. 190.
Урок 3

Цели: закрепить изученный материал, вырабатывать навыки сложения чисел; проверить степень усвоения учащимися материала; подготовиться к контрольной работе.

Ход урока

I. Устная работа.

1. Решить устно № 1098 (в; д; е) и 1104.

2. Решить уравнения № 1103 (д; е) на доске.

3. Двое учащихся работают у доски:

1) один ученик решает задачу № 1106;

2) второй ученик решает задачу № 1115.

II. Выполнение упражнений.

1. Решить № 1090 (г; д; е) устно.

2. Решить № 1095 с комментированием на месте.

3. Решить № 1092 (д; г; е) на доске и в тетрадях.

Решение.

---

г) д) е)





.

Ответ: .

Ответ: .

Ответ: .

4. Решить № 1089 (устно).

5. Решить задачу № 1097 (г; е) на доске и в тетрадях, № 1097 (б) – самостоятельно.

6. Решить № 1096 (ж; и) самостоятельно, № 1096 (к; л; м) – на доске и в тетрадях.

Решение.

ж) ;

и) ;

к) ;

л) ;

м)

.

III. Самостоятельная работа.

Вариант I.

---

Смотрите также файлы

• 1 Задание на расчетнографическую работу.docx

• Пн Геометрия 3тосан Бекітемін ыса мерзімді жоспар 1сабак.docx

• Аттестация тест лд2023.docx

• Развитие семьи и брака. Причины разводов. Введение.docx

• Исследование виртуальной позиционной сар уровня жидкости в резервуаре.docx