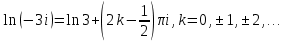Группа:

Вариант: 3

Задание 1. Однородная пластинка имеет форму четырёхугольника (см. рис.). Указаны координаты вершин. С помощью двойного интеграла вычислить координаты центра масс пластины.



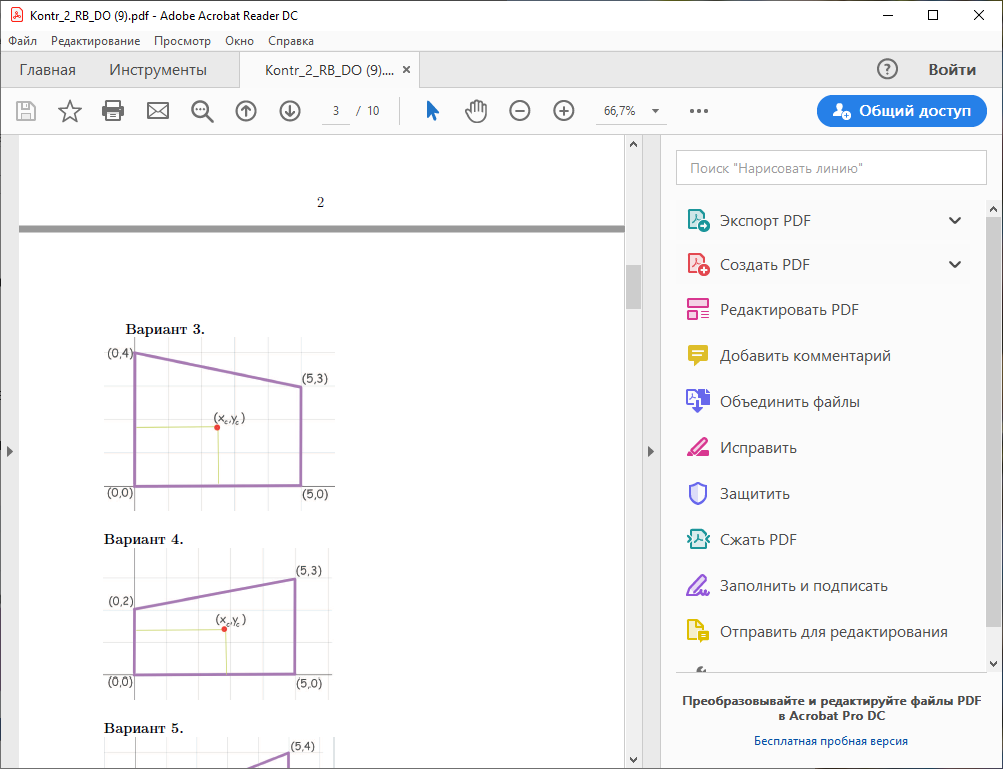
Решение: Координаты центра масс вычисляются по формуле



Так как пластина однородная, то плотность ????=????????????????????, и



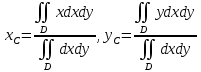
Составим уравнение прямой, ограничивающей область сверху. Для этого достаточно знать две точки 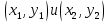,через которые она проходит: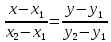



По рисунку видим, что эти две точки: (0,4) и (5,3), получаем:



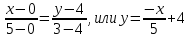
Вычислим площадь пластины (это интеграл, который фигурирует в знаменателе):





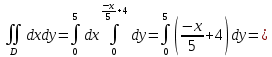
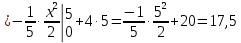
Вычислим интегралы, которые фигурируют в числителях:









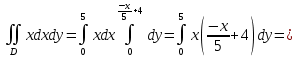
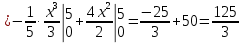
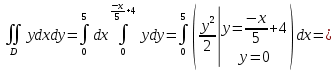
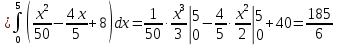
Получаем:



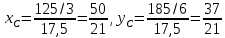
Ответ:координаты центра масс:

Задание 2. Найти общее решение дифференциального уравнения.



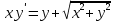
Решение.

Задано однородное дифференциальное уравнение первого порядка.Делим на х обе части уравнения:



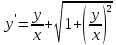
Пусть



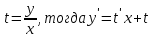
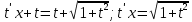
Получили уравнение с разделяющимися переменными:



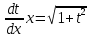
Разделяем переменные:

---

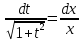
Интегрируем обе части:







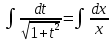
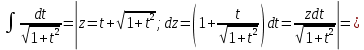
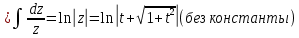
Получаем:



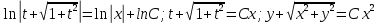
Общий интеграл дифференциального уравнения:



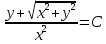
Ответ: общий интеграл:



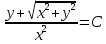
Задание 3. Найти область сходимости степенного ряда.



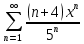
Решение.

Радиус сходимости степенного ряда вычисляем по формуле( 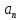–коэффициенты при степенях: ):



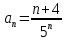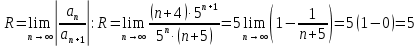
Интервал сходимости ряда: .

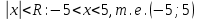Исследуем сходимость ряда на концах интервала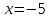. При и при 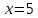получаем числовой ряд, общий член которого по абсолютной величине равен 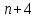,следовательно он не стремится к нулю – не выполняется необходимое условие сходимости ряда. Значит, на концах интервала сходимости ряд расходится и область сходимости степенного ряда совпадает с интервалом сходимости: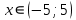



Ответ:_Задание_4.'>Ответ:

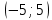
Задание 4. Вычислить с точностью до 0,001 значение определённого интеграла, разлагая подынтегральную функцию в степенной ряд.



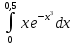
Решение.

Воспользуемся разложением в ряд Маклоренафункции :



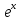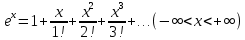
Взяв 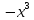вместо

---

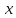, получим: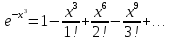



Умножив обе части уравнения на 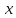,получим разложение подынтегральной функции в степенной ряд: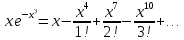



Пользуясь почленным интегрированием, получим:







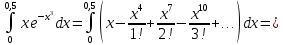
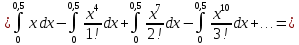
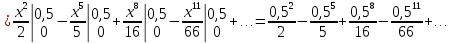
Получили сходящийся знакопеременный ряд. 3-йчлен ряда меньше 0,001 по абсолютной величине ( 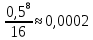), поэтому, взяв сумму первых двух членов (до 3-го), получим значение суммы ряда с точностью до 0,001: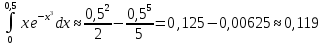



Ответ:



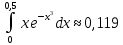
Задание 5. По заданным условиям построить область в комплексной плоскости.



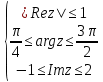
Решение.

Комплексное число: 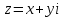,действительная часть: 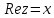, мнимая часть: .

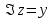Неравенство 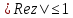равносильно 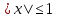– на комплексной плоскости оно определяет вертикальную полосу между прямыми .

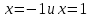Неравенство 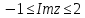равносильно 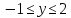– на комплексной плоскости оно определяет горизонтальную полосу между прямыми .

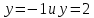Неравенство 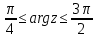определяет аргумент комплексного числа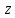

---

: из комплексной плоскости нужно исключить точки, лежащие между прямыми 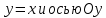в первой и 4-й координатной четвертях.

Пересечение всех указанных областей определяет нужную область – это часть прямоугольника 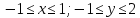,из которого исключаются точки, лежащие внутри 4-угольника с вершинами (0,0), (1,1), (1,-1), (0,-1). Все граничные точки области входят в неё, т.к. все неравенства нестрогие.

Построим эту область (она затемнена на рисунке).





























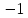
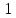
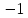
Задание 6. Вычислить значение функции комплексного переменного, результат представить в алгебраической форме.



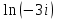
Решение.

Логарифм комплексного числа (это многозначная функция) вычисляется по формуле:



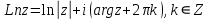
У нас: , .

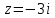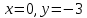Модуль числа .

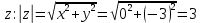Аргумент 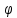числа

---

:



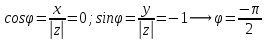
Получаем:



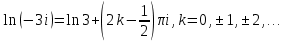
Ответ:

---

Смотрите также файлы

• высшая математика 2 задание 5.doc

• 1 Проект как объект управления.docx

• Америка, американец la Angleterre.docx

• Прогнозирование и профилактика раневых осложнений влечении послеоперационных вентральных грыж экспериментально клиническое исследование 1 Хирургия медицинские науки.pdf

• Кшм в паровых машинах 3 кшм в двигателях внутреннего сгорания 5.docx