Файл: Контрольная работа вариант 04 СанктПетербург 20 21 .docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 19
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»
(СПбГУТ)
ИНСТИТУТ НЕПРЕРЫВНОГО ОБРАЗОВАНИЯ
ЦИФРОВАЯ ОБРАБОТКА СИГНАЛОВ
КОНТРОЛЬНАЯ РАБОТА
Вариант 04
Санкт-Петербург 20_21_
| № | Коэффициенты передаточной функции | ||||
| b0 | b1 | b2 | a1 | a2 | |
| 04 | 1 | -2 | 1 | -0,88 | 0,68 |
1. Записать передаточную функцию (ПФ).
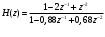
Исследуемое звено не является базовым.
2. Записать разностное уравнение (РУ).
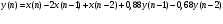
3. Изобразить структурную схему.
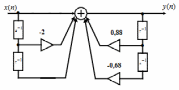
4. Записать формулу импульсной характеристики (ИХ) с учетом
нулевых начальных условий.
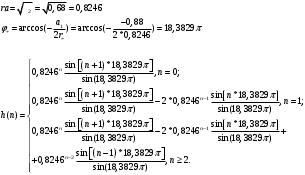
5. Рассчитать 5 отсчетов ИХ по полученной формуле с
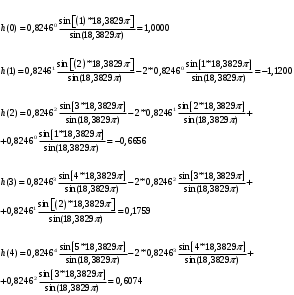
6. Рассчитать 5 отсчетов ИХ с помощью РУ с точностью до 4-го
знака после запятой.
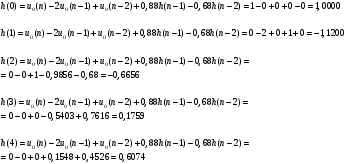
7. Сравнить результаты вычислений пп. 5, 6.
Результаты совпадают.
8. Построить график ИХ (5 отсчетов).
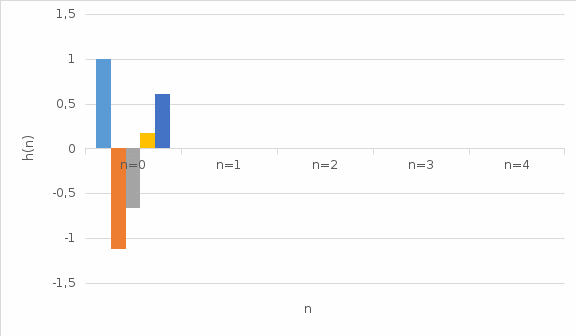
9. Изобразить карту нулей и полюсов.
Для построения карты нулей и полюсов необходимо вычислить
нули и полюсы ПФ
Комплексно-сопряженные полюсы:
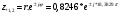
Для определения нулей умножим числитель и знаменатель ПФ на z2
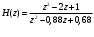
и найдем корни числителя
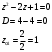
Получается один вещественный ноль
Карта нулей и полюсов
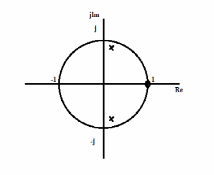
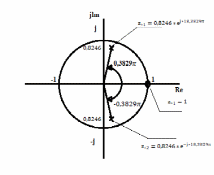
10. Записать формулы для расчета АЧХ и ФЧХ в произвольной
точке.
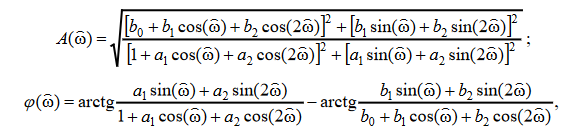
11. Сделать вывод о качественном характере АЧХ и ФЧХ по
карте нулей и полюсов.
В данном случае карта нулей и полюсов содержит два
комплексно-сопряженных полюса и один комплексно-сопряженный нуль.
В основной полосе частот
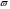∈ [0; π] АЧХ звена 2-го порядка является гладкой функцией, причем:- внутри основной полосы частот АЧХ имеет один максимум, расположенный приблизительно на частоте полюса
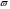∗= φ∗≈0,3829π- внутри основной полосы частот АЧХ не имеет минимума;
- на границах основной полосы частот
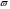=0 и = π АЧХ равна нулю; нули АЧХ не являются ее минимумами.Относительно ФЧХ можно сказать, что она представляет собой непрерывную функцию, имеющую на границах основной полосы скачки на π.
12. Выполнить экспресс-анализ АЧХ и ФЧХ.
В данном примере следует вычислить значения АЧХ и ФЧХ в четырех точках:
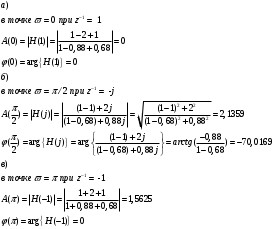
г) в точке максимума АЧХ
=
∗, который находится
приблизительно на частоте φ∗ полюса
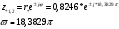
значения АЧХ и ФЧХ в этой точке, вычисленные по общим формулам соответственно, равны
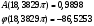
1
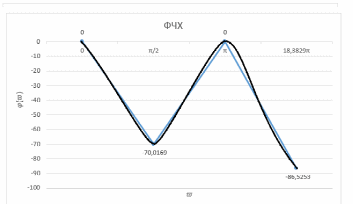
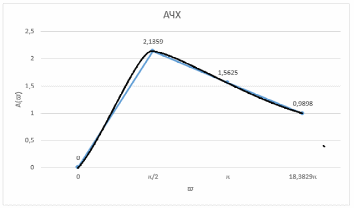3. Построить графики АЧХ и ФЧХ по результатам пп. 11 – 12.