Файл: Число это идеальная модель, точнее количество этих моделей. Множество одно из первичных понятий математики, лежащее в основе логической системы, не определяющееся через другие понятия. Такое же, как точка и прямая в геометрии. Множество.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 14
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Математика упрощает реальные объекты до идеальных моделей, отбрасывая лишнее, сосредотачиваясь на главном.
Число — это идеальная модель, точнее количество этих моделей.
Множество — одно из первичных понятий математики, лежащее в основе логической системы, не определяющееся через другие понятия. Такое же, как точка и прямая в геометрии.
Множество — это набор или совокупность элементов, объединенных каким-либо общим признаком.
Числовое множество — диапазон чисел. Когда мы говорим о видах чисел, подразумеваем, что эти числа принадлежат диапазону чисел, то есть числовому множеству.
Принадлежность к числовому диапазону обозначается символом ∈. Сами множества обозначаются заглавными латинскими буквами.
Натуральные числа — это числа, применяемые для счета предметов. Натуральные числа можно использовать в качестве номеров.
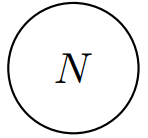Натуральные числа — это обозначение неделимых предметов «здесь и сейчас». Обозначаются символом N: N = {1, 2, 3, . . .}.Множество натуральных чисел мы можем условно изобразить вот так:
За целыми числами также скрываются исчисляемые предметы, но эти числа, уже не ограничены настоящим временем: могут описывать движение предметов во времени. Отсюда и возникает диапазон отрицательных чисел.
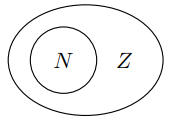Натуральные числа, им противоположные отрицательные числа и ноль вместе составляют множество целых чисел, которое обозначается Z: Z = {0, ±1, ±2, ±3, . . .}. Очевидно, множество целых чисел включает в себя множество натуральных:
Существуют предметы, которые при делении не потеряют свои свойства: вода, воздух, зерно, свет, этот список можно продолжать без конца. Возникла потребность описывать маленькие части и здесь приходят на помощь дробные числа.
Дробь — это часть, доля, выражение вида m/n, где m — целое число, n — натуральное число и n ≠ 0.
Ц
елые числа (положительные и отрицательные) также можно записать в виде дроби со знаменателем 1: . Следовательно, целые числа — частный случай дробей.
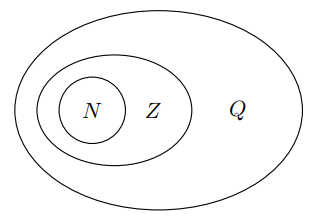Рациональные числа — это целые числа и не целые, которые можно представить в виде дроби. Рациональное число можно получить благодаря четырем арифметическим операциям: сложение, вычитание, умножение и деление.Множество рациональных чисел обозначается Q. Ясно, что оно включает в себя множество целых чисел:
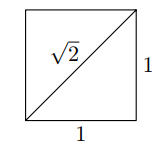Некоторые предметы зависят от других, если мы нарисуем квадрат со стороной 1, его диагональ не выражается никакой дробью вида m/n. По теореме Пифагора диагональ такого квадрата равна 
— то есть, положительному числу, квадрат которого равен двум. Это число не является рациональным. Иррациональные числа — это числа, которые нельзя выразить дробью. Обозначается символом I. К иррациональным числам также относятся число ????, число Эйлера e, золотое сечение φ, все квадратные корни натуральных чисел, кроме полных квадратов.
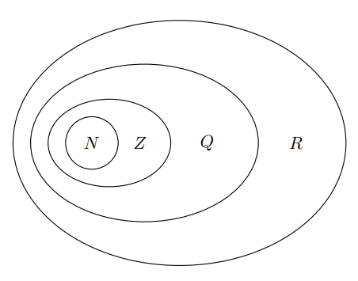Например, если в дроби 7/11 разделить в столбик 7 на 11, обнаруживается интересная закономерность: 7 : 11 = 0,636363636363... Здесь цифры повторяются, то есть дробь является периодической. Таким образом, любое рациональное число можно записать десятичной дробью — конечной или бесконечной периодической. А вот в числе 
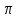= 3,1415926... цифры не заканчиваются, и никакой периодичности их следования не наблюдается. Иррациональные числа — это бесконечные непериодические дроби.Вместе оба множества — рациональных и иррациональных чисел — образуют множество действительных (или вещественных) чисел, которое обозначается R (от слова real):
Положительные и отрицательные числа симметрично расположены на числовой прямой, но при этом из положительных чисел можно извлечь квадратный корень, а из отрицательных — нельзя. Не существует действительного числа, которое при возведении в квадрат дает −1.
Оказывается, однако, что существует числовое множество, содержащее в себе множество R и бесконечное множество других чисел, не являющихся действительными. В этом множестве находится мнимая единица i, для которой верно i² = −1. И называется оно множеством комплексных чисел (С).
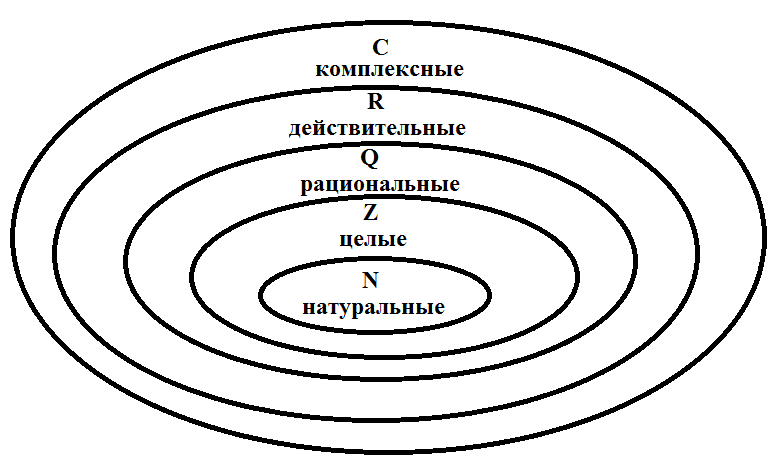Комплексные числа служат естественным языком описания многих физических явлений. В отличие от действительных («вещественных») чисел, применяемых для описания материального, плотного мира «вещей», комплексные числа оказываются удобным инструментом для построения математических моделей волн и колебаний всевозможной природы. Наукой, описывающей комплексный микромир, является квантовая физика.