ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 27
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Системы уравнения и неравенства с параметром
Линейной функцией называется функция вида y = kx + b, где k, b – некоторые числа. Графиком линейной функции является прямая линия. Коэффициент k называется угловым коэффициентом прямой, а b= у(0). Если k > 0, то функция возрастает, если k < 0, то функция убывает.
Точка лежит на прямой, если ее координаты удовлетворяют уравнению этой прямой. Например, точка М(2; 7) лежит на прямой y = 5x - 3, поскольку
7 = 5∙2 – 3 (истина).
Если точка лежит на оси абсцисс (ОХ), то ее ордината у = 0. Если точка лежит на оси ординат (ОY), то ее абсцисса х = 0.
1) Прямая y = kx + b проходит через точки (-3; -2), (1; 2). Запишите уравнение этой прямой.
▼Подставим координаты этих точек в уравнение прямой:
; 
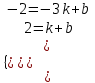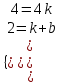k = 1, b = 1. Искомое уравнение прямой y = x + 1. Отв. y = x + 1.
Рассмотрим систему:
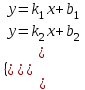, составленную из уравнений двух прямых. Две прямые y =k1x + b1 и y = k2x + b2 могут быть:а) параллельными (k1 = k2, b1 b2), система не имеет решение;
б) пересекающимися (k1 k2), система имеет одно решение;
в) совпадающими (k1 = k2, b1 = b2), система имеет бесконечно много решений.
2) При каких значениях параметра а система
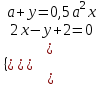: а) имеет единственное решение; б) не имеет решения; в) имеет бесконечно много решений.▼ Выразим в каждом уравнении системы переменную у:
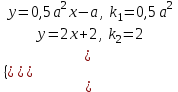
Система имеет единственное решение, если k1 k2, 0,5a2 2, a2 4, a 2.
Если k1 = k2, то прямые могут либо совпадать, либо быть параллельными.
При а = 2 имеем систему
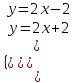и прямые параллельные, система не имеет решения.При а = -2 имеем систему
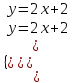и прямые совпадают, система имеет бесконечно много решений.Отв. при a 2 единственное решение; при а = 2 нет решения; при а = -2 бесконечно много решений.
Пусть коэффициенты уравнений системы
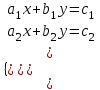отличны от нуля, тогда:а) если
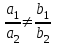, то система имеет единственное решение;б) если
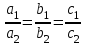, то система имеет бесконечно много решений;в) если
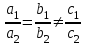, то система не имеет решений.Случай, когда некоторые коэффициенты равны нулю, нужно рассматривать отдельно; например, если
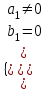, или 
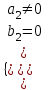, то система имеет единственное решение.Упр.
1) Определить, при каком значении а система
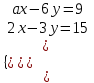не имеет решения.▼
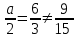а = 4. Отв. а = 4.2) Определить, при каком значении а система
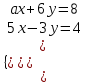имеет бесконечно много решений.▼
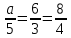а = 10. Отв. а = 10.3) Определить, при каком значении а система
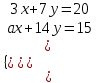имеет единственное решение.▼
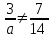а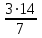 
= 6. Отв. а 6.4) Определить все значения а, при которых система
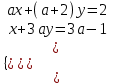имеет единственное решение.▼
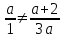, 3а2 а + 2, а 1; - 2/3. Отв. при а 1; - 2/3.5) Определить все значения а, при которых система
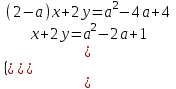
имеет бесконечно много решений.
▼Система имеет бесконечно много решений, если
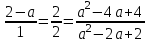. Поскольку уравнение 
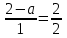имеет единственный корень а = 1, и при а = 1 выполняется равенство 
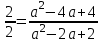, то система имеет бесконечно много решений при а = 1.Отв. при а = 1.
6) Для каждого значения параметра а укажите количество решений (х; у) системы уравнений
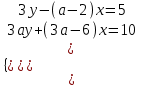
▼При а = 0 система принимает вид
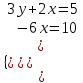и, очевидно, имеет одно решение. При а 0 получаем систему
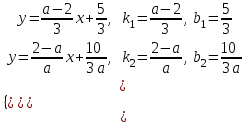.Эта система может: а) не иметь решений; б) иметь бесконечно много решений; в) иметь единственное решение.
а)
; 
; 
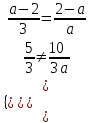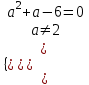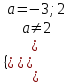, а = -3.б)
; 
; 
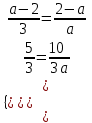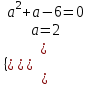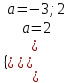, а = 2.в)
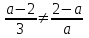, a2 + a – 6 0, a -3; 2.Отв. при а = -3 решений нет; при а = 2 бесконечно много решений; при
a -3; 2 и при а = 0 единственное решение.
7) Исследовать систему уравнений
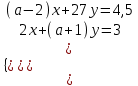
▼Определим значение параметра а, при которых
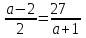. Это возможно, если 
; 
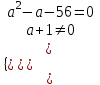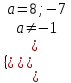, т.е. при a = 8; -7.Если a = 8 или a = -7, то решений нет, т.к.
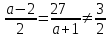
При a 8 и a -7 существует единственное решение
(х, у) = (
;
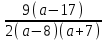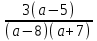).Отв. при a = 8 или a = -7 решений нет; при a
8; -7 (х, у) = (
;
).8) При каких а система
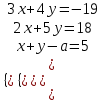имеет решение.▼ Эти три уравнения – уравнения прямых. Чтобы система имела решения, нужно, чтобы все три прямые пересекались в одной точке.
Сначала найдем координаты пересечения первых двух прямых:
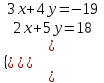(х; у) = (-1; -4).Подставим координаты (-1; -4) в третье уравнение: -1 – 4 – а = 5, а = -10.
Отв. а = -10.
9) Для каждого значения а решить систему уравнений
▼
; 
; 
=
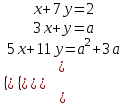
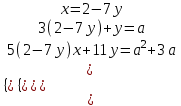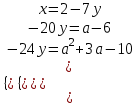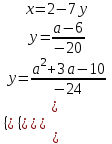
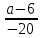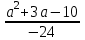, 5a2 + 9a – 14 = 0, 
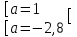.При
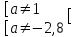решений нет.Пусть а = 1, тогда у =
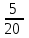= 0,25, х = 2 - 7∙0,25 = 0,25.Пусть а = -2,8, тогда у =
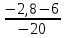= 0,44, х = 2 - 7∙0,44 = -1,08.Отв. при а = 1, (х, у) = (0,25; 0,25); при а = -2,8, (х, у) = (-1,08; 0,44); при
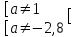решений нет.10) При каких а система
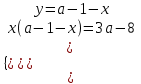имеет единственное решение.▼ Исходная система имеет единственное решение, если уравнение x2 - (a –
-1)x + 3a – 8 = 0 имеет единственное решение. Это возможно, если D = 0.
D = (a –1)2 – 4(3a – 8) = a2 – 14a + 33 = 0,
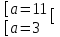, тогда x1 = x2 =
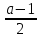.При а = 11, х = 5, у = 5, решение (5; 5).
При а = 3, х = 1, у = 1, решение (1; 1).
Отв. при а = 3; 11 система имеет единственное решение.
11) При каких а система
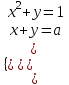
имеет одно решение.
▼ Исходная система имеет одно решение, если уравнение x2 + (a – х) = 1,
x2 – х + а – 1 = 0 имеет одно решение. Это возможно, если D = 0.
D = 1 - 4(a –1) = 0, 4а = 5, а = 1,25.
Отв. 1,25
12) Решите систему неравенств
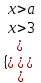
▼ Сравним взаимное расположение точек а и 3 на координатной прямой.
Рассмотрим три случая: а) а = 3; б) а < 3; в) а > 3.
а) а = 3, х > 3.
б) а < 3, х > 3.
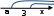
в) а > 3, х > а.
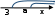
Отв. при а 3, х > 3; при а > 3, х > а.
13) Решите систему неравенств
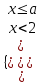
▼ Сравним взаимное расположение точек а и 2 на координатной прямой.
Рассмотрим случаи:
а) а = 2, х < 2.
б) а > 2, х < 2.
в) а < 2, х а.
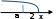
Отв. при а < 2, х а; при а 2, х < 2.
14) При каких значениях параметра а система
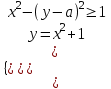имеет хотя бы одно решение.▼ Из уравнения системы выразим х2 через у и подставим в неравенство
; 
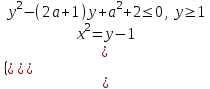
Введем функцию f(y) =
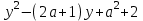, y 1.Для того, чтобы неравенство f(y) 0, где y 1, имело хотя бы одно решение, график функции f(y) должен располагаться так, как указано на рисунке
        y1 1 y0 y2 |