ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 46
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Квадратные уравнения с параметрами
Уравнения вида ax2 + bx + c = 0, где a, b, c – выражения, зависящие от параметров, a 0, x – неизвестное, называется квадратным уравнением с параметрами.
I. Число корней квадратного уравнения определяется
по знаку детерминанта
Схема исследования
1) При а = 0 имеем линейное уравнение bx + c = 0
2) При а 0 в зависимости от знака дискриминанта D имеем:
а) D > 0, уравнение имеет два различных корня;
б) D = 0, уравнение имеет один корень кратности 2;
в) D < 0, уравнение не имеет действительных корней.
1) Найти все значения параметра а, для которых уравнение
(a - 1)x2 + 2(2a + 1)x + 4a + 3 = 0 имеет: а) два различных корня; б) один корень; в) не имеет корней.
▼ При a – 1 = 0, a = 1, 6x + 7 = 0, x = -7/6 – один корень.
При a 1 имеем квадратное уравнение.
D = 4(2a + 1)2 – 4(a - 1)(4a + 3) = 4(5a + 4)
а) D > 0, 5a + 4 > 0, a > -4/5 (два корня)
б) D = 0, 5a + 4 = 0, a = -4/5 (один корень)
в) D < 0, 5a + 4 < 0, a < -4/5 (нет корней)
Отв. при a > -4/5 и a 1 два корня; при a = -4/5; 1 - один корень; при a < -4/5 нет корней.
2) При каких значениях параметра а уравнение x2 + x +
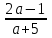= 0 не имеет корней.▼ ОДЗ: a + 5 0, a -5
Пусть a -5. Квадратное уравнение не имеет решения, когда D < 0
D = 1 – 4(
) =
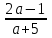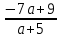< 0, (a- 9/7)(a + 5) > 0Отв. (-;-5)(9/7; )
II. Применение теоремы Виета
Теорема Виета. Если квадратное уравнение ax2 + bx + c = 0, a 0 с дискриминантом D 0 имеет корни х1 и х2, то
х1 + х2 = -
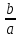
х1х2 =
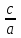
Следствие. Квадратное уравнение имеет:
а) действительные корни (равные или различные), если D 0
б) корни одинакового знака, если
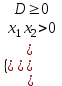;в) два положительных корня, если
;
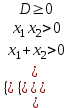
г) два отрицательных корня, если
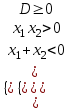;д) корни разных знаков, если
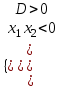(условие D > 0 автоматически выполняется), при этом положительный корень больше модуля отрицательного, если х1 + х2 > 0;
положительный корень меньше модуля отрицательного, если х1 + х2 < 0.
Полезные равенства:
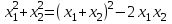
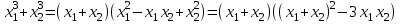
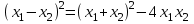
1) При каких значениях параметра а оба корня квадратного уравнения
(a - 2)x2 + 8x + a + 4 = 0 будут: а) действительны; б) одинакового знака;
в) положительными; г) разного знака.
▼ Поскольку уравнение квадратное, а – 2 0, а 2.
D = 64 - 4(a - 2)(a + 4) =- 4(a2 + 2a - 24)
а) Корни действительны, если D 0, =- 4(a2 + 2a - 24) 0,
a2 + 2a - 24 0, (a + 6)(a- 4) 0, -6 a 4
б) корни одинакового знака, если
, 
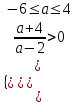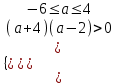, a-6;-4)(2; 4в) Корни положительны, если
, 
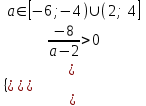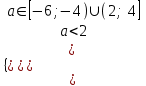, a-6;-4)г) Корни разных знаков, если х1х2 < 0,
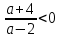, (a + 4)(a- 2) < 0,-4 < a < 2, a(-4; 2)
2) При каких значениях параметра а уравнение x2 - 2(а - 1)x + a + 5 = 0 имеет: а) различные действительные корни; б) различные положительные корни; в) различные отрицательные корни; г) корни разных знаков; д) совпадающие корни.
▼ D = (a - 1)2 - (a + 5) = a2 - 3a – 4
а) Действительные корни различны, если D > 0
a2 - 3a – 4 > 0, (a+ 1)(a - 4) > 0, a(-;-1)(4; )
б) Различные корни положительны, если
, 
, 
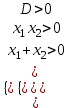
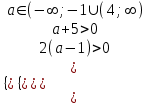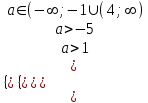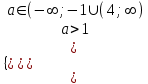; a > 4в) Различные корни отрицательны, если
, 
, 
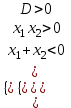
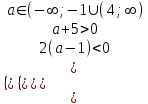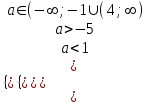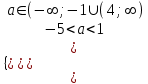; -5 < a < -1г) Корни разных знаков, если х1х2 < 0, a+ 5 < 0, a < -5
д) Кори совпадающие, если D = 0, a2 - 3a – 4 = 0, a = -1; 4
3) Найти все значения параметра а, при котором разность корней уравнения x2 + аx + 12 = 0 равна 1.
▼ D = a2 – 48 > 0
Пусть х1, х2 – корни исходного уравнения, тогда
, 
, 
, 
, 
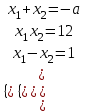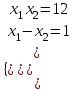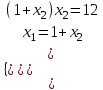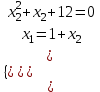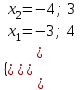
а = -( х1+ х2) = 7; -7. Условие D = a2 – 48 = 49 – 48 = 1 выполнено. Отв. 7
4) Найти все значения параметра а, при каждом из которых уравнение
x2 - 8x + 5а = 0 и 2x2 + x - 7а = 0 имеют хотя бы один общий корень.
▼ Составим систему и решаем
, 
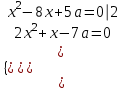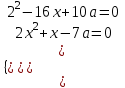, -17х + 17а = 0, х = аПодставим х = а в любой из исходных уравнений, получим
а2 - 8а + 5а = 0, а2 - 3а = 0, а(а – 3) = 0, а = 0; 3. Отв. 0; 3.
III. Расположение корней квадратного уравнения
относительно заданных чисел
Пусть х1, х2 (х1 х2) – корни квадратного трехчлена f(x) = ax2 + bx + c
(a 0), D = b2 – 4ac, x0 = -
=
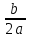
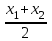- вершина параболы.Расположение корней х1, х2 относительно заданного числа М али интервала (A; B) сводится к необходимым и достаточным условиям реализации одного или несколько следующих случаев.
1) Оба корня меньше числа М: х1 х2 < M
a > 0:
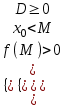; a < 0: 
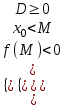; или 
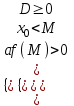
| a > 0 | a < 0 |
          M  x0 x2 x1 |      M x2 x0 x1 |
2) Оба корня больше числа М: M < х1 х2
a > 0:
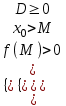; a < 0: 
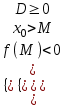; или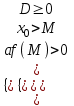 
| a > 0 | a < 0 |
        x1 M x0 x2 |      x0 x1 x2 M |