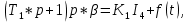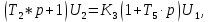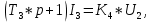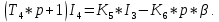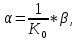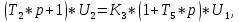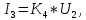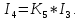Файл: Курсовой проект по дисциплине Теория автоматического управления.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 35
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ.ПРОФ.М.А.БОНЧ-БРУЕВИЧА» (СПбГУТ)
Факультет «Информационных систем и технологий»
Кафедра «Интеллектуальных систем автоматизации и управления»
| Направление подготовки: 27.03.04 Управление в технических системах |
| Направленность (профиль): Информационные технологии в управлении |
Курсовой проект
по дисциплине:
| Теория автоматического управления |
| | | Выполнил студент группы УБ-01з | | |
| | | Хамидов Саид Хусейнович | ||
| | | Фамилия И. О. | ||
| | | | | |
| оценка | | | уч. степень, уч. звание | |
| | | | ||
| дата, подпись | | Фамилия И. О. | ||
Санкт-Петербург
2023
СОДЕРЖАНИЕ
ИСХОДНЫЕ ДАННЫЕ 3
ЧАСТЬ I 4
§1 Следящая система 4
ЧАСТЬ II 6
§1 Уравнения звеньев системы 6
§2 Передаточные функции звеньев системы 10
§3 Приведение системы уравнений по звеньям к единому дифференциальному уравнению 11
Часть 3 13
§1 Получение уравнения статики системы и его использование при расчете системы 13
§2 Проверка системы на устойчивость 14
§3 Проверка САУ на устойчивость по методу Гурвица 17
§4 Проверка САУ на устойчивость по методу Рауса 18
§5 Проверка САУ на устойчивость по методу Михайлова 19
ВЫВОД: 21
ИСХОДНЫЕ ДАННЫЕ
Т1 = 0,6 с;
Т2 = 1 c
γ = 11 угл. мин;
α = 2 рад/с.
ЧАСТЬ I
§1 Следящая система
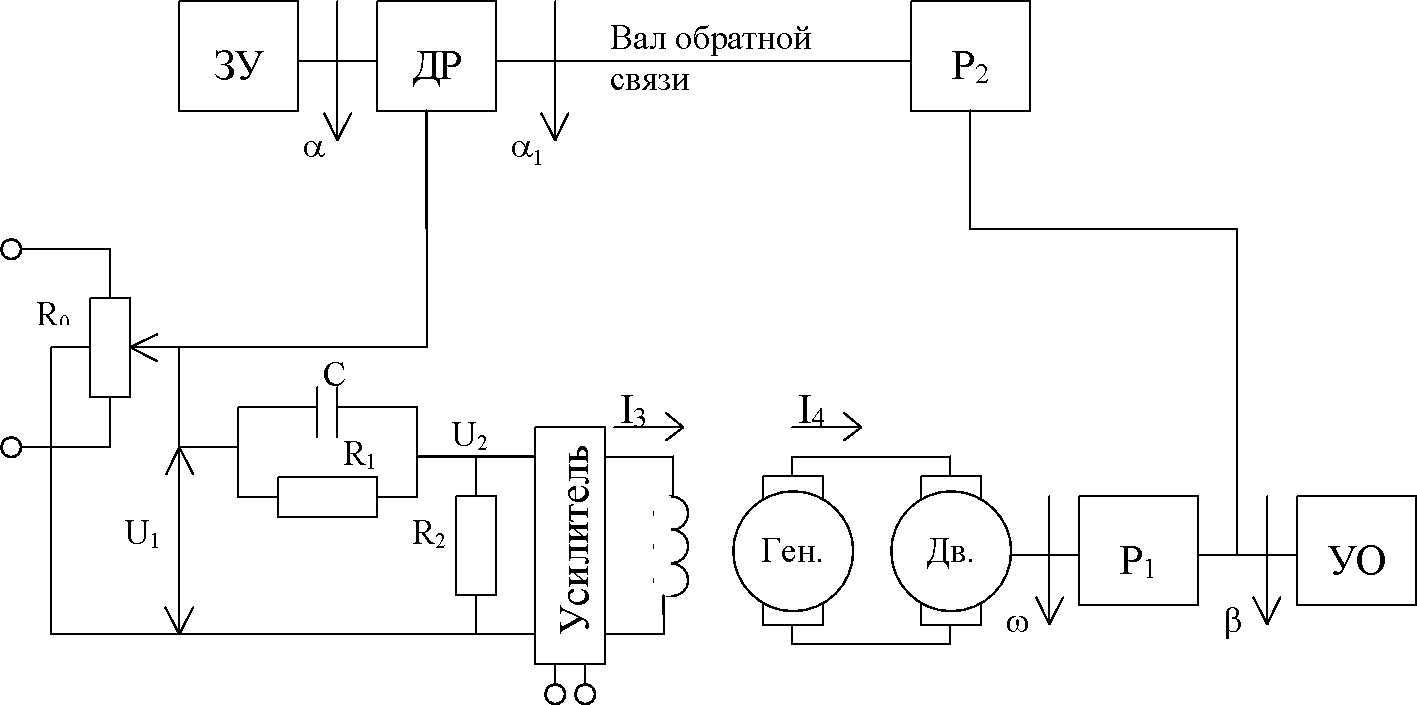
Рис. 1 Функциональная схема следящей системы.
ЗУ – задающее устройство;
R0 – потенциометр;
Ген. – генератор;
Дв. – двигатель;
Р1, Р2 – редукторы;
ДР – датчик рассогласования;
УО – управляемый объект.
Краткое описание системы
Система предназначена для слежения в постоянном масштабе вала управляемого объекта за задающим валом. Механический дифференциал выполняет функцию датчика рассогласования, сравнивая углы поворота вала задающего устройства α и вала обратной связи α1, полученное рассогласование
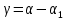 с помощью потенциометра преобразуется в напряжение U1, которое подается на вход дифференцируемого контура, состоящего из емкости и сопротивлений R1 и R2. Усиленный усилителем ток I3, поступает на обмотку возбуждающего генератора, цепь якоря которого последовательно соединена с цепью якоря двигателя постоянного тока с независимым возбуждением. Двигатель через редуктор Р1 поворачивает вал управляемого объекта на угол
с помощью потенциометра преобразуется в напряжение U1, которое подается на вход дифференцируемого контура, состоящего из емкости и сопротивлений R1 и R2. Усиленный усилителем ток I3, поступает на обмотку возбуждающего генератора, цепь якоря которого последовательно соединена с цепью якоря двигателя постоянного тока с независимым возбуждением. Двигатель через редуктор Р1 поворачивает вал управляемого объекта на угол 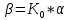 . Т.к. датчик рассогласования должен сравнивать величину одного масштаба в цепь обратной связи включен редуктор Р2, задача которого изменение масштаба угла β в
. Т.к. датчик рассогласования должен сравнивать величину одного масштаба в цепь обратной связи включен редуктор Р2, задача которого изменение масштаба угла β в 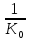 раз.
раз.ЧАСТЬ II
§1 Уравнения звеньев системы
-
Уравнение управляемого объекта с двигателем.
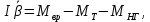
I – приведенный к валу объекта момент инерции всех масс, связанных с этим валом;
Мвр – вращающий момент на валу объекта;
МТ – момент сил трения и сопротивления;
МНГ – момент внешней нагрузки на объект.
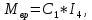
I4 – ток цепи якоря двигателя.
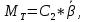
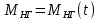 – уравнение объекта с двигателем в стандартной форме.
– уравнение объекта с двигателем в стандартной форме.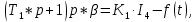
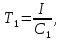
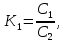
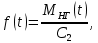
-
Уравнение обратной связи.
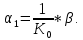
-
Уравнение датчика рассогласования.
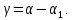
-
Уравнение потенциометра.
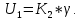
-
Уравнение дифференцирующего контура.
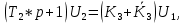
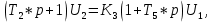
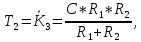
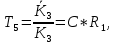
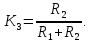
Полезный сигнал дифференцирующего контура характеризуется правой частью уравнения, постоянная времени Т2 определяет методическую ошибку при дифференцировании.
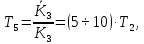
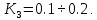
-
Уравнение усилителя и цепи возбуждения генератора.
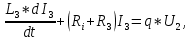
L3 и R3 – индуктивность и сопротивление обмотки возбуждающего генератора;
Ri – внутреннее сопротивление лампы усилителя;
I3 – ток в цепи обмотки возбуждающего генератора;
q – коэффициент усиления;
В стандартной форме принимает вид:
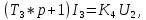
Где
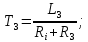
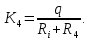
-
Уравнение цепи якорей генератора и двигателя.
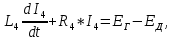
L4, R4 – индуктивность и сопротивление цепи якорей;
I4 – ток в цепи якорей;
ЕГ – ЭДС генератора;
ЕД – противо ЭДС двигателя.
Считая, что
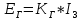 и
и 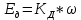 (или с учетом уравнения редуктора
(или с учетом уравнения редуктора 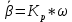 ),
), 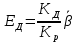 принимает вид:
принимает вид: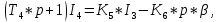
Где:
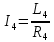 ;
; 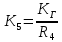 ;
; 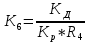 .
.Противо ЭДС двигателя играет роль дополнительной отрицательной обратной связи. Единое уравнение получено путем решения системы уравнений звеньев относительно рассогласования γ и задающего воздействия α.
При этом
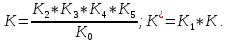
Система уравнений имеет вид:
Учитывая заданные параметры:
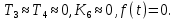
Получим:
§2 Передаточные функции звеньев системы
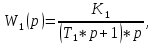
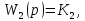
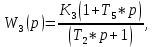
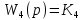 ,
,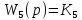 ,
,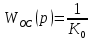 .
.Т.к. в следящей системе отсутствуют внешние воздействия, то передаточные функции полностью отражают систему.
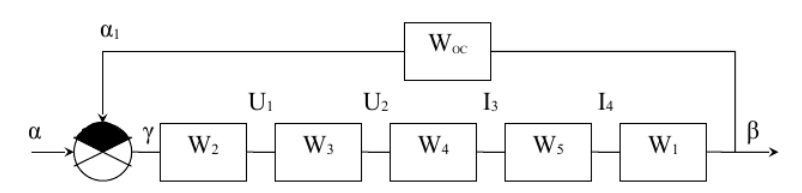
Рис. 2. Структурная схема САУ
§3 Приведение системы уравнений по звеньям к единому дифференциальному уравнению
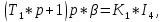
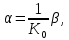
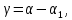
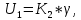
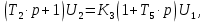
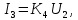
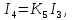
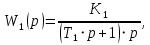
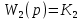 ,
,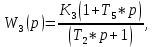
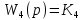 ,
,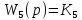 .
.Для того чтобы вывести единого уравнения требуется решить дифференциальные уравнения относительно рассогласования
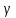 и задающего воздействия
и задающего воздействия 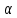 .
.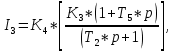
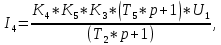
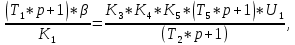
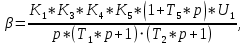
Так как
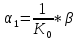 , то
, то 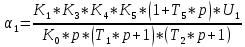 ,
,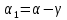 ,
,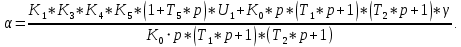
Единое уравнение системы:
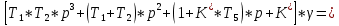
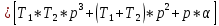 ,
,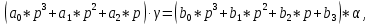
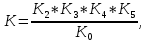
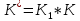 .
.Передаточная функция замкнутой системы и ее разомкнутой цепи:
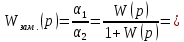
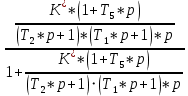 =
= 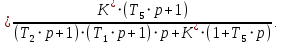
Передаточная функция по ошибке:
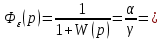
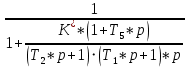 =
=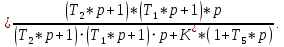
Передаточная функция разомкнутой цепи:
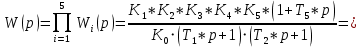
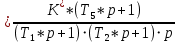 .
.Часть 3
§1 Получение уравнения статики системы и его использование при расчете системы
Уравнение следящей системы:
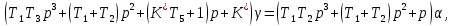
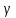 – угол рассогласования входного и выходного валов,
– угол рассогласования входного и выходного валов,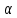 – угол поворота входного вала.
– угол поворота входного вала.Искомыми параметрами являются коэффициент усиления
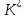 и постоянная времени дифференциального контура
и постоянная времени дифференциального контура 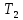 .
. За статический режим следящей системы принимаем установившийся режим слежения за выходным валом, вращающимся с постоянной скоростью
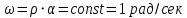 .
.Подставив в исходное уравнение значения, получим уравнение статики:
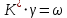 ,
, 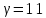
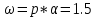
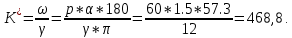
§2 Проверка системы на устойчивость
Так как наша следящая система описывается уравнением третьего порядка, то для её исследования на устойчивость удобно пользоваться критерием Вышнеградского, по которому для устойчивости линейной системы необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были положительны и произведение средних коэффициентов было бы больше произведения крайних.
Построение границы устойчивости.
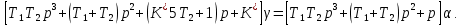
Общий вид:
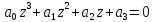 .
.где
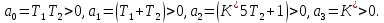
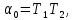
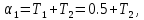
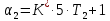 ,
,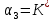 .
.Система находится на границе устойчивости, если:
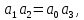
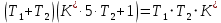
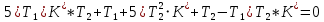
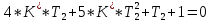
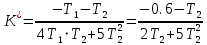
Построим график
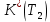 :
: Таблица№ 1
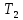 | 0.1 | 0.5 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
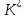 | -2,8 | -0,48 | -0,23 | -0,11 | -0,07 | -0,05 | -0,04 | -0,03 | -0,03 | -0,03 |
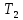 | 9 | 10 |
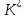 | -0.02 | -0.02 |
Пример расчета при
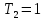 :
: 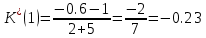
Если
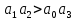 – система устойчива.
– система устойчива.Если
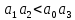 – система неустойчива.
– система неустойчива.Рассмотрим точки А (0.5; -0.1) и B (1; -1).
Для А (0.5; -0.1):
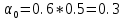 ,
,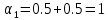 .1,
.1,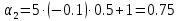 ,
,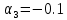 ,
,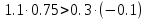 ,
,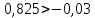 (Система устойчива).
(Система устойчива).Для B (1; -1):
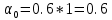 ,
,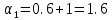 ,
,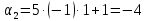 ,
,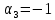 ,
,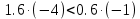 ,
,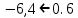 (Система неустойчива).
(Система неустойчива).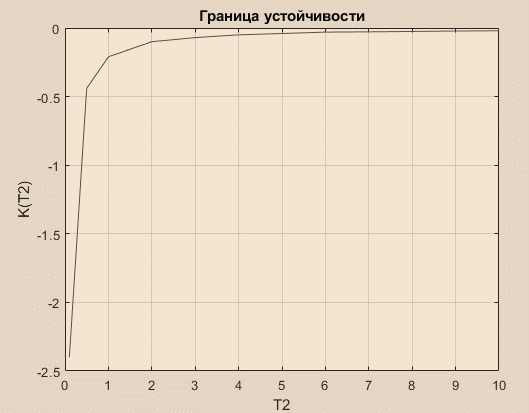
§3 Проверка САУ на устойчивость по методу Гурвица
Чтобы САУ была устойчива необходимо и достаточно, чтобы все определители Гурвица имели одинаковые знаки со знаком первого коэффициента
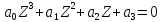 .
.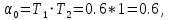
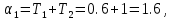
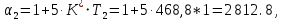
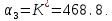
Т.е. при
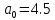 были положительны.
были положительны.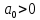 ,
, 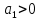 ,
, 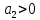 ,
, 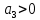 .
.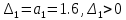 ,
,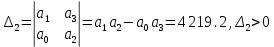 ,
,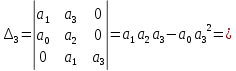
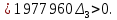
Т.к.
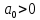 , то для устойчивости САУ нужно, чтобы
, то для устойчивости САУ нужно, чтобы 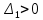 ,
, 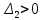 ,
,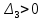 . Все главные определителя Гурвицы положительны при
. Все главные определителя Гурвицы положительны при 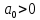 , следовательно согласно критерию Гурвица САУ устойчива.
, следовательно согласно критерию Гурвица САУ устойчива.§4 Проверка САУ на устойчивость по методу Рауса
Для устойчивости САУ необходимо и достаточно, чтобы коэффициенты первого столбца таблицы Рауса имели тот же знак, что и a0.
Заполним таблицу Рауса (таблица №5). Коэффициенты таблицы определяем согласно формулам:
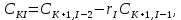
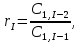
где
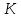 - номер столбца,
- номер столбца,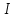 -номер строки.
-номер строки.Таблица №5
| | Строки | Столбцы | |
| 1 | 2 | ||
| … | 1 | 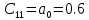 | 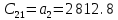 |
| … | 2 | 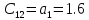 | 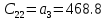 |
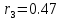 | 3 | 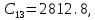 | 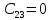 |
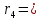 0,000496 | 4 | 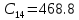 | 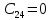 |
Т.к.
 , то нужно, чтобы
, то нужно, чтобы 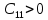 ,
, 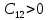 ,
, 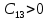 ,
,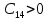 .
.Все коэффициенты первого столбца положительны, следовательно, согласно критерию Рауса САУ устойчива.
§5 Проверка САУ на устойчивость по методу Михайлова
Для устойчивости системы достаточно и необходимо, чтобы годограф Михайлова, при изменении ω от 0 до ∞, начинался на вещественной положительной полуоси X(ω) и обходил против часовой стрелки n квадрантов, гдe n – степень уравнения.
Характеристический полином:
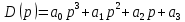 ,
,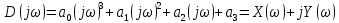 .
.Вещественная функция Михайлова:
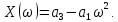
Мнимая функция Михайлова:
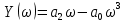 .
.САУ устойчива тогда и только тогда, когда X(w) и Y(w) имеют все действительные и перемежающиеся корни. Причем общее число этих корней равно трем, т.е порядку характеристического уравнения и при w = 0 удовлетворяет условию
X(0) > 0
Y(0) > 0
Корнем X(w) является
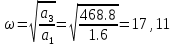
Корнем Y(w) является
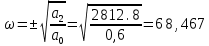
Т.к. по определению ???? > 0, то корнями Y(????) являются ???? =
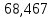 ; ???? = 0.
; ???? = 0.Условия для ???? > 0 имеют вид:
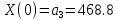
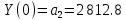
Все условия для критерия Михайлова выполняются, следовательно система является устойчивой.
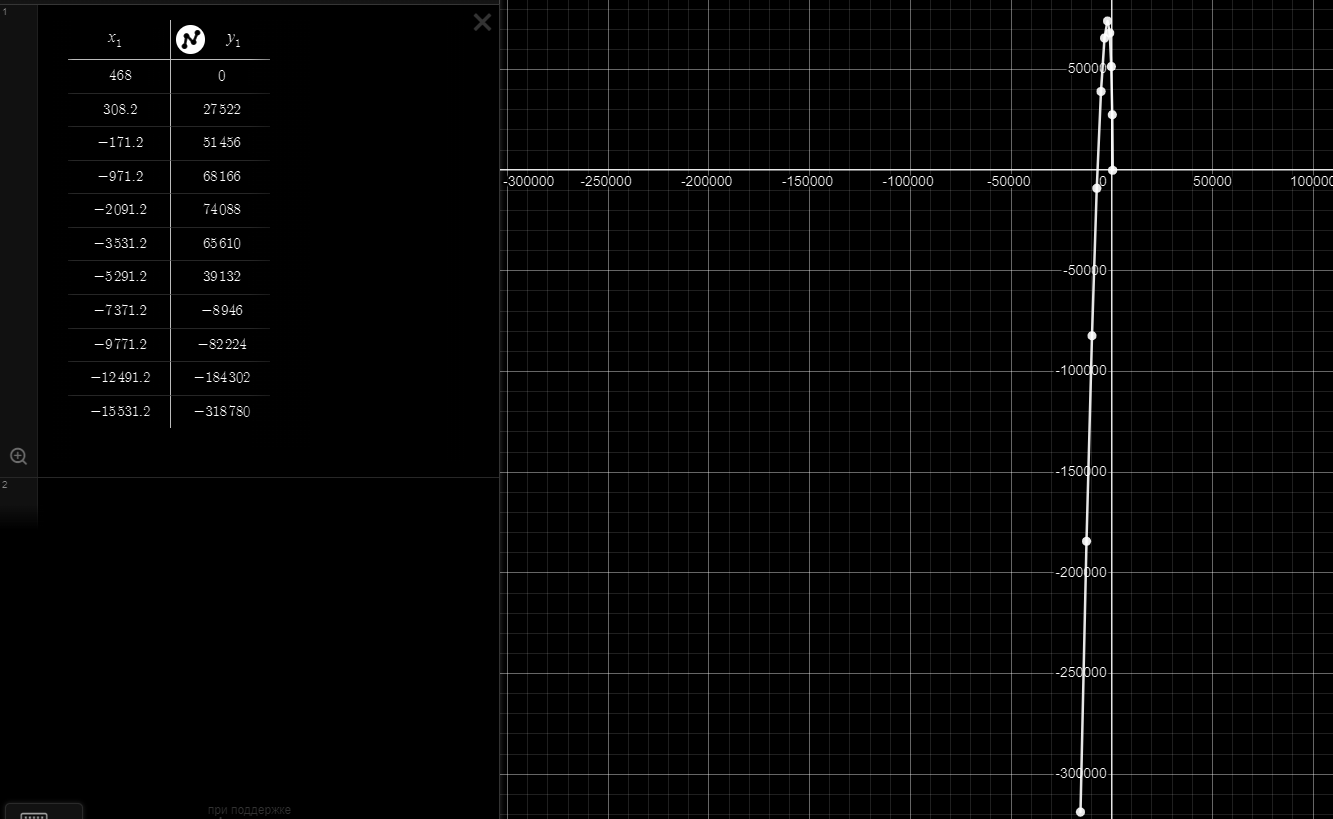
Годограф Михайлова:
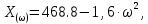
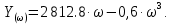
Построим годограф Михайлова:
Таблица №6
| ω, рад/с | X(ω) | Y(ω) |
| 0 | 468,8 | 0 |
| 10 | 308,8 | 27522 |
| 20 | -171,2 | 51456 |
| 30 | -971,2 | 68166 |
| 40 | -2091,2 | 74088 |
| 50 | -3531,2 | 65610 |
| 60 | -5291,2 | 39132 |
| 70 | -7371,2 | -8946 |
| 80 | -9771,2 | -82224 |
| 90 | -12491,2 | -184302 |
| 100 | -15531,2 | -318780 |
Пример расчета при
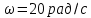 :
: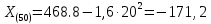
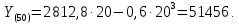
САУ по критерию Михайлова является устойчивой, так как годограф обходит 3 квадранта и начинается на вещественной положительной полуоси.
ВЫВОД:
В данном курсовом проекте была исследована динамика следящей системы, из условия обеспечения допустимой скоростной ошибки был найден общий коэффициент усиления САУ. Из условия обеспечения устойчивости было найдено значение T2 — постоянная времени дифференцирующего контура. Также САУ исследована на устойчивость по критериям: Рауса, Гурвица, Михайлова — по всем критериям система устойчива.