Файл: Контрольная работа по теме Базы данных в Excel 72 IV. Макросы в ms excel 78 Макросы для автоматизации работ 78.doc

6.8.3. Пример

Пусть процесс описывается следующей системой уравнений:

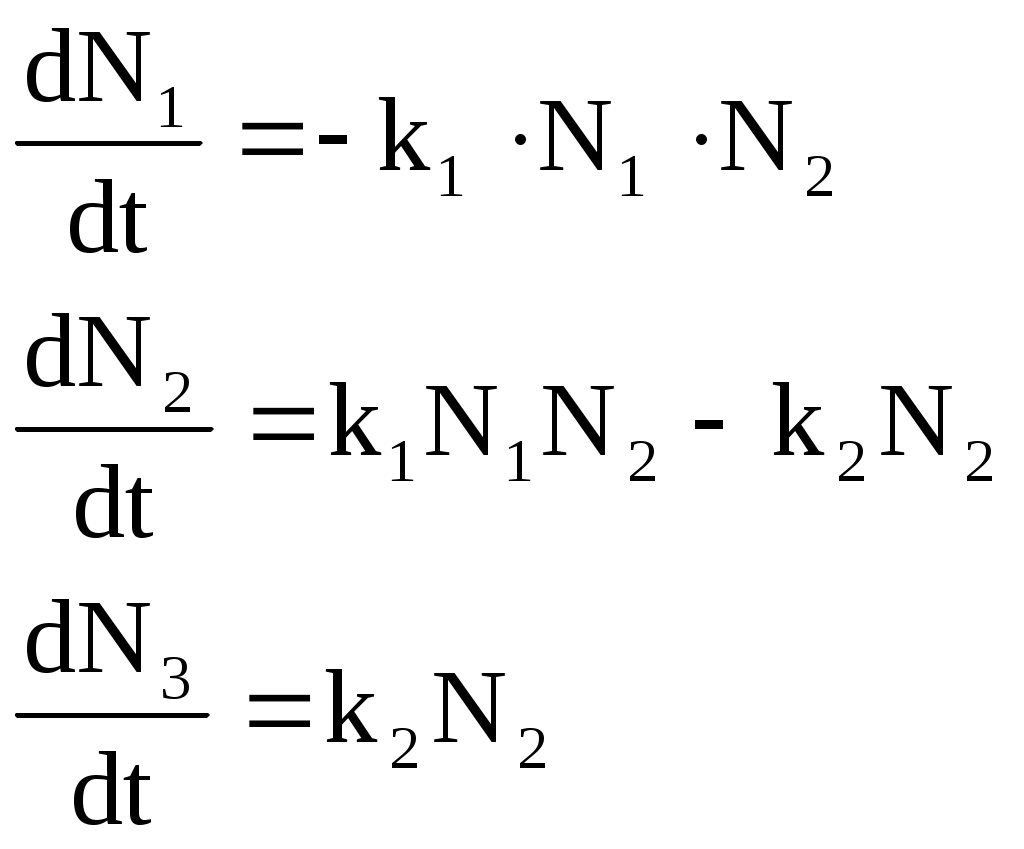
Значения переменных в начальный момент времени: N₁=100, N₂=1, N₃=0. Значения параметров уравнения: k₁=0.5, k₂=4.

Необходимо изучить поведение процесса.

Решения состоит из следующих этапов:

1. 
   Загрузить файл Diffur.xls.
   
2. 
   Вызвать редактор Visual Basic и в нем вызвать макрос “Systema”
   
3. 
   В макросе уже прописано дифференциальное уравнение следующего вида:
   

Private Sub Systema()

F(1) = k1 * N(1) - k2 * N(1) * N(2)

F(2) = -k3 * N(2) + k4 * N(1) * N(2)

F(3) = 0

End Sub

4. Исправить данный макрос, вписав в него уравнения, соответствующие заданию:

Private Sub Systema()

F(1) = - k1 * N(1) * N(2)

F(2) = k1 *N(1)* N(2) – k2 * N(2)

F(3) = k2*N(2)

End Sub

5. Вернуться в Excel и вписать:

– в поля «Начальные значения»:

Начальные значения
N1	100
N2	1
N3	0

– в поля «Время» и «Интервал»:

Время	1
Интервал	0,001

– в поля «Параметры уравнения»:

Параметры уравнения
k1	0,5
k2	4
k3
k4
k5
k6

Примечания.

а) Подбор параметров расчетов дело очень непростое.

Здесь требуется «почувствовать» моделируемый процесс и представить, как он должен протекать. Исходя из своих представлений процесса и подбираются указанные выше параметры.

б) Особую роль играет параметр «Интервал». Его значение зависит от вида уравнений, их коэффициентов и времени. Чем меньше значение интервала, тем точнее производятся расчеты. Его минимальная величина определяется балансом между временем расчетов и их точностью.

---

6. Щелкнуть по кнопке «Расчет». В результате выполнения макроса таблица расчетов заполнится данными и на их основе будет построен график вида (рис. 6.5):



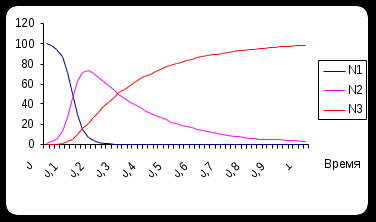
Рис. 6.5. Графическое представление результатов расчетов задачи о коньюнктуре
Главное требование к результатам расчетов:

Результаты должны отражать основные закономерности процесса
Недопустимы результаты, показывающие только начальную или только конечную стадию процесса. Для рассматриваемого примера это могут быть рисунки типа (рис. 6.6, 6.7):


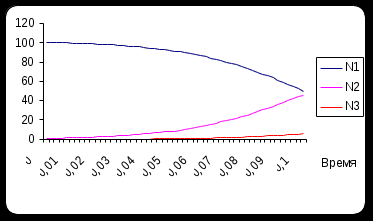
Рис. 6.6. Графическое представление результатов расчетов задачи о конъюнктуре

при задании малого времени протекания процесса
или



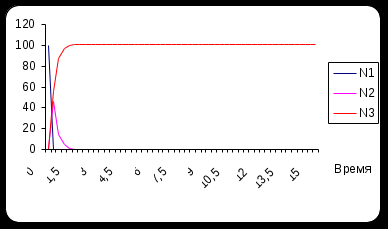
Рис. 6.7. Графическое представление результатов расчетов задачи о конъюнктуре

при задании чрезмерно большого времени протекания процесса
6.8.4. Варианты заданий

1. 
   Производство в условиях постоянного спроса
   

Пусть имеется постоянный и устойчивый спрос на некоторое условное изделие – N_max. В таких условиях динамика объема производства этих изделий (N) будет описываться с помощью уравнения:

,
где k – некоторый коэффициент пропорциональности;

N – текущий объем производства;

N_max – максимальный спрос на изделие.

Построить на одном рисунке зависимости N – t при различном начальном объеме выпуска изделий.

Указание

При вводе уравнения в программу вместо N_max следует указывать конкретное число.

2. 
   Конкуренция
   

Предположим, что некоторое изделие с постоянной величиной спроса выпускается двумя фирмами. Тогда динамика производства этого изделия каждой фирмой будет описываться следующей системой уравнений:

---

,
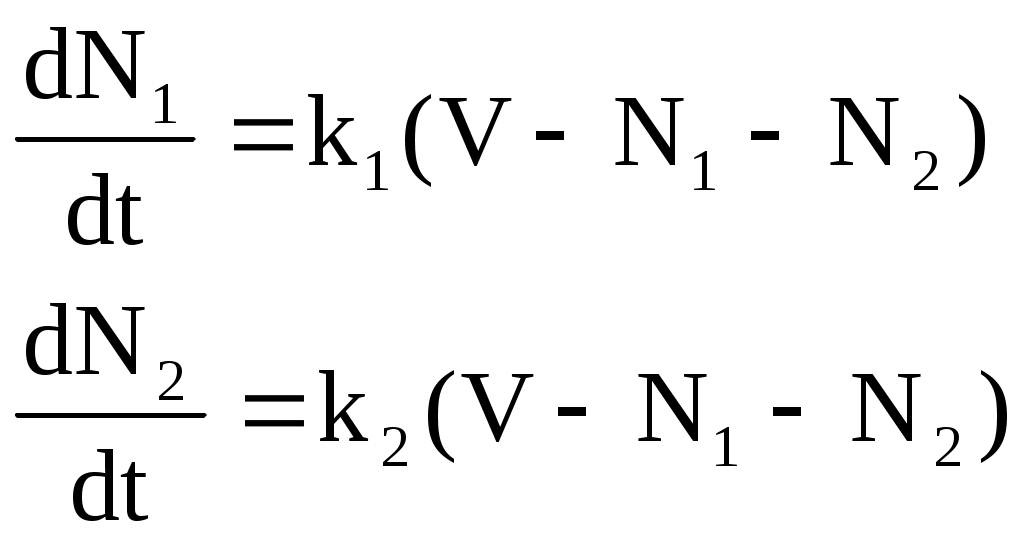
где k₁ и k₂ – некоторые коэффициенты, характеризующие мобильность производства каждой фирмы;

N₁ и N₂ – текущие объемы производства изделия первой и второй фирмами;

V – общий спрос на изделие.

Получить зависимости объема выпуска каждой фирмы от времени при различных начальных объемах выпуска и коэффициентах мобильности.

3. 
   Сезонное производство
   

Спрос на многие изделия носит сезонный характер. Пусть, к примеру, его зависимость от времени описывается следующей функцией:

.
Тогда динамика производства этих изделий, подстраиваясь под спрос, будет иметь вид:

.

или

,

где N – текущий уровень производства;

S – общий спрос на изделия в данный момент;

k₁ и k₂ – некоторые коэффициенты.

Указания

а) Входящее в итоговое уравнение время в программе обозначено как переменная с именем tt;

б) Выражаемую уравнением (*) зависимость спроса от времени рассчитать в отдельном столбце;

в) Построить на одном рисунке зависимости S(t) и N(t).

4. 
   Дилеры
   

Проследим динамику развития дилерской сети. Молодые и энергичные дилеры пытаются увеличить спрос на свои товары. Пусть их начальная численность равна D₀. Имеется также N₀ потенциальных покупателей, которым товар будет продан с какой-то вероятностью. Естественно предположить, что с увеличением количества проданного товара, количество желающих заниматься подобной деятельностью возрастает. В то же время это занятие достаточно хлопотное и постепенно дилеры переходят к другим видам деятельности. Т. е. их численность вследствие естественных причин постоянно уменьшается.

Если провести аналогичные рассуждения относительно покупателей, то нетрудно прийти к модели типа «хищник – жертва». При этом дилеры – это «хищники», а покупатели – «жертвы» (если почитать современную прессу, то аналогия полная – к примеру, когда старушкам продают совершенно ненужный им, а иногда и не работающий, очередной китайский прибор «от всех болезней»).

Данная модель описывается системой:

---

,

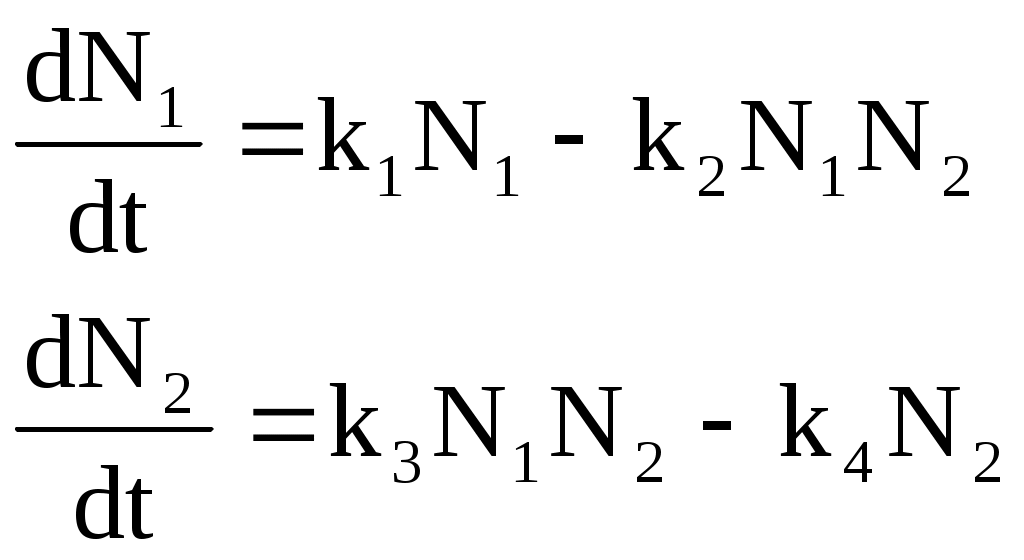где N₁ и N₂ – текущие количества жертв и хищников;

k₁, k₂, k₃, k₄ – соответственно коэффициент размножения жертв, вероятность быть съеденным при встрече с хищником (для жертв), вероятность поймать жертву (для хищников), коэффициент смертности (для хищников).

5. 
   Рыночные отношения
   

При невысоких ценах на некоторые товары (например, на землю) появляется и соответствующий спрос. Но тогда повышение спроса провоцирует повышение цены на этот товар. В результате повышения цен спрос начинает падать. Следствием этого является падение цен. И т. д. Динамику такого взаимодействия можно описать следующим образом:

,

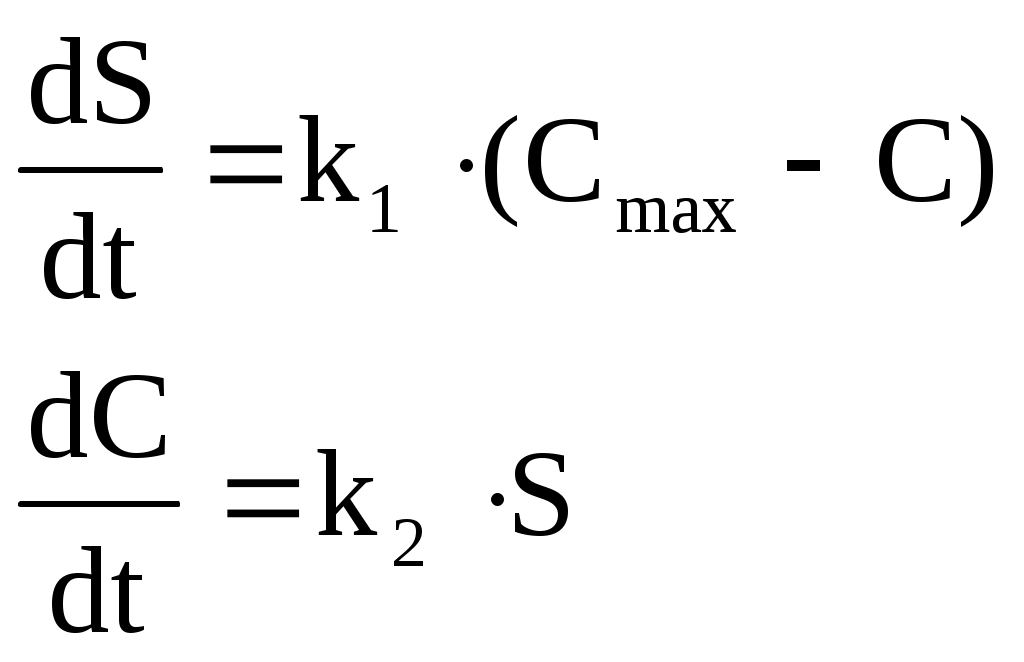где C – цена;

C_max – максимально возможная цена, при которой спрос обращается в нуль;

S – спрос;

k₁ и k₂ – некоторые коэффициенты.

Проследить поведение системы при различных начальных значениях цены и спроса.

Указание

При вводе уравнения в программу вместо C_max следует указывать конкретное число.

6. 
   Взаимопоставки
   

Современное производство основано на специализации. При этом обычно выстраивается цепочка поставок продукции от одних предприятий другим. Например, одно предприятие выпускает полупроводниковые детали, второе – собирает из них приборы, а третье – использует эти приборы в своих машинах. Динамику производства всех трех предприятий можно описать системой уравнений:

,

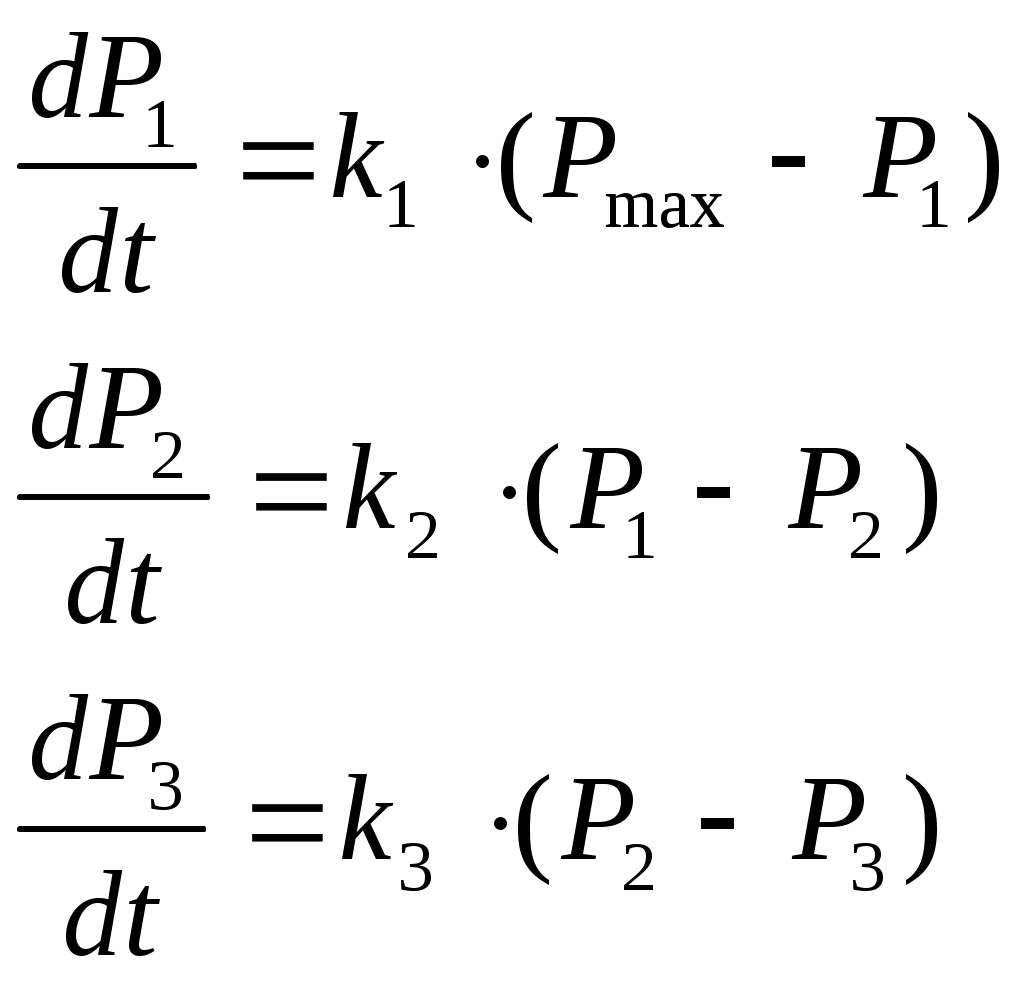где P_max – максимальная потребность в изделиях третьего предприятия.;

P₁, P₂, P₃ – текущие объемы выпуска предприятий;

k₁, k₂, k₃ – коэффициенты мобильности производств на соответствующих предприятиях.

Указание

При вводе уравнения в программу вместо P_max следует указывать конкретное число.

7. 
   Цены в условиях ограниченного объема выпуска
   

Предположим, что имеется изделие с ограниченным выпуском. Пусть это будет редкое лекарство, для которого сырье в очень небольших количествах завозится из джунглей Амазонки. При повышении спроса на это лекарство имеет смысл поднять цены на него. Но с повышением цены начнет падать и спрос. В конце концов,

---

должна установиться такая цена, при которой спрос равен производству. Динамику такого процесса можно описать следующей системой уравнений:
,
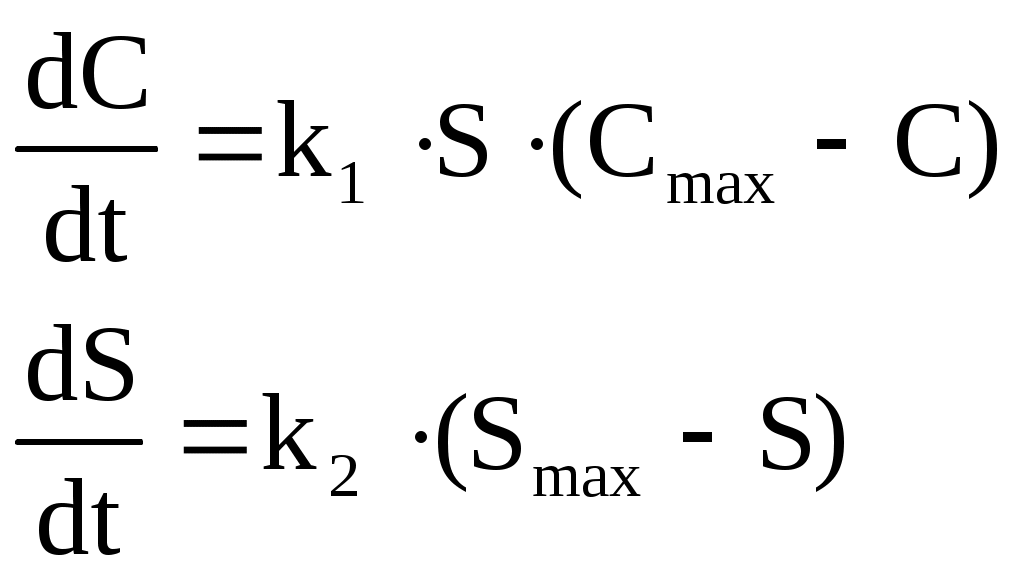где C и S – текущие значения цены и спроса;

C_max – максимальная цена, которую могут заплатить покупатели за данный товар. Если товар будет дороже, то покупатели просто переключаться на другой товар;

S_max – максимальное количество выпускаемого товара;

k₁, k₂ – коэффициенты пропорциональности.

Указание

При вводе уравнений в программу вместо C_max и S_max следует указывать конкретное число.

8. 
   Северный завоз
   

На короткое полярное лето для навигации открываются реки, по которым в полярные города завозятся товары (продовольствие, горючее и т. д.). До начала навигации все товары, предназначенные к отправке, скапливаются на складах. К моменту открытия навигации известно начальное количество товаров. При открытии навигации начинается перегрузка товара на речной транспорт, затем следует перевозка и разгрузка в пункте назначения.

Таким образом, а процессе завоза товар находится в трех состояниях: на исходных складах, на транспорте и на конечных складах. Динамика процесса перевозки описывается системой уравнений:

,
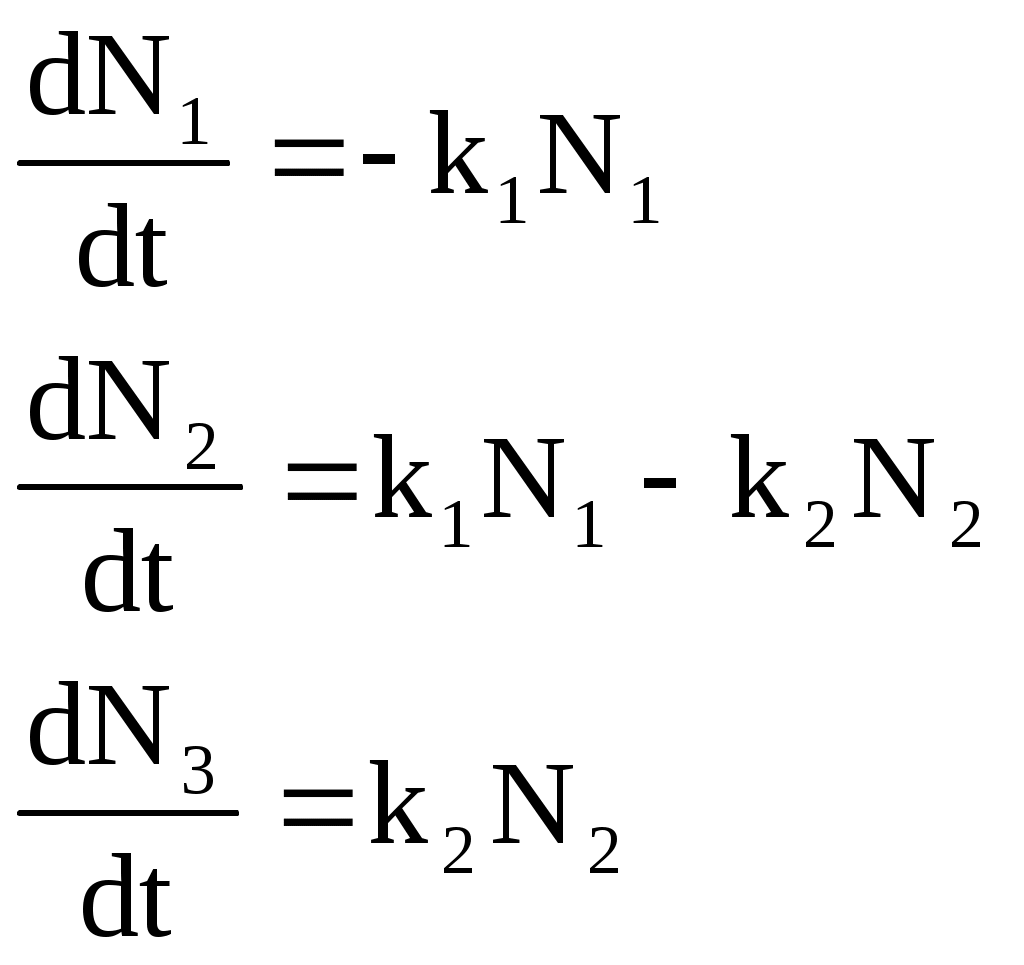где N₁, N₂, N₃ – количество товаров, находящихся соответственно на исходных складах, в процессе транспортировки и на конечных складах;

k₁, k₂ – коэффициенты, характеризующие скорость погрузки и выгрузки товаров.

9. 
   Два пароходства
   

Для реализации северного завоза были заключены контракты с двумя пароходствами. Транспортная мощность первого составляет k₁, а второго – k₂. Динамика перевозки описывается следующей системой уравнений:
,
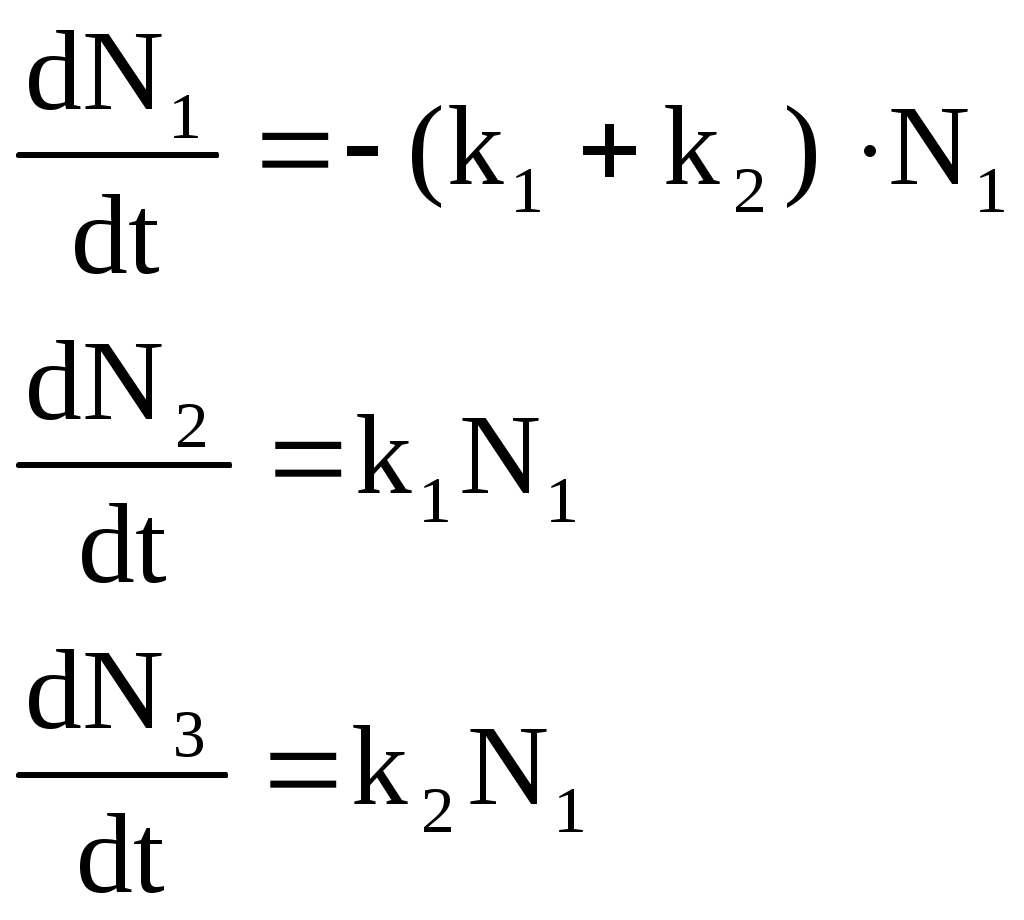где N₁ – общее количество грузов;

N₂ – количество грузов, перевезенных первым пароходством;

N₃ – количество грузов, перевезенных вторым пароходством.

10. 
    Последовательные перевозки
    

Для реализации того же северного завоза может использоваться схема последовательных перевозок. При этом исходные груза сначала скапливаются на складах железной дороги. При открытии северных рек для навигации, накопленные товары грузятся в железнодорожные составы и перевозятся на склады речных пароходств. С этих складов уже пароходами грузы перевозятся на конечные склады. Динамика перемещения грузов описывается следующим образом:

---