Файл: Контрольная работа по теме Базы данных в Excel 72 IV. Макросы в ms excel 78 Макросы для автоматизации работ 78.doc

,

где N₁, N₂, N₃ – количество товаров, находящихся соответственно на исходных складах, на складах пароходства и на конечных складах;

k₁, k₂ – коэффициенты, характеризующие скорость погрузки и выгрузки товаров.

11. 
    Антимонопольная система
    

Во многих странах действует антимонопольное законодательство, которое препятствует захвату рынка одним производителем. Одним из мероприятий, препятствующих монополизации, является установка предельных квот монополизации. Типичным примером действенности этого законодательства являются регулярные многомиллионные штрафы, накладываемые на фирму MicroSoft. Динамика этого процесса описывается следующим образом:
,

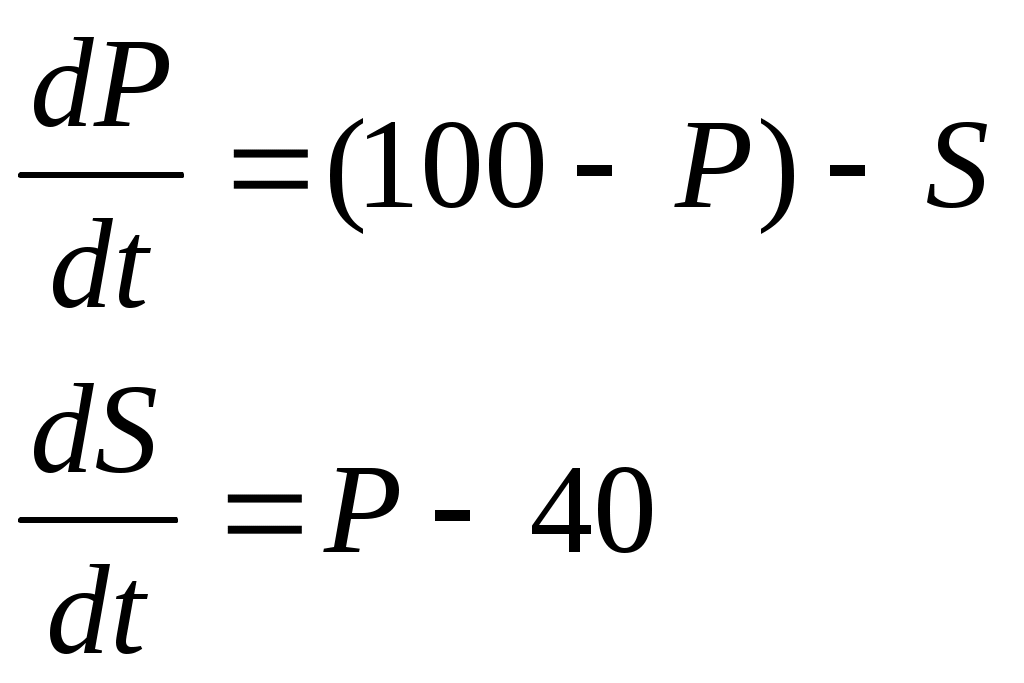где P – объем производства фирмой монополистом (%);

S – сумма штрафов, накладываемых на эту фирму;

100 – весь объем рынка, равный 100%;

40 – максимальная квота захвата рынка, равная 40%.

12. 
    Конъюнктура
    

Имеется ряд товаров не первой необходимости, потребность в которых появляется по конъюнктурным причинам. Это может быть мода на меха, золото, мода на авангардные постановки и т. д.

Динамика такого процесса описывается следующей системой уравнений:
,
где N₁ – число людей, еще не успевших одеться в меха;

N₂ – число людей, щеголяющих в меховых манто;

N₃ – число людей, которым эта мода уже надоела;

k₁, k₂ – некоторые коэффициенты.

13. 
    Количество информации в Интернет
    

В настоящее время наблюдается рост как самой сети Интернет, так и количества хранящейся в ней информации. На сегодняшний момент времени динамику процесса можно описать следующим уравнением:
,
Где I – количество информации;

k, n – некоторые коэффициенты.

---

14. 
    Валютная интервенция
    

В преддверии выборов президент дал указание директору Центробанка произвести мероприятия по сдерживанию курса доллара. У директора для этого есть только одна возможность – интервенция валютных резервов. Поскольку запасы валюты ограничены, спрашивается, сколько времени удастся сдерживать курс доллара, если известны величина валютных резервов и темп инфляции.

Динамика этого процесса описывается следующим образом:
,

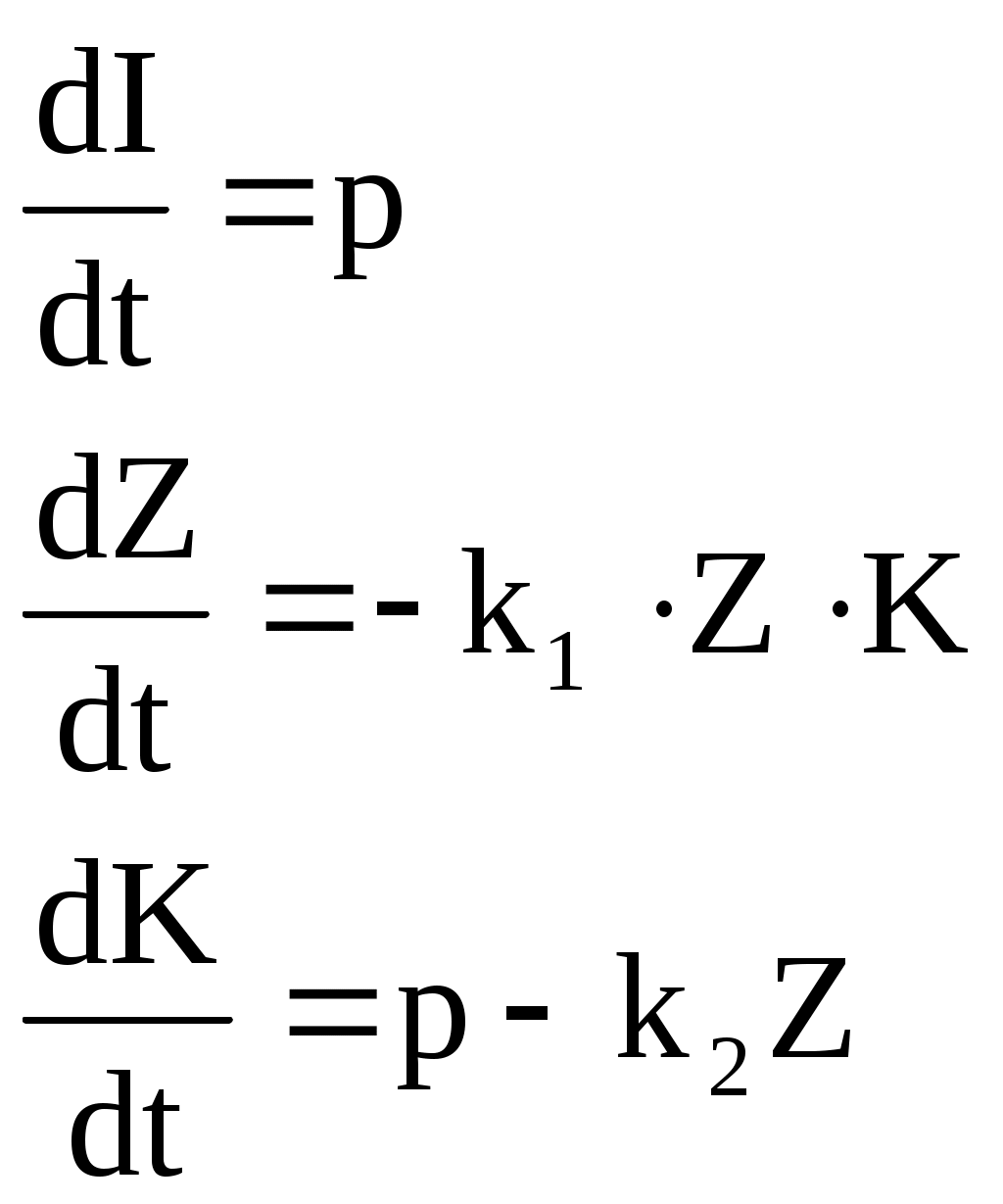где p – темп инфляции;

I – величина инфляции;

K – текущие запасы валюты;

k₁, k₂ – некоторые коэффициенты.

---

VII. Статистические методы

7.1. Определение характеристик случайных величин

7.1.1. Содержание работы

а) Используя встроенные в Excel функции для представленных наборов данных рассчитать следующие числовые характеристики.
Вычисляемый параметр Функция в Excel

• 
  среднее; СРЗНАЧ
  
• 
  минимальное значение; МИН
  
• 
  максимальное значение; МАКС
  
• 
  размах; МАКС – МИН
  
• 
  медиану; МЕДИАНА
  
• 
  моду; МОДА
  
• 
  дисперсию; ДИСПА
  
• 
  стандартное отклонение; СТАНДОТКЛОН
  
• 
  вариацию; СТАНДОТКЛОН/ СРЗНАЧ
  
• 
  коэффициент асимметрии; СКОС
  
• 
  коэффициент эксцесса; ЭКСЦЕСС
  
• 
  95%-ый доверительный интервал. ДОВЕРИТ
  

б) С надежностью 95% выявить промахи.

Промахом называется значение случайной величины в наборе данных, резко отличающееся от остальных. Например:
31, 28, 34, 2, 29, 30.
Очевидно, подчеркнутое значение резко отличается от остальных и является промахом. Их появление в наборах обрабатываемых данных может быть следствием как элементарной опечатки, так и вызвано более глубокими причинами, связанными со свойствами изучаемых объектов.

Для объективного определения является ли какое-либо значение промахом поступают следующим образом:

Вычисляется величина:
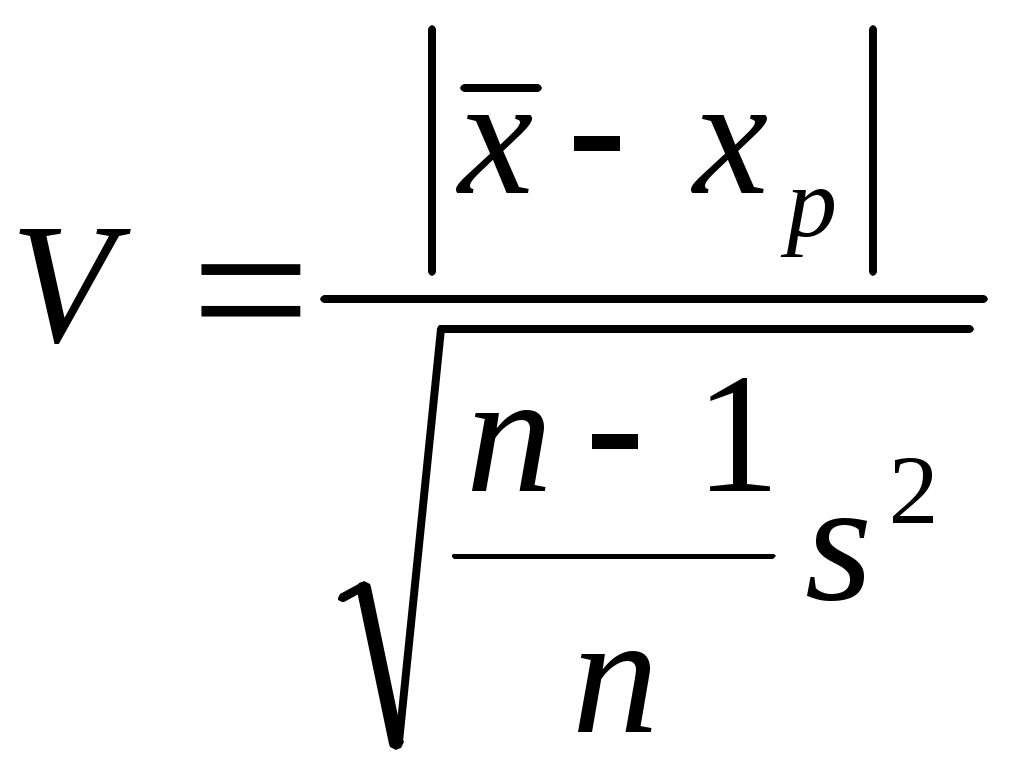, (7.1)

где n – число измерений;

– проверяемое значение;

– среднее значение;

– выборочная дисперсия.

Среднее значение и дисперсия вычисляются с учетом проверяемого значения.

Значения V-критерия приведены в табл. 7.1

Таблица 7.1

Число измерений, N	Уровень значимости
	0,1	0,05	0,01
3	1,41	1,41	1,41
4	1,64	1,69	1,72
5	1,79	1,87	1,96
6	1,89	2,00	2,13
7	1,97	2,09	2,26
8	2,04	2,17	2,37
9	2,10	2,24	2,46
10	2,15	2,29	2,54

---

Если рассчитанное значение больше критического, то проверяемое значение действительно является промахом, и значения дисперсии и среднего следует пересчитать, исключив промах.

В противном случае нет оснований считать измерение промахом.
в) С надежностью 95% выяснить, различны ли дисперсии для различных наборов данных.

Дисперсии сравниваются по критерию Фишера, рассчитываемому по формуле:

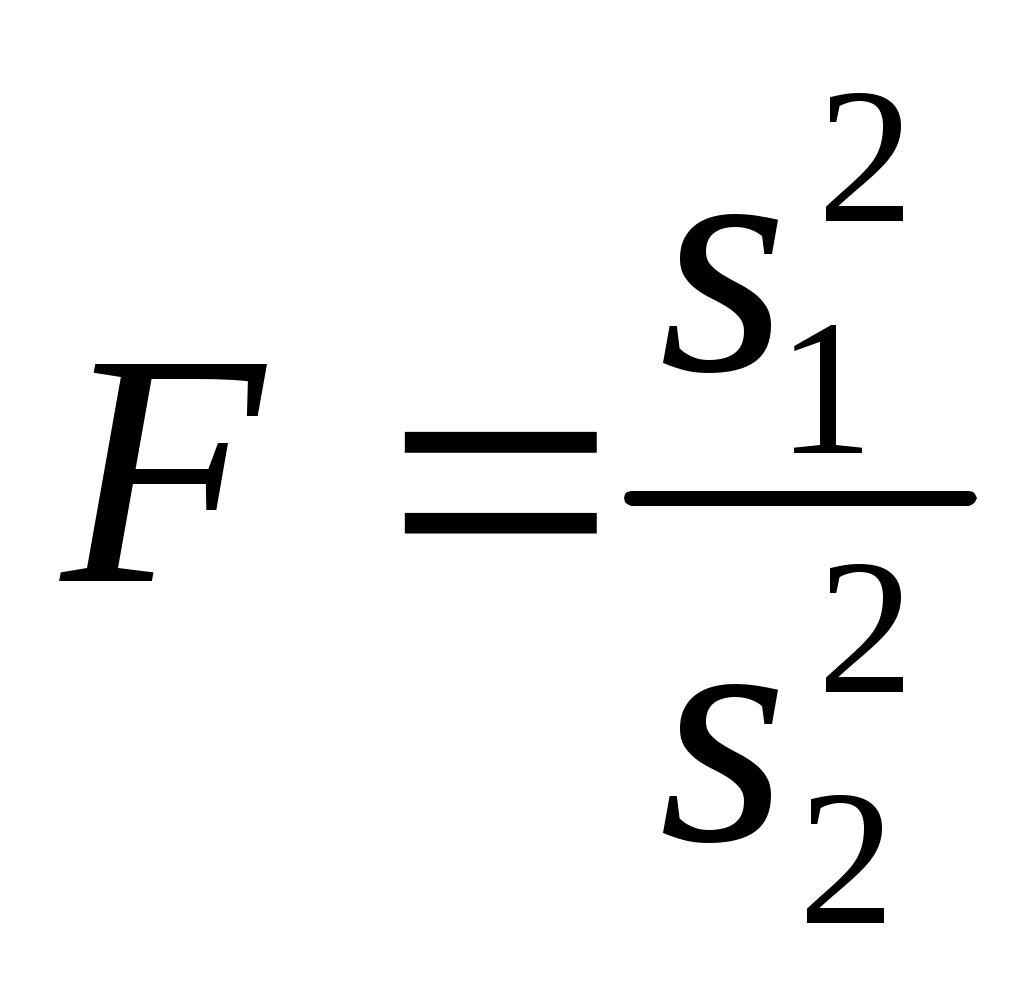, (7.2)
где s₁² – большая дисперсия;

s₂² – меньшая дисперсия.

Если рассчитанное значение F больше критического при выбранной степени риска, то дисперсии считаются статистически различными. Иначе значения дисперсий считаются одинаковыми. Для нахождения критических значений критерия используется функция FРАСПОБР.

Если данные представлены в различных единицах измерения, то вместо дисперсий сравниваются вариации. При этом критерий Фишера рассчитывается по формуле:

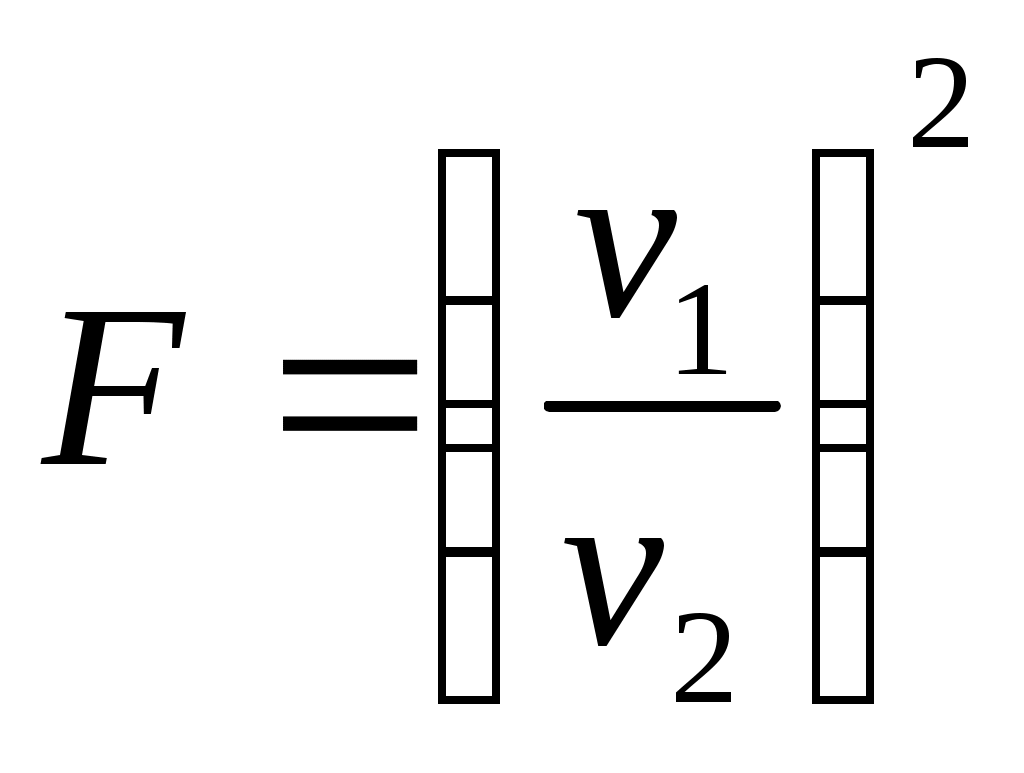, (7.3)
где v₁ – большая вариация;

v₂ – меньшая вариация.
7.1.2. Варианты заданий

Номер варианта соответствует номеру студента по журналу группы.
Вариант 1

Валовая продукция некоторых предприятий ЧАССР за 1932-1933 года
Наименование предприятия	Валовая продукция в неизменных ценах	Число рабочих
Козловский комбинат.	6449	1555
Вурнарский комбинат	202,6	78
Чебоксарский кирпичный завод	55,9	44
Шумерлинский комбинат	2271,9	580
Ядринский маслобойный завод	731,1	68
Сюктерский лесозавод	865,7	152

---

Вариант 2

Посевные площади и сбор волокна льна в 1913 году в 6 льноводческих губерниях России
Губернии	Посевная площадь, дес	Общий сбор, тыс.пуд
Вологодская	26976	736,3
Ковенская	42124	1375,6
Московская	20025	550,7
Новгородская	27647	799
Томская	40728	1247,7
Ярославская	37371	1091,2

Вариант 3

Убыль населения за 1914-1918
Страны	Потери людей, млн. человек	Понижение рождаемости, млн.человек
Франция	1,4	2
Англия	0,7	1
Германия	2	4,2
Австро-венгрия	1,4	4,4
Италия	0,5	1,6
США	0,08	0,32

Вариант 4

Увеличение в центральном нечерноземном районе пашни за счет вырубки лесов
годы	Пашня (млн. дес)	Лес (вырубка)
1696	21	47
1711	23	49
1725	25	51
1742	27	54
1763	30	56

---