Файл: 1 Теоретические сведения Свойства и назначение нейронных сетей.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 8
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Аппроксимация функций с помощью нейронных сетей
Цель работы: изучение принципов функционирования нейронных сетей (НС) в рабочем режиме и режиме обучения.
1 Теоретические сведения
-
Свойства и назначение нейронных сетей
Под методами искусственного интеллекта понимают все методы и математические модели, которые имитируют мыслительную (интеллектуальную) деятельность человека. В этом отношении можно выделить два подхода:
– моделирование процесса (алгоритма) мышления при принятии какого-либо решения,
– моделирование работы мозга на основе изучения биологических принципов его функционирования.
Первый подход реализуется в виде нечетких логических функций (Fuzzy Logic), экспертных систем, естественно-языковых систем. Второй подход представлен нейронными сетями, которые фактически являются математическими моделями мозга.
Основные свойства НС:
– массивно-параллельная обработка,
– высокая отказоустойчивость,
– использование неалгоритмических вычислений,
– способность к обобщению и классификации данных,
– способность к обучению с учителем или без учителя,
– возможность использования слабоформализованной информации.
НС получили распространение благодаря тому, что они:
– дают стандартный способ решения многих нестандартных задач;
– обладают способностью к обучению – необходимо только формировать учебные задачники, то есть труд программиста замещается трудом учителя;
– особенно эффективны там, где нужен аналог человеческой интуиции;
– позволяют создавать эффективное программное обеспечение для компьютеров с высокой степенью параллельной обработки.
В литературе встречается значительное число признаков, которыми должна обладать задача, чтобы применение НС было оправдано и НС могла бы ее решить:
– отсутствует алгоритм или не известны принципы решения задач, но накоплено достаточное число примеров
;
– проблема характеризуется большими объемами входной информации;
– данные неполны или избыточны, зашумлены, частично противоречивы.
Таким образом, НС хорошо подходят для распознавания образов и решения задач классификации, оптимизации и прогнозирования. В нефтяной и химической промышленности НС могут применяться для анализа геологической информации, идентификация неисправностей оборудования, разведки залежей минералов по данным аэрофотосъемок, анализа составов примесей, при управлении процессами. Кроме того, с помощью НС может быть реализовано управление манипуляторами, управление качеством, обнаружение неисправностей, адаптивная робототехника, управление голосом и т.д.
2 Практическая часть
Создадим обобщенно-регрессионную НС с именем а для аппроксимации функции вида у=4cos(x)/x на отрезке [1;5], используя следующие экспериментальные данные:
х = [1 1.4 1.8 2.2 2.6 3 3.4 3.8 4.2 4.6 5].
y = [2.16 0.49 -0.5 -1.07 -1.318 -1.32 -1.14 -0.83 -0.47 -0.1 0.23].
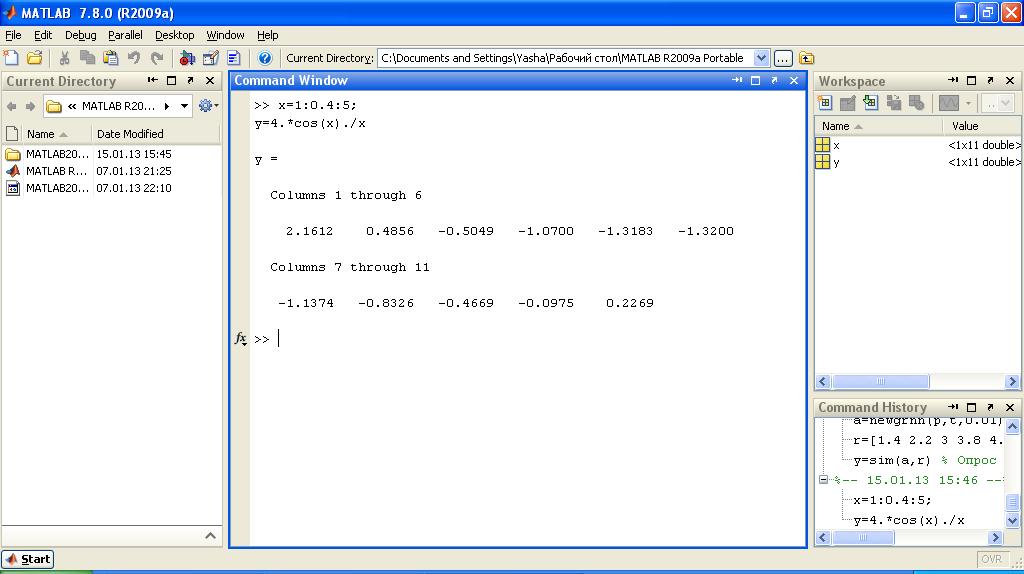
Рисунок 1 – Расчет значений функции вручную
Процедура создания и использования данной НС описывается следующим образом:
% Задание входных значений
p=[1 1.4 1.8 2.2 2.6 3 3.4 3.8 4.2 4.6 5];
% Задание выходных значений
t=[2.16 0.49 -0.5 -1.07 -1.318 -1.32 -1.14 -0.83 -0.47 -0.1 0.23];
a=newgrnn(p,t,0.01); % Создание НС с отклонением 0.01
r=[1.4 2.2 3 3.8 4.6];
y=sim(a,r) % Опрос НС
y= 0.4900 -1.0700 -1.3200 -0.8300 -0.1000
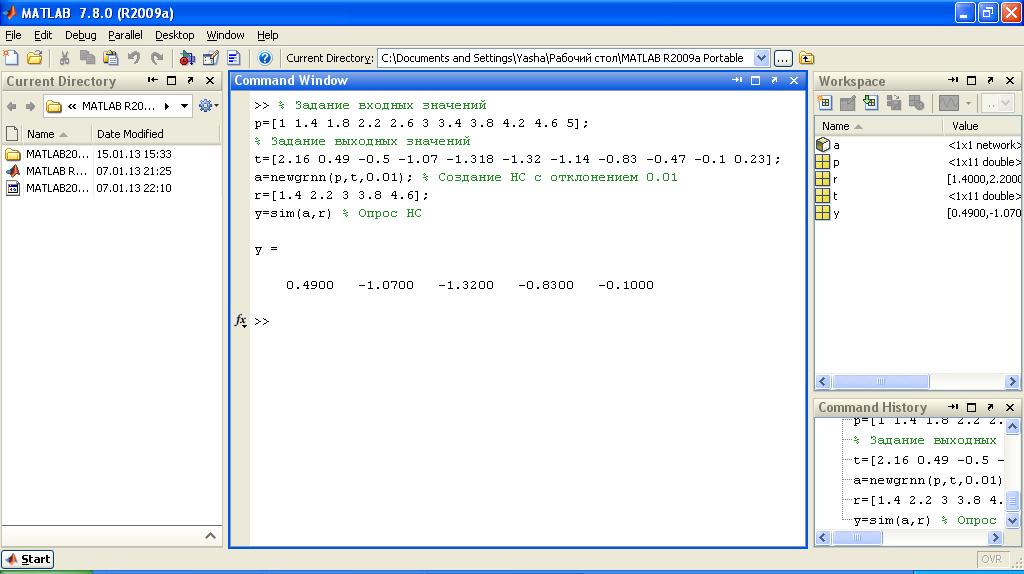
Рисунок 2 – Моделирование нейронной сети
Точность аппроксимации в данном случае высокая.
Проведем обучение нейронной сети
% Задание входных значений
p=[1 1.4 1.8 2.2 2.6 3 3.4 3.8 4.2 4.6 5];
% Задание выходных значений
t=[2.16 0.49 -0.5 -1.07 -1.318 -1.32 -1.14 -0.83 -0.47 -0.1 0.23];
net=newff([1 5],[5 1],{'tansig' 'purelin'});
net.trainParam.epochs=100; % Задание числа эпох обучения
net=train(net,p,t); % Обучение сети
z=sim(net,p); % Опрос обученной сети
figure(1);
hold on;
hold on;
xlabel('p');
ylabel('t');
plot(p,t,p,z,'o'), grid; % Прорисовка графика исходных данных и функции,
сформированной нейронной сетью
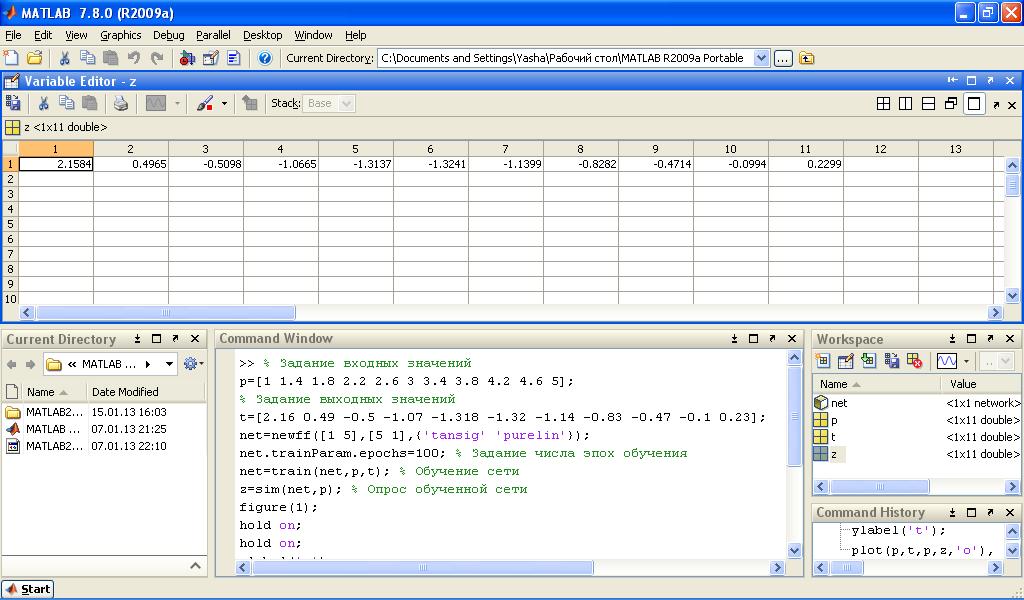
Рисунок 3 – Выходные значения обученной НС
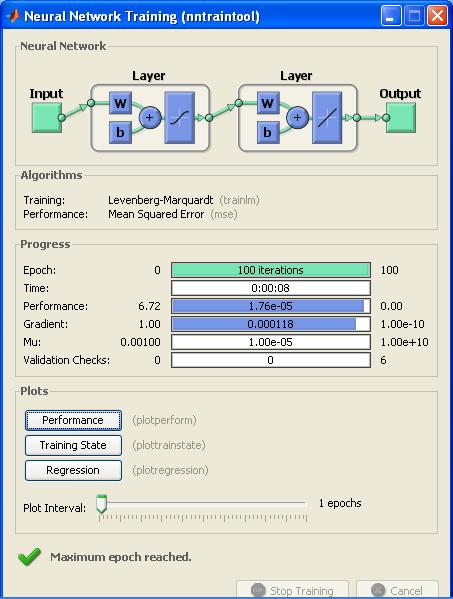
Рисунок 4 – Процесс обучения НС
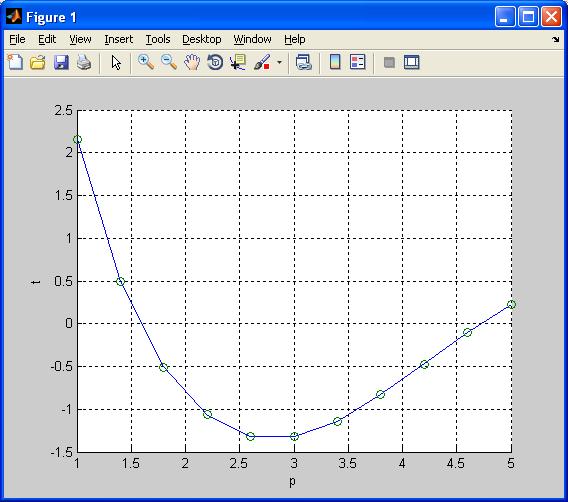
Рисунок 5 – График полученной функции
Вывод: в ходе лабораторной работы я изучил принципы функционирования нейронных сетей (НС) в рабочем режиме и режиме обучения.