Файл: Федеральное государственное общеобразовательное учреждение высшего образования.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 33
Скачиваний: 30
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| | |
Федеральное государственное общеобразовательное учреждение высшего образования
<<Чувашский государственный университет имени И.Н. Ульянова>>
Кафедра промышленной электроники
Расчетно-графическая работа
по дисциплине:
<<Теоретические основы цифровой электроники>>
Вариант: №10
Выполнил:
Студент группы: РЭА-31-20
Егоров Юрий Владиславович
Проверил:
Григорьев В.Г.
Чебоксары 2021
Содержание
Задание 1……………………………………………………………...3
Задание 4……………………………………………………………...3
Задание 5……………………………………………………………...5
Задание 6……………………………………………………………...5
Задание 9……………………………………………………………...5
Задание 10…………………………………………………………….8
Задание 12…………………………………………………………….9
Задание 13…………………………………………………………….10
Задание 14…………………………………………………………….10
Задание 16…………………………………………………………….11
Список использованной литературы……………………………….13
Задание 1.
Докажите тождества, используя только определения операций над множествами.
1)
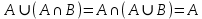
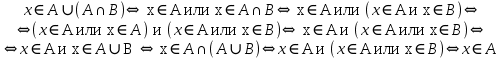
2)
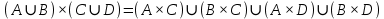
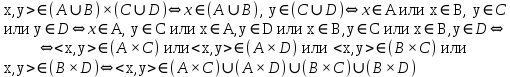

 Задание 4.
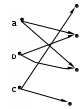
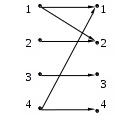
Задание 4. A={a,b,c}, B={1,2,3,4},
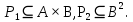 Изобразите
Изобразите 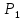 ,
, 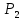 графически. Найдите [
графически. Найдите [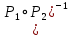 ]. Проверьте с помощью матрицы [
]. Проверьте с помощью матрицы [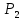 ], является ли отношение
], является ли отношение 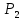
рефлексивным, симметричным, антисимметричным, транзитивным?
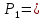





1
2
3
4
[
 ]=
]=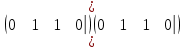 [
[ ]=
]=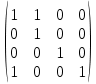
[
 ]=
]=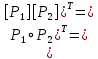


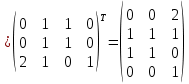
1) [
 ]=
]=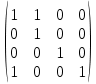 – по диагонали нет нулей
– по диагонали нет нулей 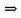
 – рефлексивно.
– рефлексивно.2)
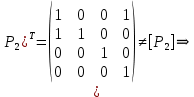
 – несимметрично.
– несимметрично.3)
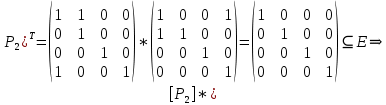
 – антисимметрично.
– антисимметрично.4)
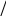
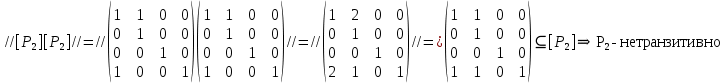



Задание 5.
Найдите область определения
, область значений отношения P. Является ли отношение P рефлексивным, симметричным, антисимметричным, транзитивным?
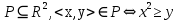
Область определения:
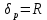
Область значений:
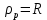
 1)
1) 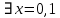 :
: 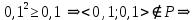 P – нерефлексивно.
P – нерефлексивно.2) Так как
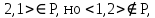 то P – несимметрично
то P – несимметрично3) Так как
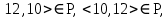 но
но 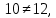 поэтому P – неантисимметрично.
поэтому P – неантисимметрично.4) Так как
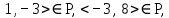 при этом,
при этом, 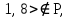 поэтому P нетранзитивно.
поэтому P нетранзитивно.

Задание 6.
Является ли алгеброй следующий набор B=
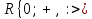 ?
?Так как
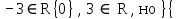 при подстановке в термы, получаем
при подстановке в термы, получаем 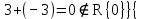 , то есть операция сложения не замкнута на множестве R\{0}, поэтому набор не является алгеброй.
, то есть операция сложения не замкнута на множестве R\{0}, поэтому набор не является алгеброй.

Задание 9.
Даны графы
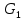 и
и 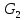 . Найдите
. Найдите 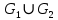 ,
, 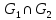 ,
, 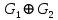 ,
, 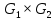 . Для графа
. Для графа 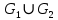 найдите матрицы смежности, инцидентности, сильных компонент, маршрутов длины 2 и все маршруты длины 2, исходящие из вершины 1.
найдите матрицы смежности, инцидентности, сильных компонент, маршрутов длины 2 и все маршруты длины 2, исходящие из вершины 1.
















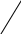







3
2
1
4
3
2
1
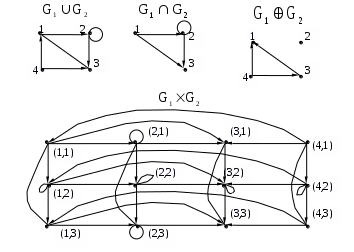
Рассмотрим граф
 :
:Матрица смежности A=
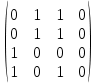
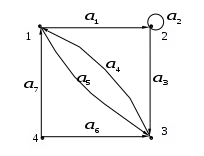
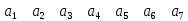
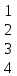
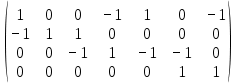 – матрица инцидентности
– матрица инцидентности B=E+A+
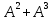 =
=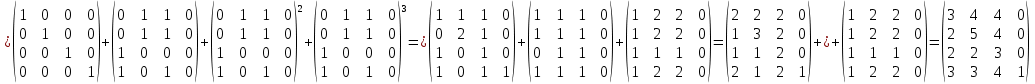
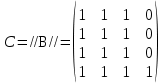
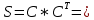
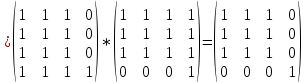 – матрица сильных компонент.
– матрица сильных компонент.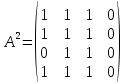 – матрица маршрутов длины 2.
– матрица маршрутов длины 2.Маршруты длины 2, исходящие из вершины 1:
(1;3;1), (1;3;2), (1;2;3).


Задание 10.
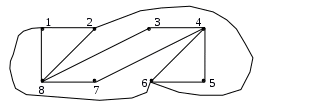
Найдите матрицы фундаментальных циклов, фундаментальных разрезов, радиус и диаметр, минимальное множество покрывающих цепей графа G. Является ли изображенный граф эйлеровым? Является ли изображенный граф планарным?

3


2
4
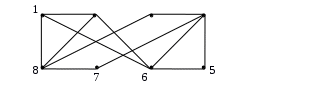
Получим остов графа. Для этого удалим из графа 12–8+1=5 ребер.

3
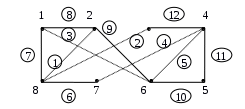
Матрица фундаментальных циклов:
C=
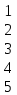
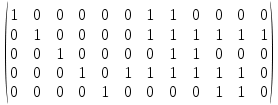
Матрица фундаментальных разрезов:
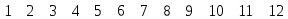
K=
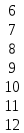
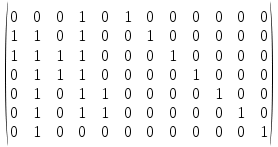
Диаметр d(G)=3
Радиус r(G)=2
Минимальное множество покрывающих цепей графа – 1.
1,6,5,4,3,8,2,1,8,7,4,6,2
Граф не является эйлеровым, так как степени не всех его вершин четные.
Граф планарный.
Задание 12.
Проверьте двумя способами, будут ли эквивалентны следующие формулы