Файл: Федеральное государственное общеобразовательное учреждение высшего образования.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 34
Скачиваний: 30
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
=x (y
(y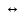 z) и
z) и 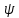 =(x
=(x y)
y)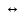 (x
(x z)
z)
а) составлением таблиц истинности
б) приведением формул к СДНФ или СКНФ с помощью эквивалентных преобразований.
а)
Так как столбцы и
и  совпадают, то формулы эквивалентны.
совпадают, то формулы эквивалентны.
б)
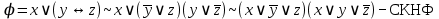
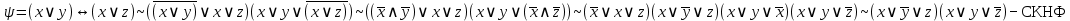 Так как СКНФ совпадают, то формулы эквивалентны.
Так как СКНФ совпадают, то формулы эквивалентны.


Задание 13.
С помощью эквивалентных преобразований приведите формулу к ДНФ, КНФ, СДНФ, СКНФ. Постройте полином Жегалкина.
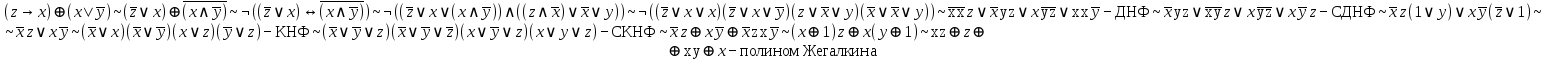


Задание 14.
Найдите сокращенную, все тупиковые и минимальные ДНФ булевой функции двумя способами:
двумя способами:
а) методом Квайна б) с помощью карт Карно
Каким классам Поста принадлежит эта функция?
а)

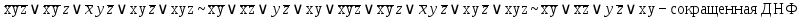
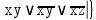 тупиковые и минимальные ДНФ.
тупиковые и минимальные ДНФ.
б)
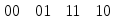
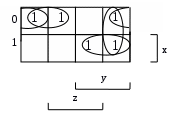
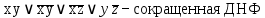
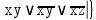 тупиковые и минимальные ДНФ.
тупиковые и минимальные ДНФ.
1)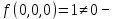 функция не сохраняет ноль
функция не сохраняет ноль
2)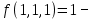 функция сохраняет единицу
функция сохраняет единицу
3)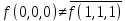 – функция несамодвойственная.
– функция несамодвойственная.
 4)
4) 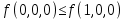 – функция немонотонная
– функция немонотонная
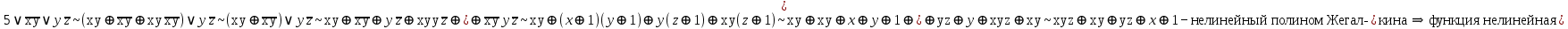


Задание 16.
Является ли полной система функций J=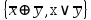 ? Образует ли она базис?
? Образует ли она базис?
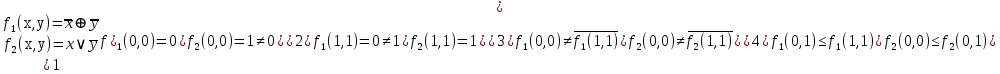
функция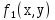 сохраняет ноль
сохраняет ноль
функция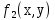 не сохраняет ноль
не сохраняет ноль
функция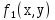 не сохраняет единицу
не сохраняет единицу
функция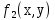 сохраняет единицу
сохраняет единицу
функция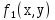 несамодвойственная
несамодвойственная
функция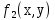 несамодвойственная
несамодвойственная
функция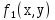 немонотонная
немонотонная
функция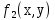 немонотонная
немонотонная
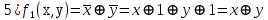
функция линейная, т. к. полином Жегалкина линейный
линейная, т. к. полином Жегалкина линейный
Так как для каждого из классов в системе Jнайдется функция, не принадлежащая этому классу, то система булевых функций J полная. Удаление любой из функций приведет к тому, что система станет неполной. Значит, она образует базис.


Список использованной литературы
Учебник С.В. Судоплатов, Е.В. Овчинникова Элементы дискретной метематики

 (y
(y z) и
z) и  =(x
=(x y)
y)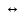 (x
(x z)
z)а) составлением таблиц истинности
б) приведением формул к СДНФ или СКНФ с помощью эквивалентных преобразований.
а)
| x | y | z | y 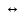 z z |  | x  y y | x  z z | 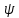 |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Так как столбцы
 и
и  совпадают, то формулы эквивалентны.
совпадают, то формулы эквивалентны.б)
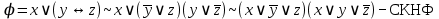
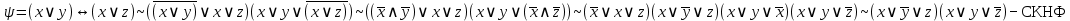 Так как СКНФ совпадают, то формулы эквивалентны.
Так как СКНФ совпадают, то формулы эквивалентны.

Задание 13.
С помощью эквивалентных преобразований приведите формулу к ДНФ, КНФ, СДНФ, СКНФ. Постройте полином Жегалкина.
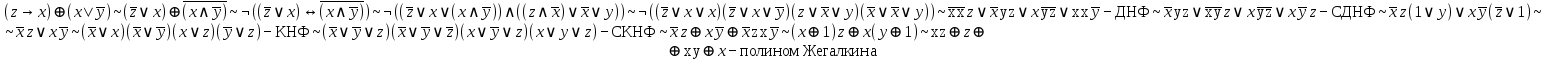


Задание 14.
Найдите сокращенную, все тупиковые и минимальные ДНФ булевой функции
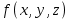 двумя способами:
двумя способами:а) методом Квайна б) с помощью карт Карно
Каким классам Поста принадлежит эта функция?
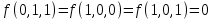
а)

| x | y | z | 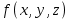 |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
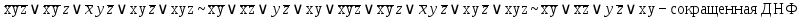
| |  |  | 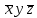 | 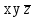 | 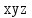 |
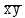 | * | * | | | |
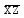 | * | | * | | |
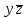 | | | * | * | |
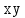 | | | | * | * |
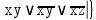 тупиковые и минимальные ДНФ.
тупиковые и минимальные ДНФ. б)
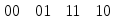

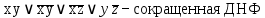
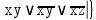 тупиковые и минимальные ДНФ.
тупиковые и минимальные ДНФ. 1)
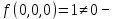 функция не сохраняет ноль
функция не сохраняет ноль2)
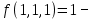 функция сохраняет единицу
функция сохраняет единицу3)
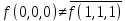 – функция несамодвойственная.
– функция несамодвойственная.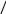 4)
4) 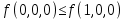 – функция немонотонная
– функция немонотонная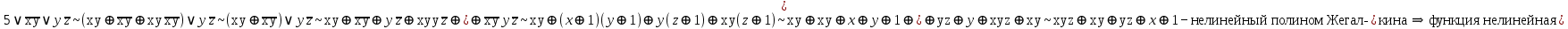


Задание 16.
Является ли полной система функций J=
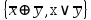 ? Образует ли она базис?
? Образует ли она базис?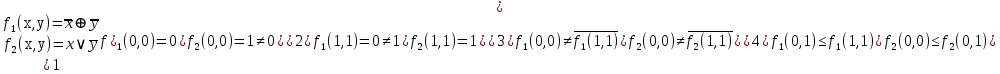
функция
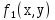 сохраняет ноль
сохраняет нольфункция
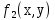 не сохраняет ноль
не сохраняет нольфункция
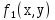 не сохраняет единицу
не сохраняет единицуфункция
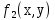 сохраняет единицу
сохраняет единицуфункция
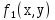 несамодвойственная
несамодвойственнаяфункция
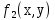 несамодвойственная
несамодвойственная
функция
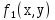 немонотонная
немонотоннаяфункция
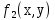 немонотонная
немонотонная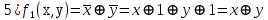
функция
 линейная, т. к. полином Жегалкина линейный
линейная, т. к. полином Жегалкина линейный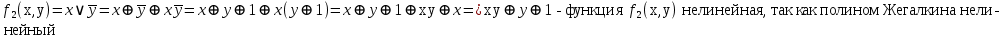
| Функция | Классы | ||||
| P0 | P1 | S | M | L | |
 | да | нет | нет | нет | да |
 | нет | да | нет | нет | нет |
Так как для каждого из классов в системе Jнайдется функция, не принадлежащая этому классу, то система булевых функций J полная. Удаление любой из функций приведет к тому, что система станет неполной. Значит, она образует базис.


Список использованной литературы
Учебник С.В. Судоплатов, Е.В. Овчинникова Элементы дискретной метематики
