Файл: Кинематический анализ зубчатых механизмов.docx

18 ВОПРОСКинематический анализ зубчатых механизмовЦелью кинематического анализа является определение угловых скоростей звеньев и передаточных отношений.Передаточное отношение между звеньями a и b определяется как отношение их угловых скоростей (или частот вращения): . (3.1)Угловые скорости и частоты вращения связаны соотношениями ;  .Очевидно, что перестановка индексов у величины  приводит к получению обратной величины, т.е. .Если оси вращения звеньев a и b параллельны, то передаточному отношению  и угловым скоростям и присваиваются знаки «+» или «-» по следующим правилам: любое из двух возможных направлений вращения принимают за положительное (обычно положительным считают направление вращения входного вала механизма), тогда угловая скорость каждого звена кинематической цепи приобретает вполне определенный знак; при одинаковом направлении угловых скоростей, входящих в (3.1), они имеют одинаковые знаки и, следовательно, определяют положительное передаточное отношение.

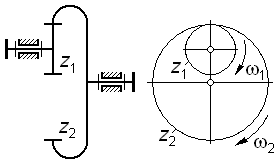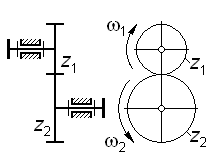Рис. 3.1		Рис. 3.2

---

Очевидно, что для пары внутреннего зацепления (рис. 3.1) передаточное отношение , (3.2)а для пары внешнего зацепления (рис. 3.2) - . (3.3)19 ВОПРОСЦелью кинематического анализа является определение угловых скоростей звеньев и передаточных отношений.Передаточное отношение между звеньями a и b определяется как отношение их угловых скоростей (или частот вращения): . (3.1)Угловые скорости и частоты вращения связаны соотношениями ;  .Очевидно, что перестановка индексов у величины  приводит к получению обратной величины, т.е. .Если оси вращения звеньев a и b параллельны, то передаточному отношению  и угловым скоростям и присваиваются знаки «+» или «-» по следующим правилам: любое из двух возможных направлений вращения принимают за положительное (обычно положительным считают направление вращения входного вала механизма), тогда угловая скорость каждого звена кинематической цепи приобретает вполне определенный знак; при одинаковом направлении угловых скоростей, входящих в (3.1), они имеют одинаковые знаки и, следовательно, определяют положительное передаточное отношение.

Рис. 3.1		Рис. 3.2

---

Очевидно, что для пары внутреннего зацепления (рис. 3.1) передаточное отношение , (3.2)а для пары внешнего зацепления (рис. 3.2) - . (3.3)20 ВОПРОС

Графический метод кинематического анализа зубчатых механизмов

Графический метод применяют для определения линейных скоростей любой точки любого звена механизма, угловых скоростей его звеньев и передаточного отношения механизма.Линейную скорость точки звена, совершающего вращательное движение, определяют: (14)где ω – угловая скорость вращения звена относительно мгно­венного центра вращения;R – расстояние точки до мгновенного центра вращения.Из выражения (14) можно заключить, что при ω=const скорости точек меняются по линейному закону, для построения которого необходимо знать скорости только двух точек.21 ВОПРОС

Эпициклические механизмы и передачи

Они бывают дифференциальными, планетарными и замкнутыми дифференциальными.Устройство этих трех видов передач аналогично: в их состав входят зубчатые колеса с подвижными и неподвижными осями вращения. В осно­ву положен дифференциальный механизм.Дифференциальные зубчатые механизмы. Устройство и кинематикаПусть мы имеем два соосных, независимых друг от друга централь­ных зубчатых колеса z₁и z₂- одно с внешними, другое с внутреннимизубьями (рис. 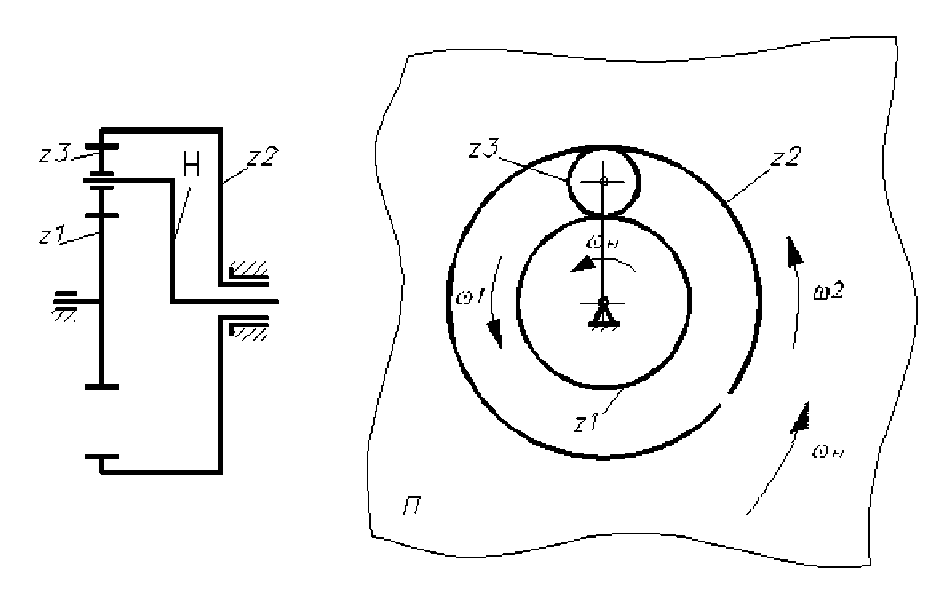5.17).Рис. 5.17. Обращение движения в дифференциальном механизмеТакая механическая система имеет две степени свободы^ = 2). Не­зависимо от положения колес радиальный зазор между их делительными окружностями одинаков. Поэтому в этот зазор можем ввести зубчатое ко­лесо 

---

z₃(сателлит), который не изменит фактическую степень подвижности (W = 2). Сателлит является пассивной связью, т.к. сможет произвольно пе­рекатываться в зазоре, не связывая независимое вращение колес Z₁, Z₂. Са­теллитов, как правило, несколько. Как бы не располагался сателлит, рас­стояние от его центра до оси колес не меняется, поэтому можно ввести ры­чаг - водило Н, снимающий движение с оси сателлита при вращении во­круг оси центральных колес.Полученный механизм по-прежнему обладает двумя степенями сво­боды и является дифференциальным. Он позволяет сложить угловые ско­рости о\, со₂ и получить угловую скорость со_я как результат этого сложе­ния. По принципу суперпозиции:«h = ^щ тщ- + ^w2 "ЦТ)^-, (^5ЛЗ)^U1-H ^U 2-Hгде U⁽-H и U22-⁾_H- передаточные отношения от центральных колес 1 и 2к водилу H при независимом их вращении (одно вращается, другое закреп­лено). Чтобы раскрыть формулу (5.1З), воспользуемся методом обращения движения. Для этого введем в рассмотрение плоскость П, которая враща­ется вокруг оси центральных колес с угловой скоростью cw_H, и поместим на эту плоскость наблюдателя. При неподвижном водиле Н (обращенный механизм) наблюдатель видит дифференциальный механизм таким, у которого оси колес непод­вижны.^ziФормула - формула Виллиса.Дифференциальные механизмы применяют, например, в автомоби­лях, чтобы на повороте колеса могли свободно вращаться одно относи­тельно другого, самопроизвольно распределяя суммарную скорость водила cw_Hв соответствии с (5.1 З).

 Планетарные зубчатые механизмы. Кинематика и синтез

П 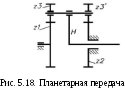ланетарные механизмы получаются из дифференциальных путем закрепления одного из центральных колес. Закрепив, например, колесо 2 (рис. 5.18), в формуле (5.14) имеем со₂ = 0 и тогда с помощью формул (5.13) и (5.14) получим:(5.15)

---