Указания к выполнению контрольной работы №1

Тема 2. Элементы аналитической геометрии на плоскости.

Ефимов, гл 1-3, 4-6

Данко, гл. 1, §1-5.

1. Основные формулы аналитической геометрии.

1 . - длина отрезка между точками и

2. ; - координаты точки деления отрезка в данном отношении.

| | | | |

-отношение величины отрезка от начала отрезка т. M₁ до делящей т. C к величине отрезка от делящей точки C до конца отрезка M₂ .

3. - уравнение прямой линии с угловым коэффициентом.

- угловой коэффициент прямой.

- тангенс угла между двумя прямыми.

-угол между двумя прямыми.

- условие | | двух прямых.

- условие  двух прямых.

y y

b

x x 0 0

рис 1. рис 2.

4. - уравнение пучка прямых.

y

- центр пучка.

M₀

х

0

рис 3.

5. - уравнение прямой, проходящей через две точки и

6. - уравнение прямой, проходящей через точку параллельно вектору +

y

x

0

рис 4.

7. - уравнение прямой, проходящей через т. , перпендикулярно вектору .

y

x

0

М₀

рис. 5

8. - общее уравнение прямой- уравнение первой степени с двумя неизвестными.

9. - уравнение в отрезках на осях.

y

b

0 a x

рис. 6

10. параметрические уравнения прямой.



, t- переменный параметр.

1 1. - уравнение окружности с центром в т. O (0;0) и радиусом r. ( рис. 7 )

---

рис. 7

- уравнение окружности со смещённым центром . (рис. 8)

12. Каноническое уравнение эллипса.

- уравнение эллипса с центром в начале координат.

- уравнение эллипса со смещённым центром в т. O₁(x₀,y₀).

13. Каноническое уравнение гиперболы.

- каноническое уравнение гиперболы с центром в начале координат.

- уравнение гиперболы со смещённым центром O₁ ( x₀, y₀).

14. Каноническое уравнение параболы.

- каноническое уравнение параболы с вершиной в т. O (0,0).

- уравнение директрисы.

- уравнение параболы со смещённой вершиной в т. O₁ (x₀,y₀)

2. Примеры решения задач.

Задача 1. Даны координаты вершин треугольника АВС: А (4; 3), В (16; - 6), С (20; 16). Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и ВС и их угловые коэффициенты; 3) угол В в радианах с точностью до двух знаков; 4) уравнение высоты CD и ее длину; 5) уравнение медианы АЕ и координаты точки К пере­сечения этой медианы с высотой CD; 6) уравнение пря­мой, проходящей через точку К параллельно стороне АВ; 7) координаты точки М, расположенной симметрич­но точке А относительно прямой CD.

Решение. 1. Расстояние d между точками А ( x₁; y₁) и В (х₂; y₂) определяется по формуле:

(1)

Применяя (1), находим длину стороны АВ: =15

2. Уравнение прямой, проходящей через точки А(х₁; у₁) и В(х₂; y₂), имеет вид:

(2)

Подставляя в (2) координаты точек A и В, получим уравнение стороны АВ:

4y-12= -3x+12;

3x+4y-24=0 (AB).

Решив последнее уравнение относительно у, находим уравнение стороны АВ в виде уравнения прямой с уг­ловым коэффициентом:

4y= -3x+24; откуда

Подставив в (2) координаты точек В и С, получим уравнение прямой BC:

;

или y=5,5x-94, откуда k_BC=5,5.

3. Известно, что тангенс угла между двумя прямы­ми, угловые коэффициенты которых соответственно рав­ны k₁ и k₂ вычисляется по формуле:

(3)

Искомый угол В образован прямыми АВ и ВС, угло­вые коэффициенты которых найдены: Применяя (3), получим

В=63°26'. или В 1,11 рад.

4. Уравнение прямой, проходящей через данную точ­ку в заданном направлении, имеет вид: y—y₁ = k(x—x₁). (4)

Высота CD перпендикулярна стороне АВ. Чтобы найти угловой коэффициент высоты CD, воспользуемся усло­вием перпендикулярности прямых. Так как, , то . Подставив в (4) координаты точки С и най­денный угловой коэффициент высоты, получим:

Чтобы найти длину высоты CD, определим сперва координаты точки D-~ точки пересечения прямых АВ и CD. Решая совместно систему:

, находим x=8, y=0, т.е D(8;0)

---

По формуле (1) находим длину высоты CD:

5. Чтобы найти уравнение медианы АЕ, определим сначала координаты точки Е, которая является середи­ной стороны ВС, применяя формулы деления отрезка на две равные части:

Следовательно, E (18;5).

Подставив в (2) координаты точек А и Е, находим уравнение медианы:

Чтобы найти координаты точки пересечения высоты CD и медианы АЕ, решим совместно систему уравнений:

x=11, y=4; K (11;4).

6. Так как искомая прямая параллельна стороне АВ, то ее угловой коэффициент будет равен угловому коэф­фициенту прямой АВ. Подставив в (4) координаты най­денной точки К и угловой коэффициент по­лучим:

7. Так как прямая АВ перпендикулярна прямой CD, то искомая точка М, расположенная симметрично точ­ке А относительно прямой CD, лежит на прямой АВ. Кроме того, точка D является серединой отрезка AM. Применяя формулы (5), находим координаты искомой точки М:

Треугольник ABC, высота CD, медиана АЕ, прямая KF и точка М построены в системе координат хОу на рис. 1.

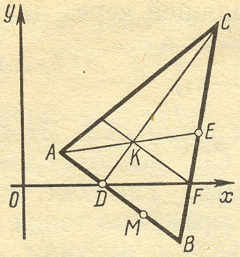
рис. 1

Задача 2. Составить уравнение геометрического мес­та точек, отношение расстояний которых до данной точ­ки A (4; 0) и до данной прямой х=1 равно 2.

Решение.

(x,y)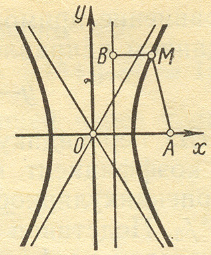

рис. 2

В системе координат хОу построим точку A (4;0) и прямую х=1. Пусть М(х; у) —произ­вольная точка искомого геометрического места точек. Опустим перпендикуляр MB на данную прямую х=1 и определим координаты точки В. Так как точка В лежит на заданной прямой, то ее абсцисса равна 1. Ордината точки В равна ординате точки М. Следовательно, В(1,у) (рис. 2).

По условию задачи МА:МВ=2. Расстояния МА и MB находим по формуле (1) задачи 1:

Возведя в квадрат левую и правую части, получим:

или

Полученное уравнение представляет собой гипербо­лу, у которой действительная полуось а=2, а мнимая -

Определим фокусы гиперболы. Для гиперболы вы­полняется равенство Следовательно, с²=4+12=16; с=4; F ₁(— 4; 0), F₂(4; 0) — фокусы гипер­болы. Как видно, заданная точка A(4; 0) является пра­вым фокусом гиперболы.

Определим эксцентриситет полученной гиперболы:

Уравнения асимптот гиперболы имеют вид и

Следовательно, или и — асимптоты гиперболы. Прежде чем постро­ить гиперболу, строим ее асимптоты.

Задача 3. Составить уравнение геометрического места точек, равноудаленных от точки A (4; 3) и прямой у=1. Полученное уравнение привести к простейшему виду.

Решение.

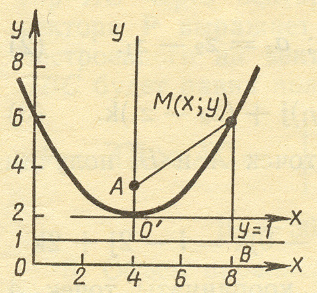
рис. 3

Пусть М(х; у) — одна из точек искомого геометрического места точек. Опустим из

точки М пер­пендикуляр MB на данную прямую у=1 (рис. 3). Опре­делим координаты точки В. Очевидно, что абсцисса точ­ки В равна абсциссе точки М, а ордината точки В равна I, т. е. В (х; 1). По условию задачи МА=МВ. Следовательно, для любой точки М(х; у), принадлежащей искомому геометрическому месту точек, справедливо равенство:

---

или

Полученное уравнение определяет параболу с верши­ной в точке О (4; 2). Чтобы уравнение параболы при­вести к простейшему виду, положим x-4=Х и y+2=Y; тогда уравнение параболы принимает вид:

Чтобы построить найденную кривую, перенесем нача­ло координат в точку О' (4; 2), построим новую систему координат XO'Y, оси которой соответственно парал­лельны осям Ох и Оу, и затем в этой новой системе построим параболу (*) (рис. 3).

3. Вопросы для самопроверки.

1. Какое равенство называется уравнением прямой?

2. Как пройдёт прямая линия, если свободный член в этом уравнении равен нулю?

3. Как вычислить угол между двумя прямыми? Каковы условия параллельности и перпендикулярности прямых?

4. Как найти угловой коэффициент прямой, если известны две её точки?

5. Запишите уравнения прямых, совпадающих с осями координат.

6. Дайте определение окружности. Приведите уравнение

к каноническому виду. Назовите центр и радиус данной окружности.

7. Сформулируйте определение эллипса, гиперболы, параболы. Постройте линию в системе координат.

8. Дайте определение эксцентриситета для: а) эллипса, б) гиперболы, в) параболы.

Тема 3. Основы векторной алгебры.

Ефимов, гл. 7,8

Клетенник, гл. 8,9; Данко, гл. 2.

3.1 Операции над векторами.

1. - направленный отрезок.

2. Сложение векторов.

+

или

+

2. Вычитание векторов.

-

- или

2. Умножение вектора на число.

3

 | | |

-3

 | | |

2. Скалярное произведение.

1) · = )

2) · =P, P- число

3) =

4) =

Свойства:

1). · = -скалярное произведение векторов, заданных координатами.

2). cos = (проекция вектора на ). Поэтому

· =cos = =

3). = , = , где =

4). · =0, если 

5). = или -условие коллинеарности векторов.

6). Угол между векторами:

, - условие перпендикулярности двух векторов.

7). · = ·

8). ·

9).

2. Векторное произведение

удовлетворяет условиям:

1). и

2 ).

3). -образуют такую же ориентацию как

Свойства:

1). =

2). , где

3).

4). Если то

5).

6). Если , то

7.) - площадь параллелограмма.

-площадь треугольника.

8).

9).

2. Смешанное произведение.

1). -форма записи смешанного произведения.

---

2). =

3). Если -компланарны , то

4). , если

5).

Д₁ С₁

М A₁

В1

Д С

А В

, где V-объём параллелепипеда .

3. 2 Примеры решения задач.

Задача 5. Даны координаты вершин пирамиды ABCD: А (2; 1; 0), B (3; -1; 2), С (13; 3; 10), D (0; 1; 4). Требуется: 1) записать векторы и в системе орт и найти модули этих векторов; 2) найти угол между векторами и ; 3) найти проекцию вектора на вектор ; 4) найти площадь грани ABC; 5) най­ти объем пирамиды ABCD.

Решение. I. Произвольный вектор а может быть представлен в системе орт i, j, k следующей формулой;

(1)

где а_х, а_у, а_г — проекции вектора а на координатные оси Ох, Оу и Oz, а — единичные векторы, направле­ния которых совпадают с положительным направлением осей Ох, Оу и Oz. Если даны точки и то проекции вектора на координатные оси находятся по формулам:

(2)

Тогда

(3)

Подставив в (3) координаты точек A и В, получим вектор

Аналогично, подставляя в (3) координаты точек А и С, находим

Подставив в (3) координаты точек А и D, находим век­тор :

Если вектор задан формулой (1), то его модуль вы­числяется по формуле

(4)

Применяя (4), получим модули найденных векторов:

,

2. Косинус угла между двумя векторами равен ска­лярному произведению этих векторов, деленному на произведение их модулей. Находим скалярное произведение векторов и :

Модули этих векторов уже найдены: , Следовательно,

¢.

3. Проекция вектора на вектор равна скалярному произведению этих векторов, деленному на модуль вектора :

4. Площадь грани ABC равна половине площади па­раллелограмма, построенного на векторах и . Обозначим векторное произведение вектора на век­тор через вектор . Тогда, как известно, модуль вектора выражает собой площадь параллелограмма, построенного на векторах и , а площадь грани ABC будет равна половине модуля вектора:

_

кв. ед.

5. Объем параллелепипеда, построенного на трех не­компланарных векторах, равен абсолютной величине их смешанного произведения. Вычислим смешанное произ­ведение

Следовательно, объем параллелепипеда равен 144 куб. ед., а объем заданной пирамиды ABCD равен 24 куб. ед.

3. 3 Вопросы для самопроверки.

1. Дайте определение вектора.

2. Какие векторы называются равными?

3. Геометрическое и аналитическое толкование координат вектора.

4. Запишите модуль вектора между координатами.

5. Как выполняется сложение, вычитание, умножение вектора на число геометрически (рисунком) и аналитически (формулой).

6. Дайте определение базису пространства.

7. Запишите скалярное произведение двух векторов в векторной форме и между координатами перемножаемых векторов. То же для векторного и смешанного произведения.

8. Условия коллинеарности и компланарности векторов в векторной и координатной форме.

---

Смотрите также файлы

• ЛАБОРАТОРНАЯ 9.doc

• реферат Греческая цивилизация.doc

• freyd.docx

• Русский язык_КОНТРОЛЬНАЯ РАБОТА для заочников.docx

• Testy_Fizika_tekhnologichesky.docx