Тема 4. Введение в анализ.

Пискунов, гл 1, § 1-9, упр 1-9, 39, 40

Гл 2, § 1-5, упр 1-6, 9-29, § 6-8,

Упр 31-35, 41-48, § 9, 10, упр 57-59

§ 11, упр 60-62.

1. Понятие предела.

Определение. Число а называется пределом функции y =f(x) в т. _{если для любого сколько угодно малого наперёд заданного ε >0 найдётся такое δ>0 (δ=δ(ε)), что выполняется неравенство < при <}

Этот факт записывается так:

_{Если , то говорят, что функция имеет пределом число a на бесконечности (x→∞).}

_{Если , то функцию называют бесконечно большой величиной в окрестности т..}

_{Если , то f(x)- бесконечно большая величина на бесконечности (x→∞).}

_{Если , то - бесконечно малая функция (величина) в окрестности т. X0 .}

_{Если , то - бесконечно малая величина на бесконечности (x→∞).}

_{При вычислении пределов используются теоремы о пределах, а также 1-ый замечательный предел}

_{второй замечательный предел , а также формулы ,}

_{4.2 Способы раскрытия неопределённостей видаи .}

I. Если _{то можно использовать три способа раскрытия этой неопределённости.}

1-ый способ. Разложить и числитель и знаменатель дроби на множители, затем сократить на общий множитель.

_{Пример.}

_{Ответ: где 2- предельное значение аргумента, (-1) -}

_{предельное значение функции y.}

2-ой способ. Использовать правило Лопиталя, т.е использовать равенство:

Пример:

_{3-ий способ. Применить таблицу эквивалентности бесконечно малых.}

_{Таблица.}

_1.

2.

3.

4.

Пример: Найти

Решение.

II. Если _{то можно использовать три способа раскрытия этой неопределённости.}

1-ый способ. Использовать правило Лопиталя.

Пример. Найти

_{Решение:}

2-ой способ. Разделить все слагаемые числителя и все слагаемые знаменателя на старшую переменную дроби.

Пример. Найти _[ -бесконечно малые величины ]=

Ответ:

2. Первый и второй замечательные пределы.

1. _{- первый замечательный предел.}

Замечание. При x0 sin x~ x

Пример 1.

Найти

_{если заменить , т.к , то}

Заметим,что показатель степени обратен по величине второму слагаемому в основании.

Пример 2. _{представили основание в виде суммы 1 и некоторой бесконечно малой величины.}

Выполненные тождественные преобразования в показателе степени, позволяют выделить 2-ой замечательный предел. ( в квадратных скобках)

3. Непрерывность функции. Точки разрыва.

Определение 1. Функция _{называется непрерывной в точке x0 , если выполняется равенство:}

_{Определение 2. Функция называется непрерывной в точке x0, если}

_{где соответственно приращение аргумента и приращение функции.}

Пример. Дана функция

Требуется : 1). Найти точку разрыва данной функции.

2). Найти _и

3). Найти скачок функции в точке разрыва.

---

Решение.

Данная функция определена и непрерывна в

При x=1 функция терпит разрыв, т.к меняется аналитическое выражение функции.

y

x=1- точка разрыва первого рода.

Скачком функции называется абсолютная величина разности между её правым и левым предельными значениями т.е _{(ед). –скачок функции.}

4. Вопросы для самопроверки.

1. Дайте определение функции, области определения. Приведите примеры.

2. Сформулируйте определение предела функции в точке.

3. Какая переменная величина называется бесконечно малой? Бесконечно большой в точке и на бесконечности

4. Что означают выражения: _{где C-const ?}

5. Приведите пример бесконечно малой функции в т. x=2 и бесконечно большой функции в этой же точке (аналитический и графический).

6. Каким свойством обладает приращение аргумента и приращение функции, если функция непрерывна в точке x₀ ?

Тема 5. Производная и дифференциал функции одного аргумента.

Пискунов, гл. III, § 1-26, упр 1-220

Гл. IV, § 1-7, упр 1-55.

5. 1 Определение производной, дифференциала.

1. Определение. Производной первого порядка от функции _{по аргументу x называется предел отношения приращения функции к приращению аргумента при условии, что , т.е. или}

2. _{, где - угол наклона касательной к}

_{- уравнение касательной, проведённой в т.}

3. _{- скорость изменения функции в т. x0.}

4. Отыскание производной называется дифференцированием.

5. _{- дифференциал функции равен произведению производной функции на дифференциал аргумента.}

Геометрически dy представляет собой приращение ординаты касательной к графику функции в заданной точке.

6. _{- дифференциал аргумента равен приращению аргумента.}

_{- дифференциал функции и приращение функции равны лишь приближённо.}

7. _{- формула для приближённых вычислений.}

Таблица дифференциалов и производных основных элементарных функций.

Элементарные функции	дифференциал	производная
1	2	3
1. Степенная функция
2. Линейная функция a,b-постоянные y=x.
3.Тригонометрич. функции y=sin x y=cos x y=tg x y=ctg x
4. Показательная функция , a-число
5. Логарифмическая функция y=ln x
6. Иррациональная функция

1	2	3
7. Обратно тригонометричес- кие функции y= arcsin x y=arcos x y= arctg x y=arcctg x
8. y=c c-const	d(c)=0·dx

---

Основные правила дифференцирования.

Пусть С- постоянное, _{и - функции имеющие производные.}

_{Тогда :}

₁₎

₂₎

₃₎

₄₎

₅₎

₆₎

_{7) если , , т.е , где функции f (U) и U (x) имеют производные, то - правило дифференцирования сложной функции.}

2. Примеры решения задач.

Задача 1. Найти производные _{или следующих функций:}

_а)

_б)

_в)

_г)

Решение:

а) Пользуясь правилом логарифмиро­вания корня и дроби, преобразуем правую часть:

Применяя правила и формулы дифференцирования, получим:

б) Предварительно прологарифмируем по основанию е обе части равенства:

Теперь дифференцируем обе части, считая сложной функцией от переменной х:

_откуда

в) В данном случае зависимость между аргументом х и функцией у задана уравнением, которое не разре­шено относительно функции у. Чтобы найти производ­ную у', следует дифференцировать по х обе части задан­ного уравнения, считая при этом у функцией от х, а за­тем полученное уравнение решить относительно искомой производной у'. Имеем

Из полученного равенства, связывающего х, у, и у',

находим производную у':

откуда

г) Зависимость между переменными х и у задана па­раметрическими уравнениями. Чтобы найти искомую производную у', находим предварительно дифференци­алы dy и dx и затем берем отношение этих дифферен­циалов

Задача 2. Найти производную второго порядка

а)

б)

Решение: а) Функция у задана в неявном виде. Дифференцируем по х обе части заданного уравнения, считая при этом у функцией от х:

(1)

откуда

Снова дифференцируем по х обе части (1):

(2)

Заменив у' в (2) правой частью (1), получим:

б) Зависимость между переменными x и у задана параметрическими уравнениями. Чтобы найти произ­водную у', находим сперва дифференциалы dy и dx и за­тем берем отношение этих дифференциалов:

Тогда

Производная второго порядка . Следователь­но, чтобы найти у", надо найти дифференциал dy':

_Тогда

Задача 3. Найти приближенное значение функции при исходя из ее точного зна­чения при

Решение: Известно, что дифференциал dy функ­ции представляет собой главную часть прира­щения этой функции .Если приращение аргумента мало по абсолютной величине, то приращение при­ближенно равно дифференциалу, т. е. . Так как , а то имеет место при­ближенное равенство:

Пусть , т. е.

Тогда

и

(1)

ли

Приближенное равенство (1) дает возможность найти значение функции при , если известно значение функции и ее производной при Прежде чем воспользоваться приближенным равен­ством ( 1 ) , находим числовое значение производной f'(x) при х= 6:

_или

_{Применяя (1), получаем}

3. _{Вопросы для самопроверки.}

1. Сформулировать определение производной.

2. Каков геометрический смысл производной?

3. Как составить уравнение касательной?

4. Каков геометрический и механический смысл производной?

5. Как найти производную неявной функции? Параметрической функции?

6. Функция непрерывна в т. x_0. Следует ли отсюда дифференцируемость функции?

7. В чём заключается геометрический смысл дифференциала функции?

8. Записать формулу, используемую в приближённых вычислениях. Найти приближённое значение

---

Тема 6. Приложения производной к исследованию поведения функции и построению графика и к другим задачам.

Пискунов, гл. V, §1-12, упр 1-134

Данко , ч. I, гл. 3

0. План исследования функции и построения графика.

1. Найти область определения функции. Решение этого вопроса указывает на те интервалы оси (ОХ), над которыми пройдёт график и на те значения аргумента x, над которыми график не пройдёт, а также в каких точках пройдут вертикальные асимптоты.

2. Исследовать на чётность, нечётность. Решение этого вопроса облегчает построение.

3. Указать промежутки монотонности функции и найти экстремумы её, точки экстремумов. Построить соответствующие точки на координатной плоскости.

4. Указать точки перегиба графика функции и нанести их на координатную плоскость. Указать промежутки выпуклости, вогнутости.

5. Найти уравнения вертикальных и наклонных асимптот, используя условия для существования этих асимптот. Построить эти линии на координатной плоскости.

6. Найти точки пересечения графика функции с осями координат. Нанести их на плоскость.

7. Исследовать поведение функции на концах области определения. Это поможет при построении графика.

8. Можно взять несколько контрольных точек, в случае уточнения поведения графика.

9. Построить график.

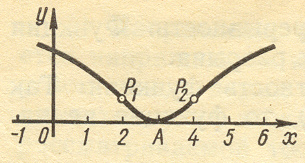
Задача 1. Исследовать функцию у = 1п(х² — 6х +10) и построить ее график.

Решение:

1. Определим область существования функции. Квадратный трехчлен, стоящий под знаком ло­гарифма, можно представить так: х²—6x+10=(x-3)² + 1. Как видно, под знаком логарифма будет положи­тельное число при любом значении аргумента х. Следо­вательно, областью существования данной функции слу­жит вся числовая ось.

2. Исследуем функцию на непрерывность. Функция всюду непрерывна и не имеет точек разрыва.

3. Установим четность и нечетность функции. Так как у(-х)¹у(х) и у(- х)¹ - у(х), то функция не яв­ляется ни четной, ни нечетной.

4. Исследуем функцию на экстремум. Находим пер­вую производную:

Знаменатель х²- 6x+10>0 для любого значения х. Как видно, при х < 3 первая производная отрицательна, а при х > 3 положительна. При х = 3 первая производная меняет свой знак с минуса на плюс. В этой точке функ­ция имеет минимум:

Итак, A(3; 0) - точка минимума . Функция убывает на интервале (- ¥ , 3) и возрастает на интервале (3, + ¥).

5. Определим точки перегиба графика функции и интервалы выпуклости и вогнутости кривой. Для этого находим вторую производную:

Разобьем всю числовую ось на три интервала: ( - ¥, 2), (2, 4), (4, + ¥). Как видно, в первом и третьем интерва­лах вторая производная отрицательна, а во втором ин­тервале положительна. При x₁ = 2 и х₂ = 4 вторая произ­водная меняет свой знак. Эти значения аргумента явля­ются абсциссами точек перегиба. Определим ординаты этих точек:

Следовательно, P₁(2; ln 2) и P₂(4; ln 2) — точки перегиба графика функции. График является выпуклым в интерва­лах ( - ¥, 2) и (4, +¥) и вогнутым в интервале (2, 4).

---

6. Определим уравнения асимптот графика функции. Для определения уравнения асимптоты y=kx+b вос­пользуемся формулами:

Имеем

Чтобы найти искомый предел, дважды применяем правило Лопиталя:

Итак, кривая не имеет асимптот.

0. Использование производной в задачах прикладного характера.

Задача 1. Найти такой цилиндр, который имел бы наибольший объём при данной полной поверхности S.

Решение: Пусть радиус основания цилиндра равен x, а высота равна y.

Тогда

Следовательно, объём цилиндра выразится так:

Задача сводится к исследованию функции V(x) на максимум при x > 0.

Н

_{и приравняем её к нулю, откуда}

айдём производную

Найдём

П

_{выполняется условие}

_{,то объём имеет,}

ри

_{наибольшее значение причем}

_{т.е осевое сечение цилиндра должно быть квадратом.}

Ответ: Цилиндр с квадратным сечением имеет наибольший объём при данной полной поверхности S.

План действий при решении задач прикладного характера.

1. Обозначить некоторую неизвестную величину прикладной задачи переменной x.

2. Записать ту величину, которая должна быть по условию наименьшей ( наибольшей ) как функцию переменной x.

3. Исследовать полученную функцию на экстремум, используя производные 1-го порядка и второго порядка, найти значение x, соответствующее точке экстремума исследуемой функции.

4. Записать ответ, вернувшись к прикладному значению x.

0. Нахождение наибольшего и наименьшего значения функции на отрезке.

Задача. Найти наибольшее и наименьшее значения функции:

на сегменте -2; 2

Решение: Найдём критические точки и исследуем их на экстремум.

В точке x=0 функция имеет максимум, равный f(0)=3.

В каждой из точек x=-1 и x=1 функция имеет минимум, равный f (-1)=f (1)=2

Найдём значения функции на концах сегмента :

Итак , наибольшее значение равно 11, а наименьшее 2.

Задача . Найти радиус кривизны и координаты центра кривизны кривой в точке А (0; 1).

Решение: Радиус кривизны вычисляется по фор­муле:

Дважды дифференцируя данную функцию, находим

Вычислим значения производных у' и у" в заданной точке А (0; 1), т.е. при x = 0; имеем y¢(0) = 2; y¢¢ (0) = - 4.

Тогда радиус кривизны:

Для нахождения координат центра кривизны С(x_с; y_с] воспользуемся формулами:

Подставив в эти формулы координаты точки А и найден­ные значения производных, получим:

Итак, точка С (5/2; -1/4) — центр кривизны.

Кривая , точка А (0; 1), центр кривизны С (5/2; -1/4) и радиус кривизны R»2,8 .

Задача. Найти радиус кривизны кривой r = a sin3 j (трех лепестковая роза) в точке A (p/6; а).

Решение. Если кривая задана в полярной системе координат уравнением r=f (j), то ра­диус кривизны вычисляется по фор­муле:

Дважды дифференцируя данную функ­цию r= a sin 3j , найдем

---

Смотрите также файлы

• ЛАБОРАТОРНАЯ 9.doc

• реферат Греческая цивилизация.doc

• freyd.docx

• Русский язык_КОНТРОЛЬНАЯ РАБОТА для заочников.docx

• Testy_Fizika_tekhnologichesky.docx