ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 73
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Методы управленческих решений
Задание 36.1
Решить и проанализировать задачу одномерной нелинейной оптимизации. Определить х при которых достигается минимум и максимум функции (60 %). Определить минимальное и максимальное значение функций (30 %).
f(x)→ extr
f(x) =
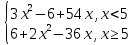
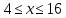
Кратко ответить на вопросы и продемонстрировать ответ на примере своего решения:
-
В каких точках необходимо искать локальные экстремумы функций одной переменной? Покажите это на примере своего решения (15 %) -
Что такое локальный экстремум? Покажите это на примере своего решения (15 %)
Решение:
1) Определим градиент функции. В данном случае функции одной переменной градиент совпадает с производной. Функция задана разными выражениями на разных интервалах, поэтому нужно взять производные для каждого интервала. Они будут справедливы при строгом выполнении ограничивающих интервалы неравенств:
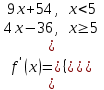
2) Определим точки, где производная равна нулю. Для этого определим все x, удовлетворяющие равенствам:
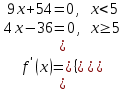
Рассмотрим интервал
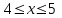 . На нем имеем уравнение:
. На нем имеем уравнение: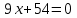 .
.Решая уравнение, находим:
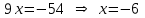 .
.Однако данное значение не попадает в интервал:
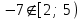 . Значит, на указанном интервале нулей производной нет.
. Значит, на указанном интервале нулей производной нет. Рассмотрим интервал
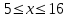 . На нем имеем уравнение:
. На нем имеем уравнение: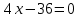 .
.Решая уравнение, находим:
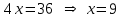 .
.Данное значение принадлежит рассматриваемому интервалу:
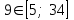 .
.Таким образом,
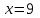
является корнем производной. Определим значение функции в этой точке:
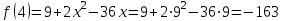
3) Определим значение функции в точках границ области:
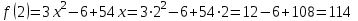 ;
;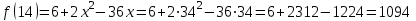 .
.Таким образом, наибольшее значение функции
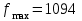 достигается при
достигается при 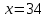 . Наименьшее значение функции
. Наименьшее значение функции 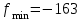 достигается при
достигается при 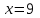
Ответ:
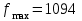 при
при 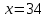 ;
; 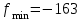 при
при 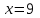 .
.Задание 36.2
Торговое предприятие занимается поставками овощей. Закупочная цена одного ящика овощей равна 1350 рублей. Стоимость доставки определяется в основном арендой автопоезда и равна 72900 рублей за доставку, заказ доставляется за 10 дней. За месяц предприятие реализует примерно 90 ящиков овощей. Затраты на хранение ящика составляет 180 рублей в месяц.
Руководитель предприятия ставит задачу оптимизировать совокупные издержки по организации поставок. На основе модели Уилсона для бизнес – процесса управления запасами определите оптимальные параметры поставки. В ответах укажите единицы измерения найденных величин.
1) Сколько ящиков нужно привозить за один раз?
2) Как часто нужно осуществлять поставки?
3) Сколько времени будет проходить между поставками?
4) Какова величина запаса овощей при подаче очередного заказа?
5) Каковы суммарные годовые затраты на организацию поставок?
6) Будет ли выгодно закупать товар со скидкой 8% если объем закупки будет составлять не менее 600 ящиков сразу? Ответ обоснуйте.
7) Какие расходы и как изменились при использовании скидки? Обоснуйте выбор «использовать или не использовать скидку» на основе сопоставления этих расходов.
Решение:
Определяем входящие параметры системы:
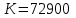 руб.;
руб.;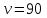
ящ./мес.;
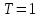 мес.;
мес.;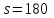 руб./ящ.мес.;
руб./ящ.мес.;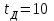 дня. Эту величину необходимо перевести в месяцы:
дня. Эту величину необходимо перевести в месяцы: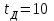 дня =
дня = 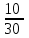 мес.= 0,33 мес.
мес.= 0,33 мес.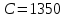 руб.
руб.1) Определим, сколько ящиков нужно привозить за один раз.
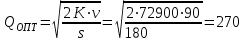 ящиков.
ящиков.2) Определим, как часто нужно осуществлять поставки.
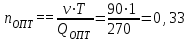 поставок в месяц.
поставок в месяц.3) Определим, сколько времени будет проходить между поставками.
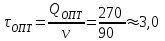 мес.
мес. 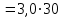 дн. = 90 дней.
дн. = 90 дней.Вывод: необходимо организовать поставки по 270 ящиков каждые 90 дней (с частотой 0,3 поставок в месяц).
4) Определим, какова величина запаса овощей при подаче очередного заказа.
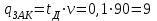 .
.Таким образом, заказ необходимо делать в момент, когда в наличие осталось 9 ящиков овощей.
5) Определим, каковы суммарные годовые затраты на организацию поставок.
Определим затраты на доставку:
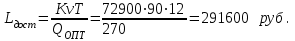
Затраты на хранение:
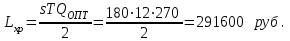
Затраты на приобретение заказа:
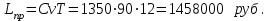
Суммарные расходы на поставку и хранение овощей:
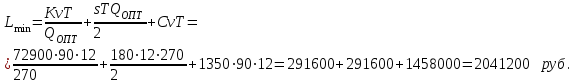 Суммарные расходы на поставку и хранение овощей составят 2041200 руб. за 12 месяцев.
Суммарные расходы на поставку и хранение овощей составят 2041200 руб. за 12 месяцев.6) Определим, будет ли выгодно закупать товар со скидкой 8% если объем закупки будет составлять не менее 600 ящиков сразу.
Так как
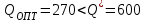 , то найдем
, то найдем 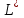 по формуле:
по формуле: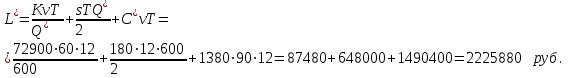 Так как
Так как 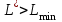 , то закупать 600 ящиков товара со скидкой 8% не выгодно.
, то закупать 600 ящиков товара со скидкой 8% не выгодно.
7) При использовании скидки изменились затраты на доставку:
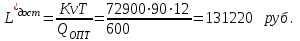
При сравнении значений затрат на доставку без скидки и при использовании скидки получаем:
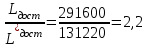 .
.Таким образом, при использовании скидки затраты на доставку уменьшились в два раза.
При использовании скидки также изменились затраты на хранение:
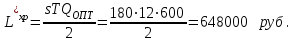
При сравнении значений затрат на хранение без скидки и при использовании скидки получаем:
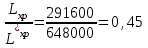
Таким образом, при использовании скидки затраты на хранение увеличились в два раза.
При использовании скидки также изменились затраты на приобретение заказа:
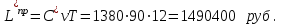
При сравнении значений затрат на приобретение заказа без скидки и при использовании скидки получаем:
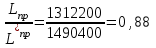 .
.Таким образом, при использовании скидки затраты на приобретение заказа уменьшились на 8,8%.
Суммарные расходы на поставку и хранение овощей при использовании скидки возросли на 291600 руб., поэтому закупать 600 ящиков товара со скидкой 8% не выгодно.
Список использованной литературы
-
Балдин К.В. Управленческие решения: Учебник / Балдин К.В., Воробьев С.Н., Уткин В.Б.. – М.: «Дашков и К°», 2012. - 496 с. -
Соловьев В. И. Методы оптимальных решений. – М.: Финансовый университет, 2012. – 364 с. -
Юкаева В. С. Принятие управленческих решений: учебник / В.С.Юкаева, Е.В.Зубарева, В.В.Чувикова – М.: "Дашков и К", 2012. – 324с.