Файл: Практическое занятие 13. Проверка гипотезы о законе распределения на основе критерия Пирсона (распределение в виде равноотстоящих вариант и соответствующих им частот). Цель.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 52
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практическое занятие № 13.
Проверка гипотезы о законе распределения на основе критерия Пирсона (распределение в виде равноотстоящих вариант и соответствующих им частот).
Цель: научится
- применять критерий Пирсона при решении задач на проверку гипотезы о законе распределения, если распределение задано в виде равноотстоящих вариант и соответствующих им частот.
Теоретические сведения
Существуют различные методы проверки гипотез о неизвестных параметрах известных законов распределения. Но чаще на практике закон распределения неизвестен, и необходимо выбрать модель закона и проверить возможность принять выдвинутую модель.
Проверка гипотезы о предполагаемом законе осуществляется с помощью специально подобранной случайной величины, которая называется критерием согласия.
Критерий согласия - это критерий проверки гипотезы о предполагаемом законе неизвестного распределения.
Критерий Пирсона (c2) можно применять для проверки любого закона распределения. В этом состоит его преимущество.
Эмпирические и теоретические частоты обычно различаются. Это различие может быть случайным (незначимым) или неслучайным (значимым). Если различия неслучайны, то выдвинутая нулевая гипотеза неверна.
Критерий Пирсона позволяет ответить на вопрос о значимости или незначимости различий.
Пусть на основании эмпирического распределения выдвинута Н0: генеральная совокупность имеет нормальное распределение.
В качестве критерия проверки принимается случайная величина
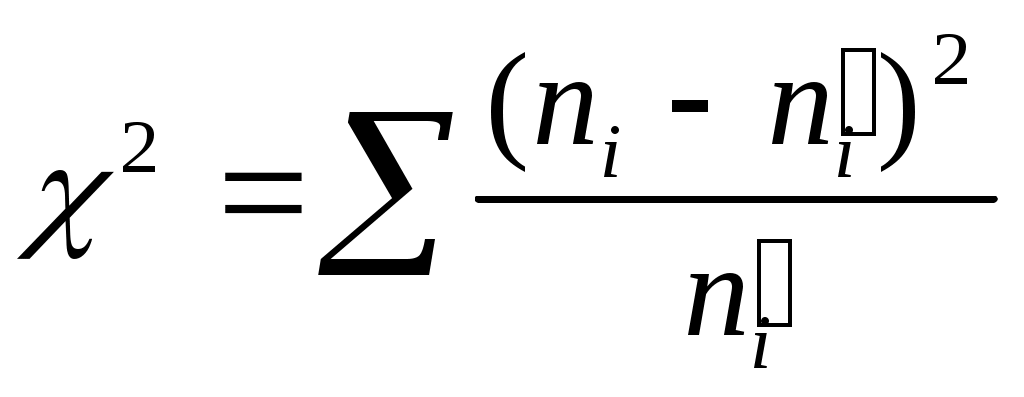
Приведем алгоритм вычисления теоретических частот, если выборка представлена дискретным рядом:
1. Находят параметрические оценки нормального закона: среднее выборочное и выборочное среднее квадратическое отклонение;
2. Вычисляют теоретические частоты по формуле:
, где h- разность между соседними вариантами (шаг),n – объем выборки (сумма всех частот)
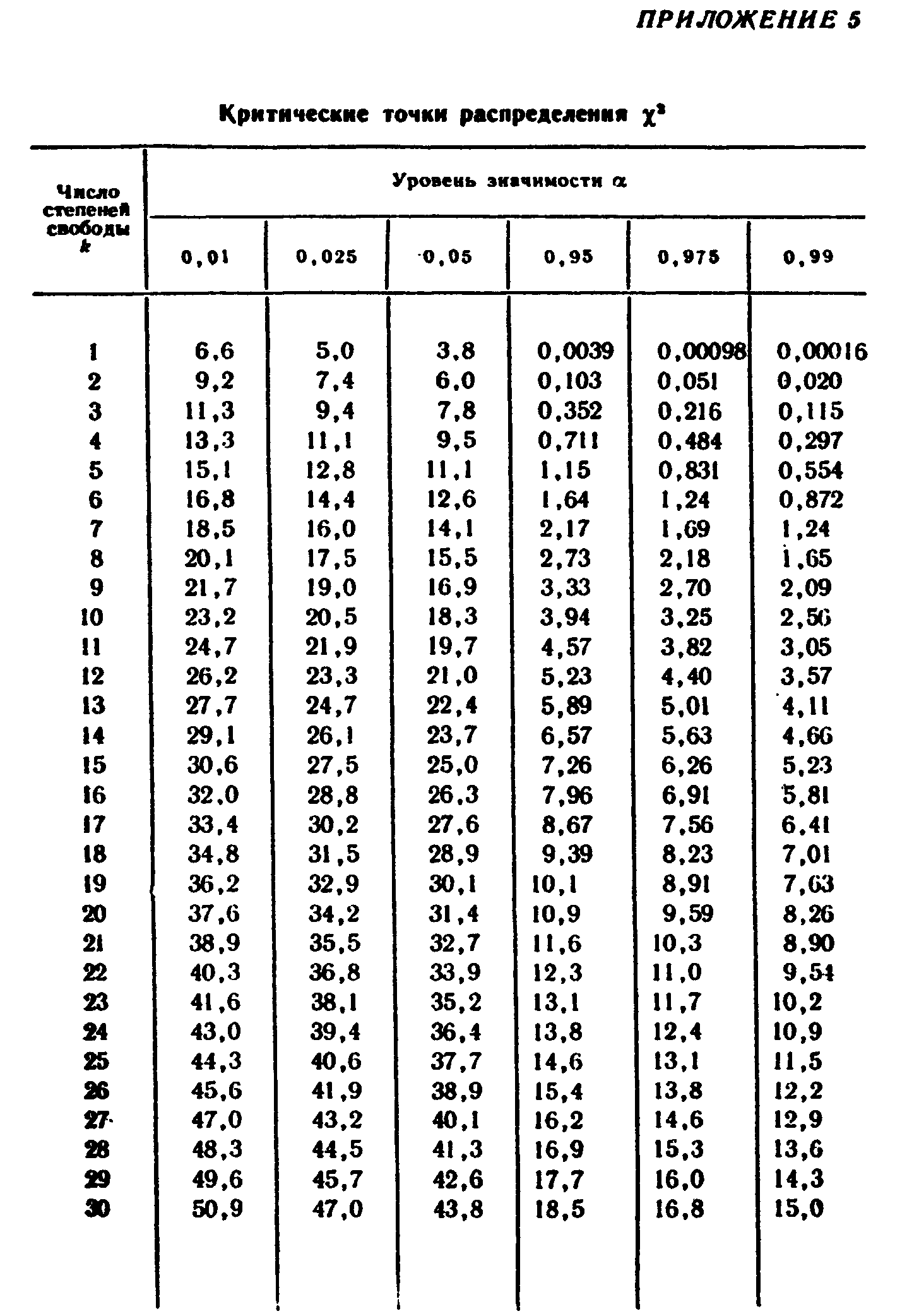
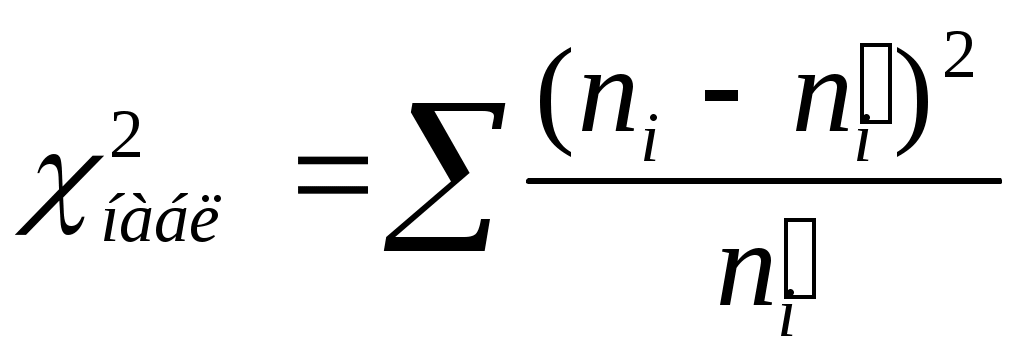- это наблюдаемое значение критерия. Для ответа на вопрос о принятии нулевой гипотезы необходимо найти теоретическое значение критерия – критическую точку c2кр . Его выбирают по «Таблице критических точек c2» в зависимости от принятого уровня значимости a и числу степеней свободы k=s -1- r, где s – число групп (частичных интервалов), r- количество параметров предполагаемого распределения. Для нормального закона r = 2, тогда k =s –3.
Далее сравнивают наблюдаемое значение критерия с теоретическим : если наблюдаемое значение критерия меньше теоретического
, то нулевую гипотезу принимают, в противном случае- отвергают. Примеры решения задач
Задача 1. При уровне значимости 0,05 проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты:
-
Эмп.частоты
6
13
38
74
106
85
30
14
Теорет. частоты
3
14
42
82
99
76
37
13
Решение. Вычислим
, для чего составим расчетную таблицу:-
i
ni
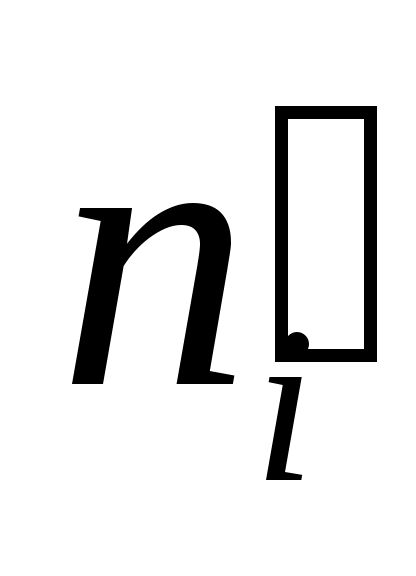
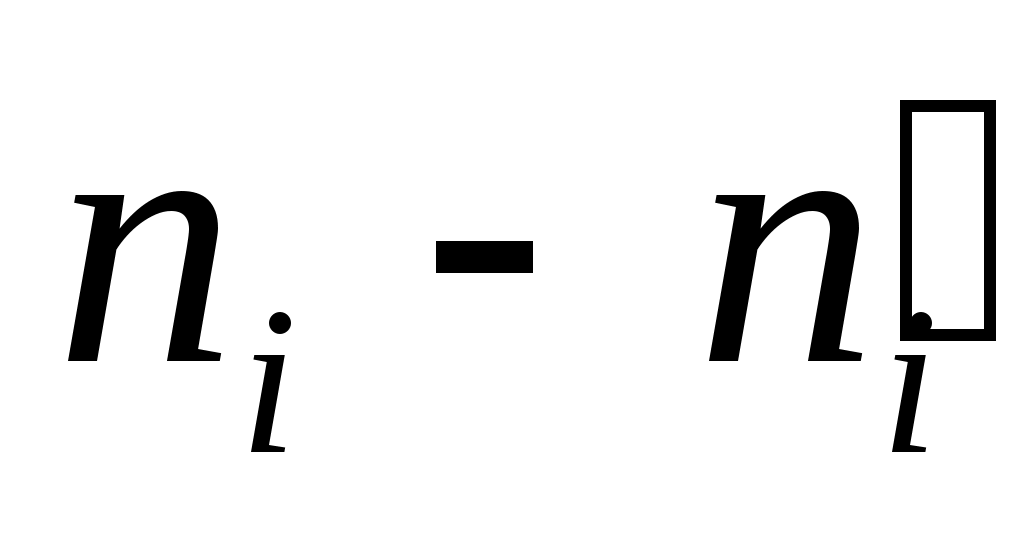
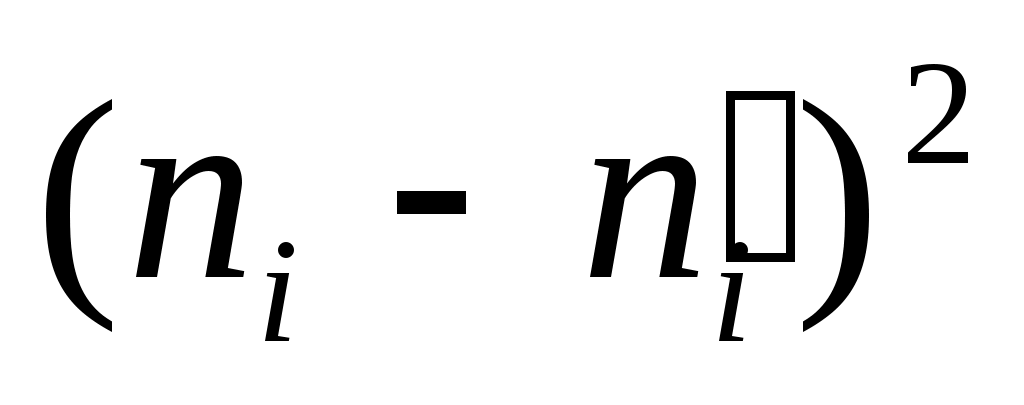
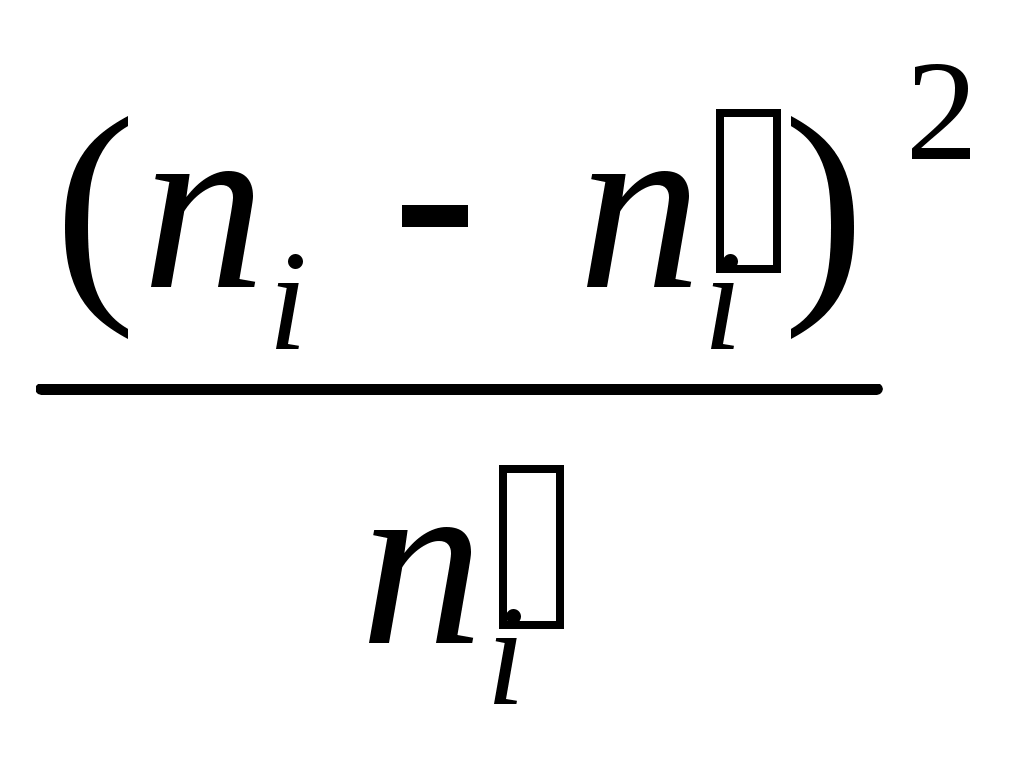
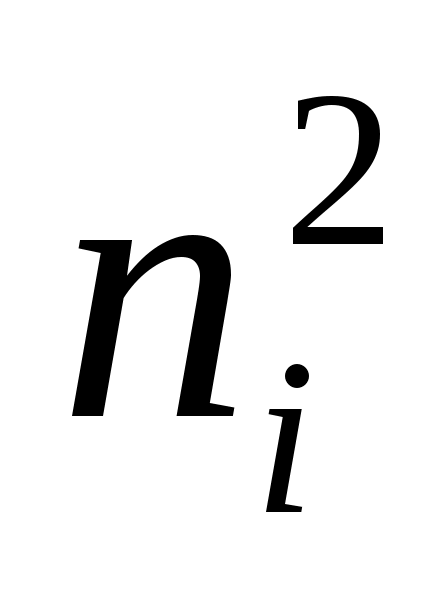
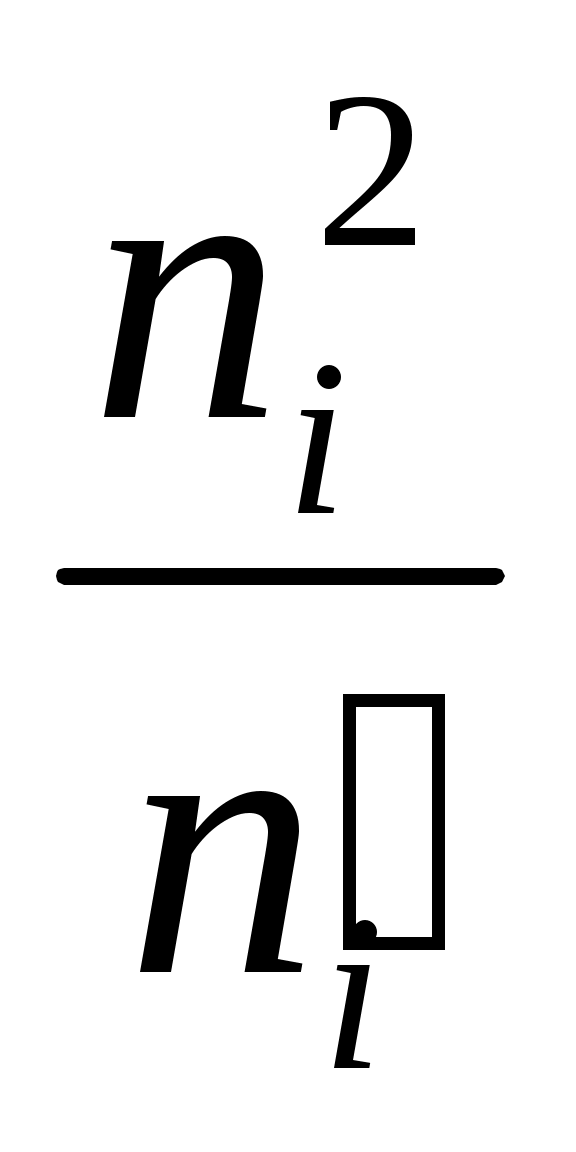
1
6
3
3
9
3
36
12
2
13
14
-1
1
0,07
169
12,07
3
38
42
-4
16
0,38
1444
34,38
4
74
82
-8
64
0,78
5476
66,78
5
106
99
7
49
0,49
11236
113,49
6
85
76
9
81
1,07
7225
95,07
7
30
37
-7
49
1,32
900
24,32
8
14
13
1
1
0,08
196
15,08
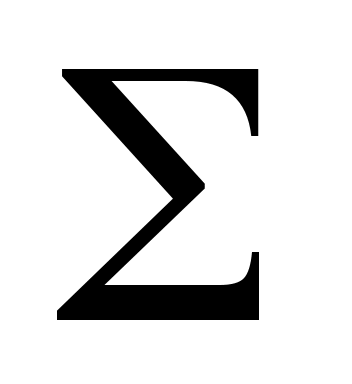
366
366
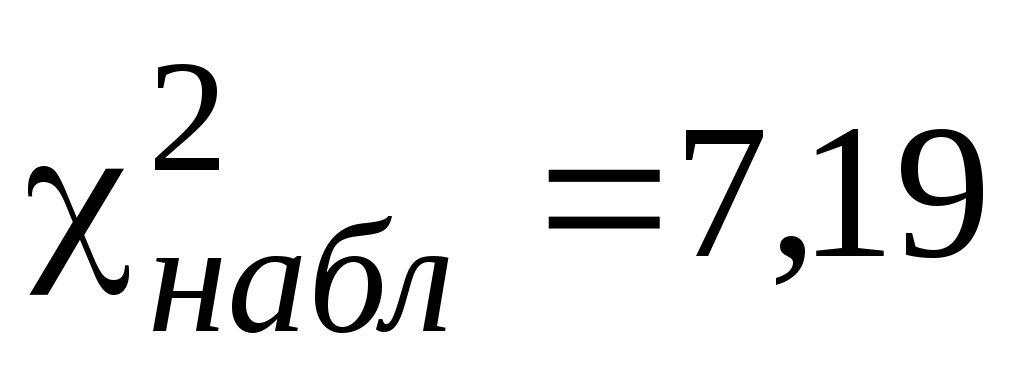
373,19
Контроль:
: 
- n=373,19-366=7,19. Вычисления произведены правильно.Найдем число степеней свободы, учитывая, что число групп выборки s=8; k=8-3=5. По таблице критических точек распределения
, по уровню значимости 
и числу степеней свободы k=5 находим 
.Так как
- нет оснований отвергнуть нулевую гипотезу. Другими словами, расхождение эмпирических и теоретических частот незначимо. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.Задача 2. Используя критерий Пирсона, при уровне значимости 0,05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности X с эмпирическим распределением выборки объема n=200:
-
xi
5
7
9
11
13
15
17
19
21
ni
15
26
25
30
26
21
24
20
13
Решение. Используя метод произведений, найдем выборочную среднюю
=12,63 и выборочное среднее квадратичное отклонение 
=4,695Составим расчетную таблицу:
-
i
xi
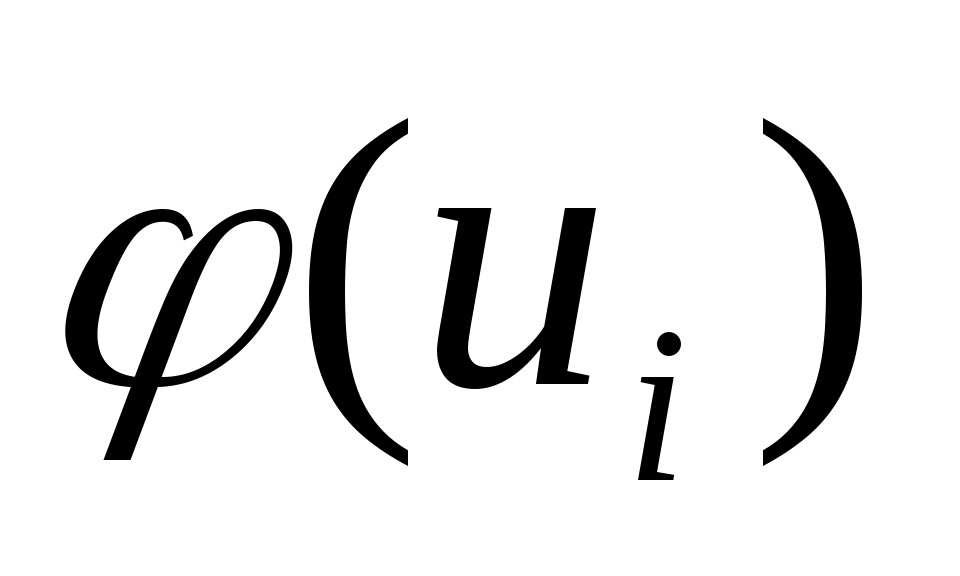
ni
1
5
-1,62
0,1074
9,1
15
5,9
34,81
3,8
2
7
-1,20
0,1942
16,5
26
9,5
90,25
5,5
3
9
-0,77
0,2966
25,3
25
-0,3
0,09
0,0
4
11
-0,35
0,3752
32,0
30
-2,0
4,00
0,1
5
13
0,08
0,3977
33,9
26
-7,9
62,41
1,8
6
15
0,51
0,3503
29,8
21
-8,8
77,44
2,6
7
17
0,93
0,2589
22,0
24
2,0
4,00
0,2
8
19
1,36
0,1582
13,5
20
6,5
42,25
3,1
9
21
1,78
0,0818
7,0
13
6,0
36,00
5,1
200
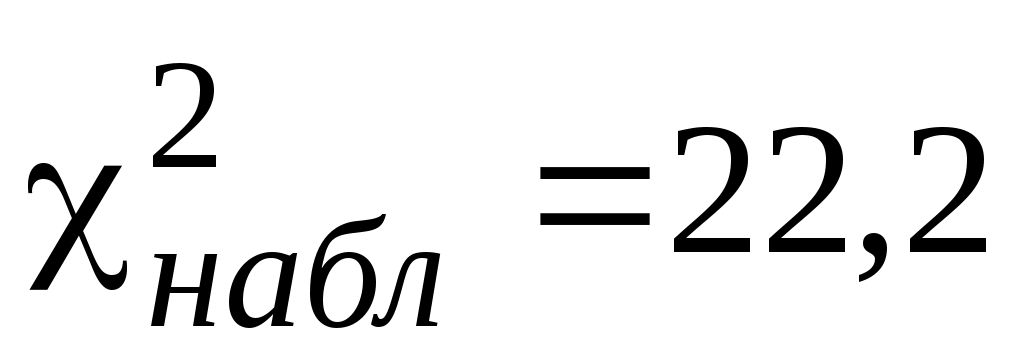
По таблице критических точек распределения
, по уровню значимости 
и числу степеней свободы k=6 находим 
.Так как
- гипотезу о нормальном распределении генеральной совокупности отвергаем. Другими словами, эмпирические и теоретические частоты различаются значимо.Задания для самостоятельной работы
1 вариант
1. При уровне значимости 0,05 проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты:
ni 6 12 16 40 13 8 5
4 11 15 43 15 6 62. Используя критерий Пирсона, при уровне значимости 0,05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности X с эмпирическим распределением выборки объема n=200:
xi 5 7 9 11 13 15 17 19 21
ni 10 22 20 30 26 20 24 13 20
2 вариант
1. При уровне значимости 0,05 проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты:
ni 5 13 12 44 8 12 6
2 20 12 35 15 10 62. Используя критерий Пирсона, при уровне значимости 0,05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности X с эмпирическим распределением выборки объема n=200:
xi 0,3 0,5 0,7 0,9 1,1 1,3 1,5 1,7 1,9
ni 6 9 26 25 30 26 21 29 28
3 вариант
1. При уровне значимости 0,05 проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты:
ni 14 18 32 70 20 36 10
10 24 34 80 18 22 122. Используя критерий Пирсона, при уровне значимости 0,05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности X с эмпирическим распределением выборки объема n=200:
xi 5 7 9 11 13 15 17 19 21
ni 13 26 26 30 25 20 24 21 15
