Файл: Решение уравнения будем искать в виде y erx. Для этого составляем характеристическое уравнение.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 20
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Следовательно, ряд:
сходится. -
Задание4
Исследовать сходимость ряда с помощью признака Даламбера:
Применим радикальный признак Коши:
Поскольку:
Получаем:
Поскольку полученное значение меньше 1, то ряд сходится.
Признак Даламбера.
при q < 1 - ряд сходится, q > 1 - ряд расходится, q = 1 - получаем неопределенность (дополнительные исследования).
=
=
=
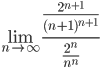=0
Поскольку q < 1, то ряд сходится.
Следовательно, ряд:
сходится. -
Задание5
Исследовать сходимость ряда с помощью признака Коши:
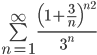
В силу свойств второго замечательного предела, исходное выражение можно упростить:
Проверим необходимое условие сходимости ряда (равенства предела 0):
Предел не равен 0, поэтому ряд расходится.
-
Задание6
Исследовать сходимость ряда с помощью интегрального признака:
Применим сравнительный признак.
Рассмотрим ряд
vn=
Поскольку un≤vn, то если ряд vn будет сходиться, то будет сходиться и исходный un.
Поскольку α=1.50000000000000>1, то ряд сходится.
Исследуем сходимость ряда при помощи интегрального признака сходимости Коши. Рассмотрим несобственный интеграл:
Представим исходный интеграл в виде:
Вычислим определенный интеграл:
Так как несобственный интеграл сходится, то сходится и исследуемый ряд.
Исследуем сходимость ряда при помощи интегрального признака сходимости Коши. Рассмотрим несобственный интеграл:
Представим исходный интеграл в виде:
Вычислим определенный интеграл:
Так как несобственный интеграл сходится, то сходится и исследуемый ряд.
Следовательно, ряд:
сходится.-
Задание7
Найти область сходимости степенного ряда:
Применим радикальный признак Коши:
Поскольку:
Получаем:
Поскольку полученное значение меньше 1, то ряд сходится.
Следовательно, ряд:
сходится.