ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 95
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Вариант №18
1.По проводнику, форма которого изображена на рисунке, течёт ток I = 2 А. Найти магнитную индукцию в т.О, если r = 0,5 см.
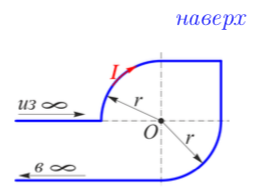
| Дано:   | Решение: 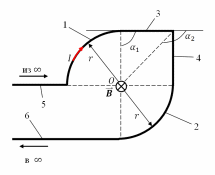 Покажем рисунок. Мысленно разделим проводник на шесть частей 1, 2, 3, 4, 5 и 6. По принципу суперпозиции индукция магнитного поля в центре 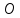 равна сумме индукций, создаваемых в этой точке каждой частью проводника: равна сумме индукций, создаваемых в этой точке каждой частью проводника: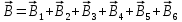 Часть 5 проводника в своём продолжении проходит через точку 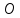 , следовательно, индукция , следовательно, индукция 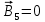 . Так как все векторы индукций направлены одинаково (в данном случае перпендикулярно плоскости чертежа от нас), то векторное равенство запишем в скалярном виде: . Так как все векторы индукций направлены одинаково (в данном случае перпендикулярно плоскости чертежа от нас), то векторное равенство запишем в скалярном виде: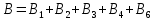 Индукция 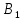 создаётся в центре создаётся в центре 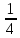 частью кругового тока радиуса частью кругового тока радиуса 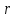 , следовательно, величина индукции равна: , следовательно, величина индукции равна: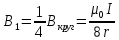 Индукция 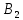 также создаётся в центре также создаётся в центре 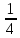 частью кругового тока радиуса частью кругового тока радиуса 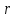 , следовательно, величина индукции равна: , следовательно, величина индукции равна: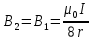 Определяем индукцию поля, создаваемого в точке 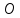 частью 3 проводника. Используем формулу для расчёта индукции поля, создаваемого отрезком проводника с током: частью 3 проводника. Используем формулу для расчёта индукции поля, создаваемого отрезком проводника с током: 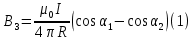 В нашем случае: 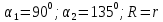 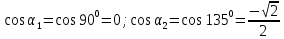 Тогда 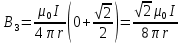 Часть 4 проводника расположена симметрично части 2 относительно центра 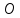 , следовательно, , следовательно, 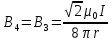 Индукция 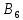 создаётся в центре создаётся в центре 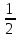 частью бесконечного прямолинейного проводника с током, следовательно, величина индукции равна: частью бесконечного прямолинейного проводника с током, следовательно, величина индукции равна: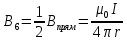 Суммарная индукция в точке 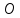 : :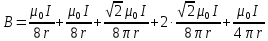 Или 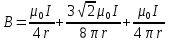 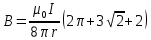 Вычисляем: 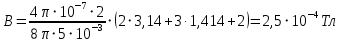 |
| Найти: 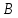 ― ? ― ? |
Ответ:
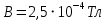
2.В плоскости магнитного меридиана Земли на вертикальной оси установлен виток радиусом R = 10 см таким образом, что ось совпадает с одним из его диаметров и виток может свободно вращаться. По витку течёт ток I = 10 А. При этом виток находится в начальном положении благодаря приложенному к нему механическому моменту М = 6,28 мкН*м. Определить горизонтальную составляющую магнитной индукции в данном точке планеты.
| Дано: R = 0,1 м I = 10 A M = 6,28∙10−6 Тл | Решение:  Покажем рисунок. Магнитный момент витка с током 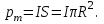 Механический момент, действующий на виток 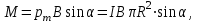 где α = 90° ― угол между векторами 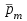 и и 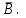 Отсюда индукция: 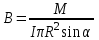 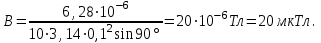 Для того, чтобы удержать рамку, нужно приложить такой же момент М, но в обратном направлении. |
| Найти: B ― ? |
Ответ: B = 20 мкТл.
3.Определить какой должна быть добротность LC-контура, чтобы частота, при которой наступает резонанс тока, отличалась от частоты, при которой наступает резонанс напряжения на конденсаторе, не более чем на 1%.
| Дано: 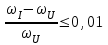 | Решение: Запишем частотную зависимость амплитудного значения напряжения и тока на элементах контура: 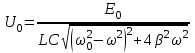 (1) (1)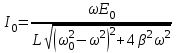 (2), где (2), где 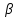 – коэффициент затухания; – коэффициент затухания; 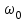 – собственная частота колебаний; – собственная частота колебаний; 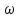 – частота затухающих колебаний контура. – частота затухающих колебаний контура.Исследуем выражение (1) на экстремум. Очевидно, что амплитуда колебаний будет максимальной в том случае, если подкоренное выражение в (1) будет минимальным. Обозначим подкоренное выражение через 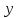 : :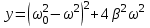 Запишем условие экстремума подкоренного выражения: 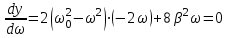 Отсюда: 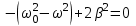 Отсюда: 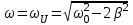 (3) (3)Найдем резонансную частоту для тока. Для этого формулу (2) перепишем в другом виде, учитывая следующие выражения для 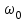 и и 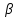 : :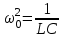 ; ; 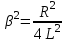 (4) (4)Учитывая (4), формулу (2) можем переписать так: 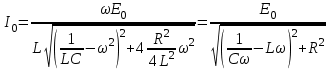 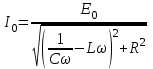 (5) (5)Отсюда видим, что амплитуда тока будет максимальна, если 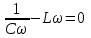 Отсюда: 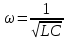 (6) (6)Из выражения (4) видим, что: 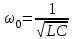 (7) (7)Тогда из выражений (6) и (7) можем записать, что 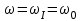 (8) (8)Согласно условию задачи 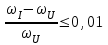 (9) (9)Подставим (3) и (8) в (9): 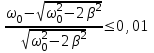 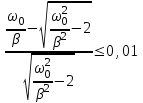 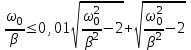 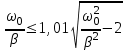 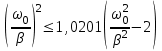 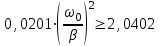 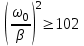 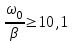 (10) (10)Добротность контура равна: 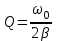 (11) (11)Выражение (6) можем записать так: 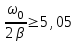 (12) (12)Из выражений (11) и (12) можем записать, что 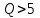 |
| Найти: 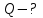 |
Ответ:
 .
.4.В интерферометре Майкельсона на пути одного из интерферирующих пучков света (λ=590 нм) поместили закрытую с обеих сторон стеклянную трубку длиной l=10 см, откачанную до высокого вакуума. При заполнении трубки хлористым водородом произошло смещение интерференционной картины. Когда хлористый водород был заменён бромистым водородом, смещение интерференционной картины возросло на ∆m=42 полосы. Определить разность ∆n показателей преломления бромистого и хлористого водорода.
| Дано: λ = 590 нм = 590∙10−9 м l = 10 см = 0,1 м ∆m = k = 42 | Решение: 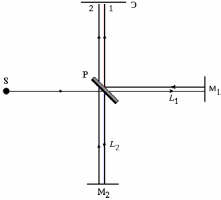 Покажем рисунок. М1, М2 ― зеркала; Э ― экран; Р ― полупрозрачная пластинка; S ― источник монохроматического света; L1, L2 ― пути первого и второго лучей, интерферирующих на экране. Луч проходит через трубку с хлором два раза. Поэтому разность хода лучей, проходящих в хлористом водороде и в бромистом водороде, равна 2(п2l− п1l) = 2l(n2−п1) = kλ. Отсюда 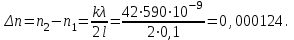 |
| Найти: Δn ― ? |
Ответ: n = 0,000124.
5.Параллельный пучок естественного света падает на плоскую поверхность стекла (n = 1,6). Отражённый свет полностью поляризован. Найти угол θ (в градусах) между отражённым и падающим пучками света в точке падения.
| Дано: n1 = 1 (воздух) n2 = 1,6 (стекло) | Решение: 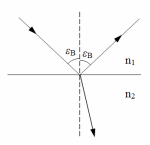 Так как отраженный свет полностью поляризован, то пучок света падает под углом Брюстера εB. Закон Брюстера: 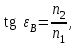 откуда 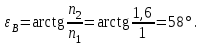 Угол θ между отраженным и падающим пучками света 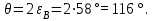 |
| Найти: θ ― ? |
Ответ: θ = 116°.
6.Определить силу тока, протекающего по молибденовой проволоке диаметром d = 1 мм, температура которой в вакууме поддерживается равной Т = 1200°С. Поверхность проволоки принять равной серой с поглощательной способностью a = 0,42. Удельное сопротивление проволоки ρ = 0,37 мкОм*м.
| Дано: d = 1 мм = 1∙10-3 м Т = 12000С = 1473 К a = 0,42 T0 = 00С = 273 К ρ = 3,7∙10-4 Ом∙м | Решение: Мощность постоянного тока 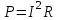 где I – сила тока, R –сопротивление проволоки. Сопротивление проволоки зависит от природы проводника, его геометрических размеров 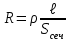 , ,где Sсеч – площадь поперечного сечения проводника, равная 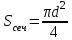 Таким образом, мощность тока равна 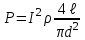 (1) (1)В то же время, подводимая мощность будет равна разности излучаемой Pизл и поглощаемой Рпогл мощностей: 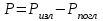 Излучаемая мощность Ризл равна 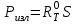 Согласно закону Стефана-Больцмана, энергетическая светимость пропорциональна абсолютной температуре Т тела в четвертой степени: 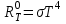 Тогда излучаемая мощность 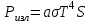 где 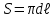 площадь поверхности проволоки. Поглощаемая мощность будет определяться похожим выражением: площадь поверхности проволоки. Поглощаемая мощность будет определяться похожим выражением: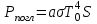 Тогда подводимая мощность: 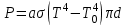 (2) (2)Приравняв выражения (1) и (2) и выразив из получившегося равенства силу тока, найдем 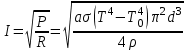 где 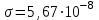 Вт/(м2∙К4) – постоянная Стефана-Больцмана. Вт/(м2∙К4) – постоянная Стефана-Больцмана.Вычисляем:  |
| Найти: I - ? |
Ответ:
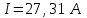 .
.7.Определить красную границу фотоэффекта, если работа выхода электронов из фотокатода А = 2,15 эВ.
| Дано: А = 2,15 эВ = 3,44*10-19 Дж λ0 = 275 нм = 275∙10–9 м | Решение: 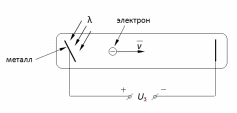 Покажем рисунок. Энергия падающего фотона 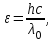 где h — постоянная Планка; c — скорость света в вакууме; λ0 — длина волны. Формула Эйнштейна для фотоэффекта: 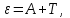 где A — работа выхода из металла; T — максимальная кинетическая энергия фотоэлектронов. Поскольку λ0 ― красная граница фотоэффекта, то кинетическая энергия электрона T = 0, вся энергия ε фотона идет на работу выхода A: 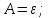 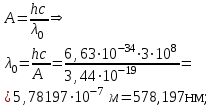 |
| Найти: λ0 ― ? |
Ответ:
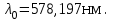
8.При каком значении кинетической энергии (в эВ) длина волны де Бройля λ электрона равна его комптоновской длине волны λc?
| Дано: Электрон λ = λБ = λс = λК | Решение: Длина волны де Бройля 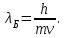 Длина волны Комптона 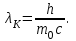 По условию 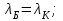 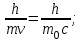 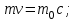 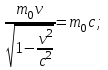 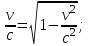 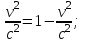 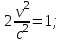 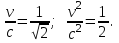 Кинетическая энергия электрона: 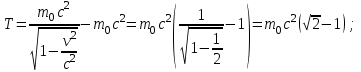 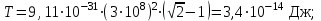 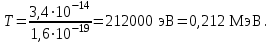 |
| Найти: T ― ? |