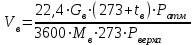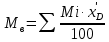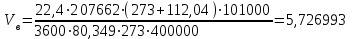Файл: Федеральное государственное бюджетное образовательное учереждение высшего образования тюменский индустриальный университет.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 216
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Искомая величина е`=0,0916.
Молекулярные веса компонентов Mi вычисляем по формуле Воинова. По данным таблицы 10 средний молекулярный вес нефти:
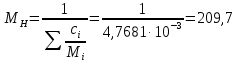
Молекулярный вес паровой фазы:
My=
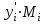 =100,985
=100,985Массовая доля отгона:
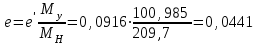
2.8 Минимальное флегмовое число
Минимальное флегмовое число Rmin определяется по уравнениям Андервуда:
лонна нефть тарелка
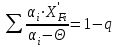
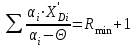
где αi – коэффициент относительной летучести по отношению к ключевому компоненту
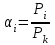
где Pi - давление насыщенных паров при температуре ввода сырья;
Pk – давление насыщенных паров ключевого компонента (давление 3 фракции = 1486,7кПа);
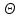 - корень уравнения Андервуда. Обычно его величина находится между значениями i ключевых компонентов. В общем случае при увеличении
- корень уравнения Андервуда. Обычно его величина находится между значениями i ключевых компонентов. В общем случае при увеличении 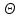 левая часть уравнения возрастает.
левая часть уравнения возрастает.q – отношение количества тепла Q, которое надо сообщить сырью, чтобы перевести его в парообразное состояние, к скрытой теплоте испарения сырья Qисп:
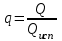 или
или 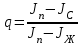
где JC – энтальпия сырья при температуре ввода;
JП – энтальпия насыщенных паров сырья;
JЖ – энтальпия кипящей жидкости сырья.
При расчёте минимального флегмового числа возможны следующие варианты:
а) Если сырьё вводится при температуре кипения, то e`=0 и q=1.
б) Если сырьё вводится в виде холодной жидкости, не доведенной до температуры кипения, то q>1.
в) Если сырьё вводится в виде насыщенных паров, то e`=1 и q=0.
г) Если сырьё вводится в виде перегретых паров
, то q<0.
д) Если сырьё вводится в виде парожидкостной смеси,
то 0
В нашем случае 1-q=e`=0,0916. Методом подбора находим из первого уравнения Андервуда корень
 , подставляем его во второе уравнение и определяем Rmin. Результаты расчета приведены в Таблице 11.
, подставляем его во второе уравнение и определяем Rmin. Результаты расчета приведены в Таблице 11.Расчет выполняется с помощью программы MicrosoftExcel.
Таблица 2.12–Расчёт минимального флегмового числа
| № компо- нента | 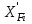 | Piпри tF | i | 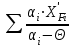 | 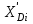 | 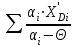 |
| 1 | 0,0562 | 2,8805 | 1,938425 | 0,122963 | 0,48692 | 0,975135 |
| 2 | 0,0512 | 1,8993 | 1,278129 | 0,233914 | 0,44644 | 1,854856 |
| 3 | 0,0446 | 1,4866 | 1,000404 | 0,281014 | 0,05662 | 1,894171 |
| 4 | 0,0575 | 1,2665 | 0,852288 | -0,30858 | 0,01002 | -0,07224 |
| 5 | 0,1404 | 0,7787 | 0,524024 | -0,16842 | 0 | 0 |
| 6 | 0,1301 | 0,3650 | 0,245626 | -0,05527 | 0 | 0 |
| 7 | 0,1611 | 0,1266 | 0,085195 | -0,01175 | 0 | 0 |
| 8 | 0,1944 | 0,0176 | 0,011844 | -0,00184 | 0 | 0 |
| 9 | 0,1645 | 0,0032 | 0,002153 | -0,00056 | 0 | 0 |
| Сумма | 1,0000 | - | - | 0,0916 | 1,0000 | 4,65192 |
Корень уравнения Андервуда равен:
 =0,9705
=0,9705Минимальное флегмовое число равно:
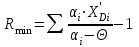 =4,65192-1=3,65192
=4,65192-1=3,651922.9 Оптимальное флегмовое число. Оптимальное число теоретических тарелок
Приведём два способа расчёта оптимального флегмового числа.
Графический способ Джиллиленда
а) Задаёмся коэффициентом избытка флегмы
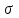 i=(1,1…1,8).
i=(1,1…1,8).б) Рассчитываем флегмовые числа:
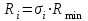
Например,
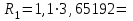 4,0171.
4,0171.в) Находим параметр Хi:
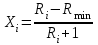
Например,
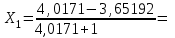 0,0728
0,0728г) Находим параметр Yi:
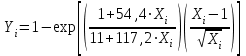
Например,
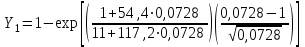 =0,58219
=0,58219д) Находим число теоретических тарелок N из уравнения:
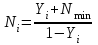
Например,
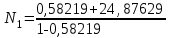 = 60,93338
= 60,93338e) Находим величину Ni(Ri+1).
Например, N1(R1+1)= 60,93338·(4,0171+1)=305,7096
Расчёты приведены в таблице 12.
Таблица 2. 12 –Расчёт параметров Rопт и Nопт
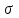 i i | Ri | xi | yi | Ni | Ni(Ri+1) |
| 1,1 | 4,01711 | 0,07279 | 0,58219 | 60,93338 | 305,70961 |
| 1,2 | 4,38230 | 0,13570 | 0,51856 | 52,74824 | 283,90704 |
| 1,3 | 4,74750 | 0,19062 | 0,46857 | 47,69202 | 274,10972 |
| 1,4 | 5,11269 | 0,23897 | 0,42807 | 44,24376 | 270,44833 |
| 1,5 | 5,47788 | 0,28188 | 0,39451 | 41,73605 | 270,36111 |
| 1,6 | 5,84307 | 0,32020 | 0,36617 | 39,82553 | 272,52897 |
| 1,7 | 6,20826 | 0,35464 | 0,34188 | 38,31834 | 276,20872 |
| 1,8 | 6,57346 | 0,38576 | 0,32078 | 37,09683 | 280,95122 |
ж) Строим график Ni(Ri+1)=f(Ri):
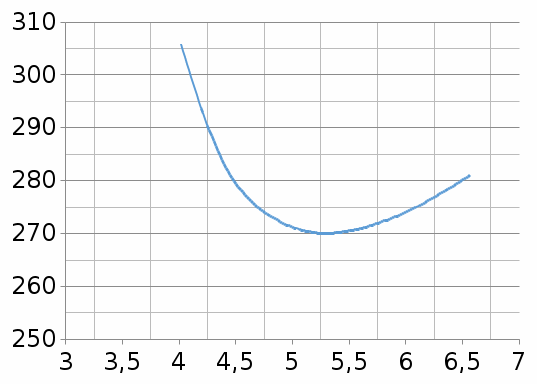
График 1 - Зависимости параметра Ni(Ri+1) от флегмового числа.
Минимум на полученной кривой соответствует искомым параметрам: Rопт=5,30; Nопт=41,73;
 опт=1,5.
опт=1,5.Аналитический вариант расчёта (по приближённым уравнениям):
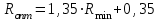
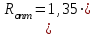 3,65192+0,35=5,2801
3,65192+0,35=5,2801Nопт=1,7
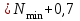
Nопт=1,7·
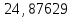 +0,7=42,99
+0,7=42,99Таким образом, оба способа дают довольно близкие результаты. Принимаем к дальнейшим расчётам данные более точного графического способа.1>
2.10 Место ввода сырья в колонну. Рабочее число тарелок
Определяем минимальное число теоретических тарелок в концентрационной части колонны (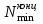 )
)
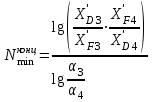 ,
,
где α3 и α4 – коэффициенты относительной летучести компонентов при температуре ввода сырья (Таблица 2.12).
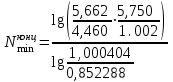 =12,4
=12,4
13
Оптимальное число теоретических тарелок в верхней части колонны
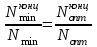
Отсюда 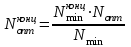
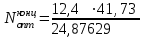 =20,80
=20,80
21
Рабочее число тарелок в колонне:
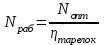
где 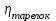 - к.п.д. тарелки, примем равным 0,6.
- к.п.д. тарелки, примем равным 0,6.
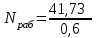 =69,55
=69,55
70
Рабочее число тарелок в верхней части колонны
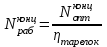
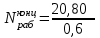 =34,67
=34,67
35
2.10 Место ввода сырья в колонну. Рабочее число тарелок
Определяем минимальное число теоретических тарелок в концентрационной части колонны (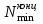 )
)
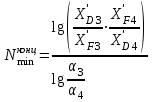 ,
,
где α3 и α4 – коэффициенты относительной летучести компонентов при температуре ввода сырья (Таблица 2.12).
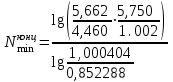 =12,4
=12,4
13
Оптимальное число теоретических тарелок в верхней части колонны
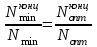
Отсюда 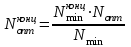
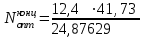 =20,80
=20,80
212.10 Место ввода сырья в колонну. Рабочее число тарелок
Определяем минимальное число теоретических тарелок в концентрационной части колонны (
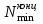 )
)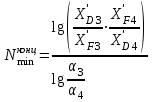 ,
,где α3 и α4 – коэффициенты относительной летучести компонентов при температуре ввода сырья (Таблица 2.12).
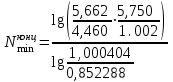 =12,4
=12,4 Рабочее число тарелок в колонне:
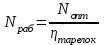
где
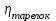 - к.п.д. тарелки, примем равным 0,6.
- к.п.д. тарелки, примем равным 0,6.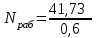 =69,55
=69,55 В нижней, исчерпывающей части колонны, таким образом, будет 70-35=35 тарелок. На практике для ввода сырья предусматривают до 5 точек вблизи сечения, определённого по этим уравнениям.
2.11 Внутренние материальные потоки
а) Верхняя часть колонны.
Количество флегмы, стекающей с тарелок верхней части колонны:
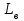 =Rопт·D= 5,2801·33066,60855=174595 кг/ч
=Rопт·D= 5,2801·33066,60855=174595 кг/чКоличество паров, поднимающихся с тарелок верхней части колонны:
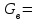
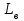 +D=174595+33066,60855=207662 кг/ч
+D=174595+33066,60855=207662 кг/чОбъём паров: