Файл: Учебнике Физика 10 класс.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 08.11.2023

Просмотров: 39

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

«Тайна Броуновского движения» или новые приключения

«Аристотелевой мухи» в учебнике «Физика 10 класс».

«У сложной теории над истинной простотой

есть одно большое преимущество

- она выглядит научно;

а у новой истины есть один огромный недостаток

- она оскорбительно проста для разума любого учёного,

считающего себя умным». 

(В. Бабинцев)
В предыдущей статье - «Тайна «броуновского движения» или приключения "Аристотелевой мухи"» нам вполне хватило знаний 7-9 классов, чтобы показать несостоятельность «Теории броуновского движения» изложенную в новых вариантах издания учебника физики Перышкина для 7 классов основной школы. [1]
Посмотрим теперь, как его трактуют более солидные учебники, для старших классов, есть ли там какие-либо отличия. Возьмем основной, имеющий множество положительных экспертных заключений, соответствующий ФГОС и рекомендованный Министерством образования и науки РФ, учебник «Физика 10 класс, авторы Г.Я. Мякишев, Б.Б. Буховцев и Н.Н. Сотский, Москва, «Просвещение» 2018 г. Далее, все ниже приведённое из учебника будет выделено наклонным шрифтом.

  • Глава 8. Основы молекулярно-кинетической теории. § 55. Броуновское движение.

  • «Самое очевидное доказательство движения молекул можно получить, наблюдая в микроскоп мельчайшие, взвешенные в воде частицы какого-либо твёрдого вещества. Эти частицы совершают беспорядочное движение, которое называют броуновским.

  • Запомни. Броуновское движение — это тепловое движение взвешенных в жидкости (или газе) частиц.

  • Важно. Броуновское движение — тепловое движение, и оно не может прекратиться. С увеличением температуры интенсивность его растёт».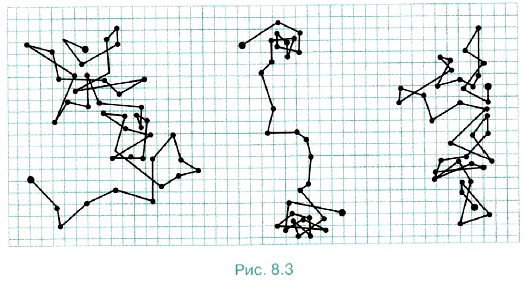

  • На рисунке 8.3 приведены траектории движения броуновских частиц. Положения частиц, отмеченные точками, определены через равные промежутки времени — 30 с. Эти точки соединены прямыми линиями. В действительности траектория частиц гораздо сложнее.

  • Объяснить броуновское движение можно только на основе молекулярно-кинетической теории.

  • Важно. Причина броуновского движения частицы заключается в том, что удары молекул жидкости о частицу не компенсируют друг друга». [2]

« На рисунке 8.4 схематически показано положение одной броуновской частицы и ближайших к ней молекул. При беспорядочном движении молекул передаваемые ими броуновской частице импульсы, например, слева и справа, неодинаковы. Поэтому отлична от нуля результирующая сила давления молекул жидкости на броуновскую частицу. Эта сила и вызывает изменение движения частицы. [2]

Молекулярно-кинетическая теория броуновского движения была создана в 1905 г. А. Эйнштейном (1879—1955). Построение теории броуновского движения и её экспериментальное подтверждение французским физиком Ж. Перреном окончательно завершили победу молекулярно-кинетической теории. В 1926 г. Ж. Перрен получил Нобелевскую премию за исследование структуры вещества. [2]
Вот и все научное объяснение теории броуновского движения для учеников старшей школы (10 класса), основанное на первом научном труде А. Эйнштейна «О движении взвешенных в покоящейся жидкости частиц, требующем молекулярно-кинетической теории теплоты», опубликованном им в 1905 г., положения которого были «подтверждены» в 1909 г. опытами Ж. Перрена.
Посмотрим, хватит ли нам школьных знаний в объеме тех же 9 классов и чуточки Интернета, чтобы разобраться в изложенной сути броуновского движения, приведённой в данном учебнике. Итак, начнем:


  1. Утверждение первое - «Самое очевидное доказательство движения молекул можно получить, наблюдая в микроскоп мельчайшие, взвешенные в воде частицы какого-либо твёрдого вещества». - Бездоказательное (и в корне неверное, что и покажем далее), поскольку о наличии атомов (или молекул) из которых состоят вещества и их подвижности было известно еще со времен Демокрита (если не раньше), всем, кого это как-то интересовало. Впрочем, некоторые маститые ученые и в XIX веке выражали сомнения в их существовании, предлагая иные формулировки и модели строения вещества, отпавшие по пути становления истины.

  2. Утверждение второе - «Запомни. Броуновское движение — это тепловое движение взвешенных в жидкости (или газе) частиц». - Голословное, ибо не сопровождается никакими доказательствами. Добавим, что при отсутствии внешних воздействий, в состоянии термодинамического равновесия, молекулы жидкостей в отличии от молекул газов, практически неподвижны. Простейшим доказательством этому служат опыты по прогреву столба воды со стороны ее поверхности или опыты с ее переохлаждением. [3]

  3. Утверждение третье - «Важно. Броуновское движение — тепловое движение, и оно не

может прекратиться». - Такое же голословное, фактически вытекающее из предыдущего.

  1. Утверждение четвертое - «С увеличением температуры интенсивность его (броуновского движения) растёт». - Что значит интенсивность? Скорость движения или частота смены направления движения частиц? Это тянет на «Открытие Америки». С времен Древнего мира известно, что с увеличением температуры уменьшается вязкость жидкостей и газов (особенно наглядно это видно на примере «густых» жидкостей, смолы, меда, дегтя, мазута и т.д.), и, следовательно, уменьшается сопротивление движению находящихся в них тел. [3]

  2. Утверждение пятое - «На рисунке 8.3 приведены траектории движения броуновских частиц. Положения частиц, отмеченные точками, определёнными через равные промежутки времени — 30 с. Эти точки соединены прямыми линиями. В действительности траектория частиц гораздо сложнее». – Предоставлены копии зарисовок движения отдельных частиц с опытов Перрена, ничего в сущности не объясняющие. Приглядимся внимательно к траекториям броуновских частиц, приведенных на рис.8.3. Видно, что они, двигаясь, казалось бы, хаотически, в целом перемещаются в одну сторону, значит есть какая-то сила заставляющая их в итоге двигаться в одном направлении. Что это за сила, узнаем далее.

  3. Утверждение шестое. «На рисунке 8.4 схематически показано положение одной броуновской частицы и ближайших к ней молекул ...».

6.1. Мы уже разбирали этот казус в предыдущей статье [1]. Тем не менее, еще раз отметим, что приведенная на рис.8.4 схематическая модель броуновского движения никак не отображает реалии. Изображенная на нем броуновская частица в размерах превышает молекулы всего в 10 раз! Кроме этого, между молекулами наличествуют большие промежутки, «как в газах», что так же не соответствует канве рассуждений об опытах в жидкостях. [1]

6.2. Для примера сравним реальные размеры молекулы воды и стандартной броуновской частицы.

Молекула воды имеет диаметр примерно Dм=2Rм=3·10-10 м (3·10-4мкм). Размеры частиц, подчиняющихся эффекту Броуна в диаметре не более Dбч=2Rбч=3·10-6м (3 мкм). [1], [5]




Отношение их линейных размеров будет отличаться в М=D
бч/Dм=3·10-6/3·10-10=104 или в 10000 раз!

6.3. Жидкости практически не сжимаемы, потому как молекулы в них (в отсутствии турбулентностей) расположены упорядоченно и вплотную друг к другу так, что другой просто некуда втиснуться. Посчитаем примерное количество молекул воды, которые будут первым слоем окружать сферическую броуновскую частицу вдоль всей ее поверхности.[5]

- Площадь поверхности такой броуновской частицы Sбч=4πR2бч=28,26*10-12м2. Площадь радиального сечения молекулы воды Sсм=πRм2=7,1*10-20м2.

- Отсюда броуновскую частицу будет окружать слой примерно из N= Sбч/Sсм=4*108 молекул иначе

400 000 000 шт., за которым вплотную следуют другие слои с еще большим их количеством. [1]

6.4. Если в том же масштабе по отношению к изображенной «броуновской» частице, изобразить голубыми точками молекулы воды, то квинтильоны микроточек молекул сольются в сплошной фон, что и показано на рисунке, приведенном справа от Рис. 8.4., взятого из учебника. [1]

6.5. В принципе, уже этого несоответствия вполне достаточно, чтобы опровергнуть излагаемую «на пальцах» теорию в нашем учебнике, однако далее:


  1. Утверждение седьмое - «Важно. Причина броуновского движения частицы заключается в том, что удары молекул жидкости о частицу не компенсируют друг друга».

7.1. Повторимся, броуновскую частицу в спокойной жидкости окружает плотное структурированное несжимаемое облако молекул, которые никак не шарахаются с газовыми скоростями, а в отсутствии турбулентностей, тихо дрожат около положения равновесия. [3]

7.2. А теперь вопрос. Вы пробовали когда-нибудь разбежаться в плотной стоящей многотысячной толпе, окружающей здоровенный трактор, чтобы со всей дури толкнуть его?

7.3. Напомним, обрести «газовые скорости» молекулы жидкости могут, когда вылетают с ее поверхности под действием внешних воздействий (газовых потоков) или при температуре кипения. [3]

7.4. А вдруг они все-таки двигаются и «удары молекул жидкости о частицу не компенсируют друг друга». Просчитаем и этот фантастический случай:

- Объем молекулы воды, считая ее сферической Vм=14,13*10-30м3, объем соответствующей сферической броуновской частицы будет Vбч= 14,13*10-18м3.

- Отношение их объемов будет соответствовать и примерному отношению их масс, т.е. Z=V
бч/Vм=Мбч/Мм=14,13*10-18/14,13*10-30=1*1012, заметьте, по объему или по массе они разнятся примерно в 1000 000 000 000 раз. [1]

7.5. Не надо быть физиком, чтобы понять, что сдвинуть с места броуновскую частицу в плотной «толпе» других молекул ее окружающих (разве что на ничтожнейшую величину в вакууме) не сможет ни одна «сверхсуперсильная» молекула не только в жидкостях, но и в газах.

7.6. Отметим, для заметного в микроскоп сдвига броуновской частицы нужен импульс (синхронный удар) армии молекул соизмеримой с броуновской частицей по массе, хотя бы от 1010-1012 молекул, собранных в мощный кулак. И это при условии, что другие армии молекул (от 1010-1012 шт.) окружающие частицу будут совершать синхронные перемещения, дабы не противодействовать этой ударной группировке. [1] Наверное, тот можно было бы остановиться во второй раз, однако продолжим…


  1. Утверждение восьмое - «Объяснить броуновское движение можно только на основе молекулярно-кинетической теории» - опять голословное, ибо оного в учебнике просто нет. Вследствие его отсутствия попробуем с позиции МКТ дать его мы.

8.1. Итак, в жидкостях броуновская частица окружена плотным не сжимаемым «облаком» молекул, которые, в отличии от газов, не носятся хаотично, а в отсутствии конвекционных потоков флуктуируют (дрожат) каждая около своего положения равновесия. Простейшим доказательством этого являются опыты по сжиманию воды и попытки ее «кипячения» со стороны поверхности. [3]

8.2. Согласно МКТ направления и скорости движения молекул в газах и дрожания молекул в жидкостях носят равновероятностный характер, и, следовательно, суммарный вектор разнонаправленных импульсов несметного числа молекул окружающих броуновскую частицу будет равен НУЛЮ 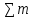i*vi=0, как говорится «без комментариев».[2]


  1. Тут можно было бы в третий раз вытереть пот со лба, но в учебнике «вишенкой на торте» лежит пересказ опытов физика Ж. Перрена проделанных им в 1909 г. и получившим в 1926 г. Нобелевскую премию «за экспериментальное доказательство» правильности теории «броуновского движения» А. Эйнштейна.




  • Опыты Перрена (пересказ учебника).  Идея опытов Перрена состоит в следующем. Известно, что концентрация молекул газа в атмосфере уменьшается с высотой. Если бы не было теплового движения, то все молекулы упали бы на Землю и атмосфера исчезла бы. Однако если бы не было притяжения к Земле, то за счёт теплового движения молекулы покидали бы Землю, так как газ способен к неограниченному расширению. В результате действия этих противоположных факторов устанавливается определённое распределение молекул по высоте, т. е. концентрация молекул довольно быстро уменьшается с высотой. Причём чем больше масса молекул, тем быстрее с высотой убывает их концентрация. [2]

  • Броуновские частицы участвуют в тепловом движении. Так как их взаимодействие

Смотрите также файлы