Файл: Кинематическая схема машинного агрегата.doc

Недогрузка допустимо 10%.

Расчетные напряжения изгиба

σ_F2 = Y_F2Y_βF_tK_FαK_FβK_Fv/(mb₂),

где Y_F2 – коэффициент формы зуба,

Y_β = 1 – β/140 = 1 – 9,01/140 = 0,936

K_Fα = 0,91 – для косозубых колес,

K_Fβ = 1 – для прирабатывающихся зубьев

K_Fv = 1,05 – коэффициент динамической нагрузки [1c.64].

Коэффициент формы зуба:

при z₁ = 28 → z_v1 = z₁/(cosβ)³ = 28/0,9900³ = 29 → Y_F1 = 3,805

при z₂ = 137 → z_v2 = z₂/(cosβ)³ =137/0,9900³ = 141 → Y_F2 = 3,61

σ_F2 = 3,61·0,936·1603·0,91·1,0·1,05/(1,5·50) = 69,0 МПа < [σ]_F2

σ_F1 = σ_F2Y_F1/Y_F2 = 69,0·3,805/3,61 = 72,7 МПа < [σ]_F1.

Так как расчетные напряжения σ_H < [σ_H] и σ_F < [σ]_F, то можно утверждать, что данная передача выдержит передаваемую нагрузку и будет стабильно работать в нормальных условиях весь срок службы.

5. Расчет и проектирование клиноременной передачи открытого типа /1 с.82/

Выбор ремня

По номограмме [1c83] выбираем ремень сечения А

Диаметры шкивов

Минимальный диаметр малого шкива d_1min = 90 мм [1c84]

Принимаем диаметр малого шкива на 1…2 размера больше

d₁ = 100 мм

Диаметр большого шкива

d₂ = d₁u(1 – ε) = 100∙2,21(1 - 0,01 ) = 219 мм

где ε = 0,01 – коэффициент проскальзывания

принимаем d₂ = 224 мм

Межосевое расстояние

a > 0,55(d₁+d₂) + h = 0,55(100+224) + 8,7 = 187 мм

h = 8,7 мм – высота ремня сечением А

принимаем а = 200 мм

Длина ремня

L = 2a + w +y/(4a)

w = 0,5π(d₁+d₂) = 0,5π(100+224) = 509

y = (d₂ - d₁)² = (224 – 100)² = 15376

L = 2∙200 + 509 +15376/(4∙200) = 928 мм

принимаем L = 900 мм

Уточняем межосевое расстояние

a = 0,25{(L – w) + [(L – w)² – 2y]^0,5} =

= 0,25{(900 – 509) +[(900 – 509)² - 2∙15376]^0,5} = 185 мм

Угол обхвата малого шкива

α₁ = 180 – 57(d₂ – d₁)/a = 180 – 57(224-100)/185 = 142º

Скорость ремня



Окружная сила

---

Допускаемая мощность передаваемая одним ремнем



Коэффициенты:

C_p = 1,0 – спокойная нагрузка

C_α = 0,91 – при α₁ = 142º

C_l = 0,975 – коэффициент влияния длины ремня

С_z = 0,95 – при ожидаемом числе ремней 4÷5

P₀ = 0,95 кВт – номинальная мощность передаваемая одним ремнем



Число ремней

z = Р/[Р] =1,59/0,8 = 1,98

принимаем z = 2

Натяжение ветви ремня



Сила действующая на вал



Прочность ремня по максимальным напряжениям в сечении ведущей ветви ремня

σ_max = σ₁ + σ_и+ σ_v < [σ]_p = 10 Н/мм²

σ₁ – напряжение растяжения



А = 81 мм² – площадь сечения ремня
σ_и – напряжение изгиба

σ_и = E_иh/d₁ = 80∙8/100 = 6,4 Н/мм²

E_и = 80 Н/мм² – модуль упругости

– напряжение от центробежных сил

σ_v = ρv²10^-6 = 1300∙5²∙10^-6 = 0,03 Н/мм²

ρ = 1300 кг/м³ – плотность ремня

σ_max = 2,77+6,4+0,03 = 9,2 Н/мм²

- для клиновых и поликлиновых ременй

условие σ_max < [σ]_p выполняется

6 Нагрузки валов редуктора

Силы действующие в зацеплении цилиндрической косозубой передачи

окружная

F_t = 1603 Н

радиальная

F_r = 526 H

осевая

F_a = 228 H

Консольная сила от клиноременной передачи действующая на быстроходный вал

F_в = 696 Н

Горизонтальная и вертикальная составляющие консольной силы от ременной передачи, действующие на вал

---

Консольная сила от муфты действующая на тихоходный вал





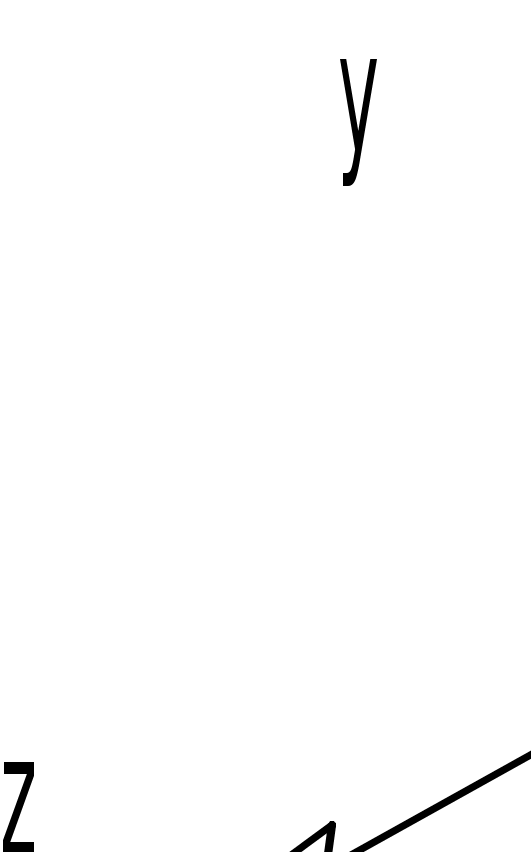
Рис. 6.1 – Схема нагружения валов цилиндрического редуктора с наклонным разъемом корпуса

7. Разработка чертежа общего вида редуктора.

Материал быстроходного вала – сталь 45,

термообработка – улучшение: σ_в = 780 МПа;

Допускаемое напряжение на кручение [τ]_к = 10÷20 Мпа
Диаметр быстроходного вала



где – передаваемый момент;

принимаем диаметр выходного конца d₁ = 25 мм;

длина выходного конца:

l₁ = (1,01,5)d₁ = (1,01,5)25 = 2538 мм,

принимаем l₁ = 35 мм.

Диаметр вала под уплотнением:

d₂ = d₁+2t = 25+22,2 = 29,4 мм,

где t = 2,2 мм – высота буртика;

принимаем d₂ = 30 мм:

длина вала под уплотнением:

l₂  1,5d₂ =1,530 = 45 мм.

Диаметр вала под подшипник:

d₄ = d₂ = 30 мм.

Вал выполнен заодно с шестерней
Диаметр выходного конца тихоходного вала:



принимаем диаметр выходного конца d₁ = 35 мм;

длина выходного конца:

l₁ = (1,52,0)d₁ = (1,52,0)35 = 52,570 мм,

принимаем l₁ = 60 мм

Диаметр вала под уплотнением:

d₂ = d₁+2t = 35+22,8 = 40,6 мм,

где t = 2,8 мм – высота буртика;

принимаем d₂ = 40 мм .

Длина вала под уплотнением:

l₂  1,25d₂ =1,2540 = 50 мм.

Диаметр вала под подшипник:

d₄ = d₂ = 40 мм.

Диаметр вала под колесом:

d₃ = d₂ + 3,2r = 40+3,23,0 = 49,6 мм,

принимаем d₃ = 50 мм.
Выбор подшипников

---

Предварительно назначаем радиальные шарикоподшипники легкой серии №206 для быстроходного вала и №208 для тихоходного вала.

Условное обозначение подшипника	d мм	D мм	B мм	С кН	С0 кН
№206	30	62	16	19,5	10,0
№208	40	80	18	32,0	17,8

7. Расчетная схема валов редуктора

   1. Быстроходный вал

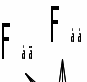
Рис. 8.1 – Схема нагружения быстроходного вала
Горизонтальная плоскость.

Сумма моментов сил и реакций опор относительно опоры А

m_A = 57F_t – 114B_X + 77F_вг = 0

Отсюда находим реакцию опоры В в плоскости XOZ
B_X = (57F_t +77F_вг )/114 = (57·1603+77·162)/114 = 911 H

Сумма моментов сил и реакций опор относительно опоры В

m_В = 57F_t – 114А_X –191F_вг = 0
Отсюда находим реакцию опоры А в плоскости XOZ

А_X = (57F_t – 191F_вг )/114 = (57·1603 – 191·162)/114 = 530 H

Изгибающие моменты в плоскости XOZ

M_X1 =911·57 = 51,9 Н·м

M_X1 = 530·77 = 40,8 Н·м

Проверка

А_Х – F_t +B_X + F_вг = 530 – 1603 +911+162 = 0

Вертикальная плоскость.

Сумма моментов сил и реакций опор относительно опоры А

m_A = 57F_r + 114B_Y – F_a1d₁/2 – 77F_вв = 0

Отсюда находим реакцию опор В в плоскости YOZ

B_Y =(–57 F_r+F_a1d₁/2+77F_вв)/114= (–57·526+228·42,42/2+77·677)/114=237 H

Сумма моментов сил и реакций опор относительно опоры B

m_В = 57F_r – 114A_Y + F_a1d₁/2 + 191F_вв = 0

Отсюда находим реакцию опор A в плоскости YOZ

A_Y = (57·526 +228·42,42/2 + 191·677)/114 = 1440 H

Проверка

F_вв + B_Y + F_r – A_Y = 677+237+526 – 1440 = 0

Изгибающие моменты в плоскости YOZ

M_Y = 71·57 = 4,0 Н·м

M_Y = 677·77 = 51,1 Н·м

M_Y = 677·134 – 1440·57 = 8,6 Н·м

Суммарные реакции опор:

А = (А_Х² + А_Y²)^0,5

---

= (530² +1440²)^0,5 =1534 H

B= (B_Х² + B_Y²)^0,5 = (911² + 237²)^0,5 =941 H

8.2 Тихоходный вал

Рис. 8.2 – Схема нагружения тихоходного вала.

Горизонтальная плоскость. Сумма моментов сил и реакций опор относительно опоры С

m_С = 58F_t + 116D_X – 224F_м = 0

Отсюда находим реакцию опоры D в плоскости XOZ

D_X = (224·1603 – 58·1603)/116 = 2294 H
Реакция опоры С в плоскости XOZ

C_X = D_X + F_t– F_м = 2294+1603 – 1603 = 2294 H

Изгибающие моменты в плоскости XOZ

M_X1 =2294·58 =133 Н·м

M_X2 =1603·108 =173 Н·м

Проверка

С_Х – F_t – D_X + F_м = 2294 – 1603 – 2294 +1603 = 0

Вертикальная плоскость. Сумма моментов сил и реакций опор относительно опоры С

m_С = 58F_r+ F_ad₂/2 – 116D_Y = 0

Отсюда находим реакцию опоры C и D в плоскости XOZ

D_Y = (58·526+228·207,58/2)/116 = 467 H

C_Y = F_r – D_Y = 526 – 467 = 59 H

Изгибающие моменты в плоскости XOZ

M_X1 = 59·58 = 3,4 Н·м

M_X2 = 467·58 = 27,1 Н·м

Проверка

С_Y – F_r + D_Y = 59 – 526 + 467 = 0
Суммарные реакции опор:

C = (2294² + 59²)^0,5 =2295 H

D = (2294² +467²)^0,5 = 2341 H

7. Проверочный расчет подшипников

9.1 Быстроходный вал

Отношение F_a/C_o = 228/10,010³ = 0,0228  е = 0,21 [1c. 143]

Проверяем наиболее нагруженный подшипник А.

Отношение F_a/А =228/1534 = 0,15 < e, следовательно Х=1,0; Y= 0

Эквивалентная нагрузка

P = (XVF_r + YF_a)K_бК_Т

где Х – коэффициент радиальной нагрузки;

V = 1 – вращается внутреннее кольцо;

F_r – радиальная нагрузка;

Y – коэффициент осевой нагрузки;

K_б =1,3– коэффициент безопасности при нагрузке с умеренными толчками ;

К_Т = 1 – температурный коэффициент.



Требуемая грузоподъемность подшипника

С_тр = Р(573ωL/10⁶)^1/m,

где m = 3,0 – для шариковых подшипников

---