ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.11.2023
Просмотров: 29
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
В Западной Европе практически не пользовались счетами, они встречались там только как наглядное пособие в школах. Прообразом современных счетов явился так называемый дощаный счёт, возникший впервые в России в 16 веке. Большое влияние на создание дощаного счёта оказала система налогового обложения в России 15—17 вв. (сошное письмо), при которой, наряду со сложением, вычитанием, умножением и делением целых чисел, надо было производить те же операции и с дробями, поскольку условная единица обложения — соха, делилась на части. Дощаный счёт представлял собой два складывающихся ящика.
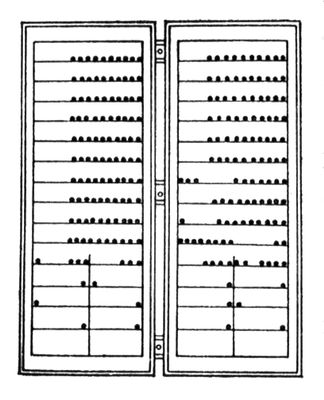Каждый ящик разгораживался надвое (позже только внизу); второй ящик был необходим ввиду особенностей денежного счёта. Внутри ящика на натянутые шнуры или проволоку нанизывались кости. В соответствии с десятичной системой счисления ряды для целых чисел имели по 9 или 10 костей; операции с дробями производились на неполных рядах: ряд из трёх костей составлял три трети, ряд из четырёх костей — четыре четверти (чети). Ниже располагались ряды, в которых было по одной кости: каждая кость представляла половину от той дроби, под которой она располагалась (например, кость, расположенная под рядом из трех костей, составляла половину от одной трети, кость под ней — половину от половины одной трети, и т. д.). Дроби суммировались без приведения к общему знаменателю, например «четь да полтрети, да полполчети»: 
. Иногда операции с дробями производились как с целыми при помощи приравнивания целого (сохи) к определённой сумме денег. Например, при равенстве соха = 48 денежным единицам приведённая выше дробь составит 12 + 8 + 3 = 23 денежные единицы. На рисунке - слева отложена сумма дробей
, а справа 30 рублей 18 алтын 
деньги.С переходом к арабским цифрам и отменой сошного письма счеты утратили в конце 17 века ряды для дробей, а в начале 18 века лишились второго ящика и приобрели свой современный вид (сохранившийся в счетах один неполный ряд, обычно из четырёх костей, отделяет два ряда для десятых и сотых единицы, а также иногда служит для счёта четвертей и половинок).
Русские математические книги.
Монах Кирик написал в 1134 году книгу «Кирика - диакона Новгородского Антониева монастыря учение, им же ведати человеку числа всех лет». В этой книге Кирик подсчитывает, сколько месяцев, сколько дней, сколько часов он прожил, вычисляет в месяцах, неделях и в днях время, прошедшее до 1134 года от «сотворения мира», выполняет разные вычисления дней церковных праздников на будущее время. При счислении времени Кирик употребляет «дробные часы», подразумевая под ними пятые, двадцать пятые, сто двадцать пятые (и так далее) доли часа.
Далее следует период татаро-монгольского ига, после свержения которого оказалось, что Россия значительно отстала от других европейских стран. Только в XVI веке, при Иване Грозном, на Руси появляются первые рукописные учебники по математике, а немного позже – печатные книги о применении математики для различных практических нужд. Исконно русским руководством, излагавшим приемы измерения площадей, является «Книга сошного письма», самый древний экземпляр которой относится к 1629 году. Имеются ведения, что оригинал был составлен еще раньше, при Иване Грозном в 1556 году.
При вычислении площадей фигур рекомендуется в этой книге разбивать их на квадраты, прямоугольники, треугольники, трапеции. Площади квадрата и прямоугольника вычислялись по применяемым сейчас правилам. Площадь же треугольника находилась как половина произведения основания на боковую сторону. Последнее правило, буквально понятое, неверно, так как оно справедливо лишь для прямоугольного треугольника. Возможно, что русская землемерная практика имела дело только с прямоугольными или почти прямоугольными треугольниками, и в таком случае, мы не имеем основания делать упрек нашим предкам в незнании правил начальной геометрии. В те отдаленные времена земля не являлась предметом купли-продажи, и точность результата измерения играла не значительную роль. Оказывается, что в южнорусских губерниях, где свободной земли было много и она поэтому не ценилась, такие приемы оценки площадей применялись еще в ХIХ веке.
При Иване Грозном было составлено и первое русское руководство по землемерию - книга «... глубокомудрая, дающая легкий способ измерять места самые недоступные, плоскости, дебри». А в середине XVI века была составлена первая общая карта Европейской России, которая вместе с «Чертежами Сибирских земель» 1667 года считается самым замечательным памятником русской картографии. В одной из рукописей XVI века впервые упоминается «премудрый Клидас», то есть основоположник нашей современной геометрии - Евклид.
Ранние русские рукописи содержат и теорему Пифагора. Но в них нет явного указания о том, что теорема имеет место только для прямоугольного треугольника. Возможно, что ею пользовались для приближенного нахождения расстояния и в том случае, когда треугольник почти прямоугольный. В 1625 году была переведена с английского языка книга по геометрии, где дается учение о круге. Эта рукопись представляет, по-видимому, обработку «Начал» Евклида, то есть первую часть нашего обычного школьного учебника геометрии.
В 1703 году Леонтий Филиппович Магницкий опубликовал громадную книгу под длинным названием: «Арифметика, сиречь наука числительная, с разных диалектов на славянский язык переведенная и во едино собрана и на две книги разделена... Сочинися сия книга через труды Леонтия Магницкого».
Книга эта содержит начала математических знаний того времени: арифметики, алгебры, геометрии и тригонометрии. В конце книги имеется снабженный большим числом таблиц отдел, посвященный морскому делу. Большую часть книги, как указывает и ее заглавие, автор посвящает арифметике. Магницкий высоко ценит теорию. Он делит свою «Арифметику» на две книги: первую называет «арифметика-политика», вторую – «арифметика-логистика». Первая назначается для тех, кто желает только научиться решать практические вопросы: «исчисляти всякое исчисление в продаже и куплях». Эта часть изложена без доказательств, рассказом и показом - решением примеров.
Вторая часть – «арифметика-логистика» - решает общие вопросы, «токмо уму нашему подлежащие». Магницкий заявляет, что их решать при помощи простых средств «арифметики-политики» нельзя. Без обоснования правил все последующее построение непрочно и бесполезно и так поступать будет неуместно.
Такую же разъяснительную работу проводит и первый печатный учебник геометрии – «Приемы циркуля и линейки» (1709): «Кто хвалит только теорию, укладывает лишь хорошее основание, на котором он ничего не строит; это подобно пушкам, которые не вывозятся на поле сражения, или кораблям, гниющим в гавани. Такой теоретик подобен ремесленнику, знающему свое дело, но знаний своих не применяющему, инженеру, который строит крепости только на бумаге, корабельщику, ездящему в своем доме по карте в Америку. Не лучше и тот, что одну только практику признает: это человек, строящий крепость на песке, подводящий подкоп под Дунай-реку и думающий на кое-как сколоченном плоту совершить путешествие в Индию».
Книга Евклида впервые в печати на русском языке появилась в 1739 году под заглавием: «Евклидовы элементы в осьмь книг через профессора математики Андрея Фархварсона сокращенные. С латинского на российский язык хирургусом Иваном Сатаровым преложенные. В Санкт-Петербурге, 1739». Продолжением этой книги являлись вышедшие в 1745 году «Архимедовы теоремы» в переводе того же Ивана Сатарова. Через эти книги русскому читателю стало доступным все существенное из классического наследия по элементарной геометрии.
Российские математики.
Дерзайте ныне ободренны
Раченьем вашим показать,
Что может собственных Платонов
И быстрых разумом Невтонов
Российская земля рождать.
М.В. Ломоносов
Одно только перечисление российских математиков займет не одну страницу, но их имена не известны широким кругам нашего общества, потому что они занимались очень сложными математическими вопросами. Откройте Энциклопедический словарь на одну букву «А» и прочитайте, к примеру, всех академиков-математиков по фамилии Александров:
Александров Александр Данилович (1912-99), российский математик, академик РАН (1991; академик АН СССР 1964). В 1952-64 ректор ЛГУ. Основные труды по геометрии и ее приложениям, основаниям теории относительности и философии естествознания. Государственная премия СССР (1942).
Александров Анатолий Петрович (1903-94), российский ученый, академик РАН (1991; академик АН СССР с 1953), президент АН СССР (1975-86), трижды Герой Социалистического Труда (1954, 1960, 1973). Ленинская премия (1959), Государственная премия СССР (1942, 1949, 1951, 1953). Золотая медаль им. И. В. Курчатова (1968), им. М. В. Ломоносова (1978), им С. И. Вавилова (1978) и др.
Александров Павел Сергеевич (1896-1982), российский математик, основатель научной школы по топологии, академик АН СССР (1953), Герой Социалистического Труда (1969). Труды по топологии, теории множеств, теории функций. Государственная премия СССР (1943).
Только ради интереса посмотрим в Энциклопедическом словаре исконно русские фамилии Иванов, Петров и Сидоров.
Иванов Валентин Константинович (1908-92), российский математик, член-корреспондент РАН (1991; член-корреспондент АН СССР с 1970). Труды по теории функций, некорректным задачам математической физики. Ленинская премия (1966).
Иванов Иван Иванович (1862-1939), математик, член-корреспондент АН СССР (1925; член-корреспондент РАН с 1924). Труды по теории чисел.
Петров Александр Александрович (р. 1934), российский ученый в области прикладной математики и информатики, академик РАН (1997; член-корреспондент РАН с 1991). Труды в области математического моделирования сложных систем и методам оценки потенциальных возможностей экономики на основе множества критериев. Государственная премия СССР (1980).
Петров Борис Николаевич (1913-80), российский ученый, академик (1960), вице-президент (с 1979) АН СССР, Герой Социалистического Труда (1969). Труды по теории автоматического регулирования, системам автоматического управления движущимися объектами, самонастраивающимся системам. Ленинская премия (1966), Государственная премия СССР (1972).
Петров Вячеслав Вячеславович (р. 1912), российский ученый, член-корреспондент РАН (1991; член-корреспондент АН СССР с 1972). Основные труды по технической кибернетике, теории автоматического регулирования. Государственная премия СССР (1972).
Сидоров Анатолий Федорович (1933-99), российский математик, академик РАН (1991). Основные труды по аналитичеким методам гидроаэромеханики, численным методам решения задач механики сплошной среды.
И это только мизерная часть огромного отряда высокообразованных российских ученых в области математики.
Разве могла бы наша страна первенствовать в космонавтике, если бы не имела крупнейших ученых мирового уровня С. П. Королева, М. В. Келдыша, А. Н. Колмогорова, А. П. Александрова. Только понять их вклад в науку на уровне теорем, уранений и неравенств сможет не всякий учитель математики, не говоря уже о простых обывателях. Поэтому дальнейший выбор из десятков великих людей тех, о ком здесь написать будет субъективен из-за ограниченных рамок реферата. Только две личности, с русским несгибаемым характером борца.
Россия дала миру не только первую женщину-космонавта, но и первую женщину-математика. Её биография позволяет судить насколько сложно было этого добиться несмотря на природные способности.
К
овалевская Софья Васильевна [3(15).1.1850, Москва, — 29.1(10.2).1891, Стокгольм], русский математик, а также писатель и публицист, первая женщина - член-корреспондент Петербургской АН (1889). Ковалевская получила всестороннее образование и рано обнаружила незаурядные математические способности. С 1866 в Петербурге она брала уроки математики у известного педагога А. Н. Страннолюбского. Доступ женщинам в Петербургский университет в то время был закрыт. В 1868 Ковалевская, чтобы иметь возможность заняться наукой, вступила в фиктивный брак и в 1869 уехала в Гейдельберг, где изучала математику. В 1870 переехала в Берлин, где 4 года работала у Карла Вейерштрасса, согласившегося давать ей частные уроки (в Берлинский университет женщины тоже не допускались). В 1874 на основании трёх работ Ковалевской, Гёттингенский университет заочно присудил ей степень доктора философии. В 1874 вернулась в Россию, однако она не смогла получить место в Петербургском университете. Поэтому почти на 6 лет отошла от научной работы, занялась литературно-публицистической деятельностью, сотрудничая в газетах. В 1880 переехала в Москву, но в университете ей не разрешили сдавать магистерские экзамены. В 1881 снова уехала в Берлин, а затем в Париж, пытаясь получить место профессора на Высших женских курсах во Франции. В ноябре 1883 выехала в Швецию, получив приглашение занять должность приват-доцента в Стокгольмском университете. В 1884 была назначена профессором Стокгольмского университета. В 1888 ею написана работа «Задача о вращении твёрдого тела вокруг неподвижной точки»; за эту работу Парижская академия наук присудила С. В. Ковалевской премию. За вторую работу о вращении твёрдого тела (в следующем году) была присуждена премия Шведской академии наук. Ковалевская - автор повести «Нигилистка» (1884), драмы «Борьба за счастье» (1887), семейной хроники «Воспоминания детства» (1890).