Файл: методика лаб_2.docx

Скачать файл (9,00Мб)

Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 16.11.2021

Просмотров: 87

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

МІНІСТЕРСТВО АГРАРНОЇ ПОЛІТИКИ УКРАЇНИ

ПОЛТАВСЬКА ДЕРЖАВНА АГРАРНА АКАДЕМІЯ

Факультет технології виробництва і

переробки продукції тваринництва

Кафедра розведення і генетики

сільськогосподарських тварин

МЕТОДИЧНІ ВКАЗІВКИ

Для ЛАБОРАТОРНИХ РОБІТ З ДИСЦИПЛІНИ

«МЕТОДИКА ТА ТЕХНОЛОГІЯ ОБРОБКИ

НАУКОВОЇ ІНФОРМАЦІЇ В тваринництві»

Для студентів спеціальності

6.090102 “Технології виробництва і переробки продукції тваринництва”

ПОЛТАВА – 2011

Методичні вказівки та завдання до лабораторних і самостійних робіт призначені для індивідуальної роботи студентів факультету «Технології виробництва і переробки продукції тваринництва» під час вивчення дисципліни «Методика та технологія обробки наукової інформації в тваринництві».

Передбачена можливість самоконтролю під час самостійної роботи.

Методична розробка буде корисною для студентів –заочників для самостійного вивчення алгоритмів, процедур і методів статистичного аналізу науково-дослідної інформації.

Методичні вказівки розробили:

Коротков В.А- доцент кафедри розведення і генетики сільськогосподарських тварин кандидат с. – г. наук

Желізняк І.М. - асистент кафедри розведення і генетики сільськогосподарських тварин

Рецензенти: акад. УААН головний
науковий співробітник
інституту свинарства
ім. ОВ Квасницького Рибалко В. П.

Завідувач кафедри вищої
математики, к. ф.-м. н. доцент Флегантов Л. О.

Схвалено методичною радою факультету ТВППТ

(протокол № від “ ” 2011 р.)

Зміст

Стор.

Вступ 4

Лабораторна робота №1

Вивчення інтерфейсу програмного
пакету STATISTICA 5

Лабораторна робота №2

Первинна статистична обробка дослідних
даних в системі STATISTICA 17

Лабораторна робота №3

Побудова діаграм і графіків у системі STATISTICA 20

Лабораторна робота №4

Порівняння статистичних рядів у системі STATISTICA 29

Лабораторна робота №5

Проведення кореляційного аналізу у системі STATISTICA 35

Лабораторна робота №6

Проведення однофакторного дисперсійного аналізу у системі STATISTICA 40

Лабораторна робота №7

Проведення двофакторного дисперсійного аналізу у системі STATISTICA 55

Лабораторна робота №8

Проведення лінійного регресійного аналізу у системі STATISTICA 53

Лабораторна робота №9

Проведення кластерного аналізу у системі STATISTICA 53

Література 64

Додатки 60

Вступ

Використання сучасної комп’ютерної техніки для математичної обробки результатів дослідів є необхідною складовою будь-якого дослідження. Вимоги до сучасних дипломних робіт, досліджень, публікацій в журналах неодмінно передбачають комп’ютерне опрацювання кількісних показників.

На сьогодні така обробка ведеться за допомогою спеціальних програмних пакетів, які звичайно мають досить широкий набір методів математичної статистики.

Посібник призначений для студентів 1 курсу факультету «Технології виробництва і переробки продукції тваринництва» Полтавської державної аграрної академії. Передбачається виконання лабораторних робіт у програмному пакеті Statistica v. 6.0, який має значні переваги перед іншими пакетами: в нього дуже зручний інтерфейс, графіки і таблиці легко масштабуються під час друку, усі підписи можна виконувати кирилицею, тобто українською або російською мовами. Пакет Statistica v.6.0 відповідає всім міжнародним стандартам відносно статистичної обробки матеріалу.

Вивчення курсу „Методика та технологія обробки наукової інформації в тваринництві" передбачає виконання таких видів робіт:

Підготовка до лабораторної роботи. Виконується самостійно у позааудиторний час до заняття. Студент повинен прочитати та законспектувати у робочий зошит означення, деякі теоретичні відомості, а також послідовність, обчислення тих чи інших статистичних параметрів.
Виконання лабораторної роботи. Виконується під час аудиторного заняття або, якщо студент пропустив заняття, у позааудиторний час. Під час аудиторного заняття студент має можливість звертатися у разі виникнення потреби до викладача за допомогою.
Захист лабораторної роботи. Проводиться після виконання студентом лабораторної роботи. Студент повинен дати правильні відповіді на декілька питань, що стосуються теми лабораторної роботи.

Лабораторна робота №1
Засвоєння інтерфейсу системи STATISTICA

Мета роботи:

Ознайомитися з призначенням, інтерфейсом системи STATISTICA, її структурою, порядком роботи та основними модулями програми. Скласти уявлення про можливості і порядок використання програми для статистичної обробки дослідних даних. Навчитися створювати електронну таблицю, вводити в неї дані і зберігати файл з даними на диску.

Завдання

Ознайомтеся з призначенням, інтерфейсом програми STATISTICA, її структурою, порядком роботи та основними модулями програми.

Хід роботи

Ознайомтеся з порядком роботи у пакеті STATISTICA.

Порядок роботи з пакетом STATISTICA

Створити новий файл - базу даних, які призначені для статистичного аналізу, або відкрити раніше створений файл з даними.
Перейти до одного зі спеціальних модулів системи STATISTICA, що містить необхідні методи аналізу, і вибрати потрібний метод.
У діалоговому вікні обраного методу вказати змінні,які необхідно опрацювати, а також, при необхідності, задати деякі параметри методу.

d) Запустити процедуру статистичної обробки вказаних змінних.

є) Переглянути результати статистичної обробки.

2. Ознайомтеся з інтерфейсом пакету STATISTICA.

Початок роботи з системою STATISTICA

Запустіть програму. Запустити програму можна через Головне меню:

Пycк > Пporpaммы > STATISTICA 6 > STATISTICA

Відкриється вікно програми STATISTICA та файл, який був відкритий останнім.

2. Роздивіться головне меню програми. Деякі його пункти (зокрема, ті, що призначені для створення нових файлів, відкриття вже існуючих, для збереження файлів та деякі інші) аналогічні до тих з якими ви зустрічались при вивченні текстового редактора Word та інших програм Microsoft Office).

Рис. 1. Головне меню програми STATISTICA 6

Створити на диску H свою папку.
Запустіть програму "Statistica": Пуск, Программы, sta_win.
В діалоговому вікні "Statistica Module Switcher" виберіть мoдyль "Basic Statistica" та натисніть мишкою по кнопці "Switcher", натиснути "ОК".

Створити файл на диску С у свою папку: File, New Data. В полі "File name" дати ім´я файлу, в полі "Directories" вказати ім´я своєї папки і натиснути "ОК".

3. Підготувати таблицю до вводу даних:

надати заголовок таблиці: двічі натиснути мишкою на білому полі таблиці під заголовком файла данних;
настроїти розміри таблиці.

4. У пункті меню Статистика міститься список основних модулів, які входять до складу системи STATISTICA.

Основні модулі системи STATISTICA

Основна статистика/Таблиці (Basic Statistics/Tables). Модуль містить засоби розрахунку оглядових статистик (мінімум, максимум, середнє, дисперсія, стандартне відхилення, медіана, квартилі, мода), показників лінійної кореляції і парної регресії та ін.

Непараметричні данні (Nonparametrics/Distrib). Модуль містить набір непараметричних методів статистики, які застосовуються для обробки даних, що не відповідають нормальному статистичному розподілу.

Аналіз варіантів (ANOVA/MANOVA). Містить методи дисперсійного аналізу, який дозволяє проводити всебічну оцінку результатів досліду.

Множинна регресія (Multiple Regression). Допомагає з’ясувати ступінь впливу тих або інших факторів на об´єкт методом покровного багатофакторного аналізу.

Ряди динаміки/ Прогнозування (Time Series/ Forecasting). Для порівняння між собою двох вибірок (незалежних та залежних) у системі STATISTICA.

Кластерний аналіз (Cluster Analysis). Містить методи розбиття подібних за кількісними ознаками об’єктів на групи.

Факторний аналіз (Factor Analysis). Містить методи виявлення факторів, які суттєво впливають на явища або процеси, що спостерігаються.

Data Management/MFM (Керування даними/Менеджер метафайлів).

Дозволяє виконувати операції з файлами і даними: створення нового файлу даних, злиття двох файлів в один, перенос частини даних в інший файл, сортування даних, перевірку значень змінних тощо. А також відкриття існуючого файлу з даними і перетворення файлу даних з формату системи STATISTICA у так званий метафайл.

Файловий сервер системи STATISTICA (STATISTICA File Server). Дозволяє швидко відкривати і редагувати всі типи файлів, які використовує система STATISTICA.

4. Ознайомтеся з порядком створення нової розрахункової таблиці (бази даних) у пакеті STATISTICA.

Створення нової таблиці

4.Аналіз даних у системі STATISTICA розпочинається зі створення бази даних - електронної таблиці, що містить вихідні дані, або з відкриття раніше створеного файлу з даними. Для створення нової таблиці, що містить вихідні дані, або з відкриття раніше створеного файлу з даними. Для створення нової таблиці (яка міститиме 5 стовпчиків та 3 рядки) виконайте команди: Файл > Новый.

Відкриється вікно Create New Document (Створити новий документ) (рис.2).

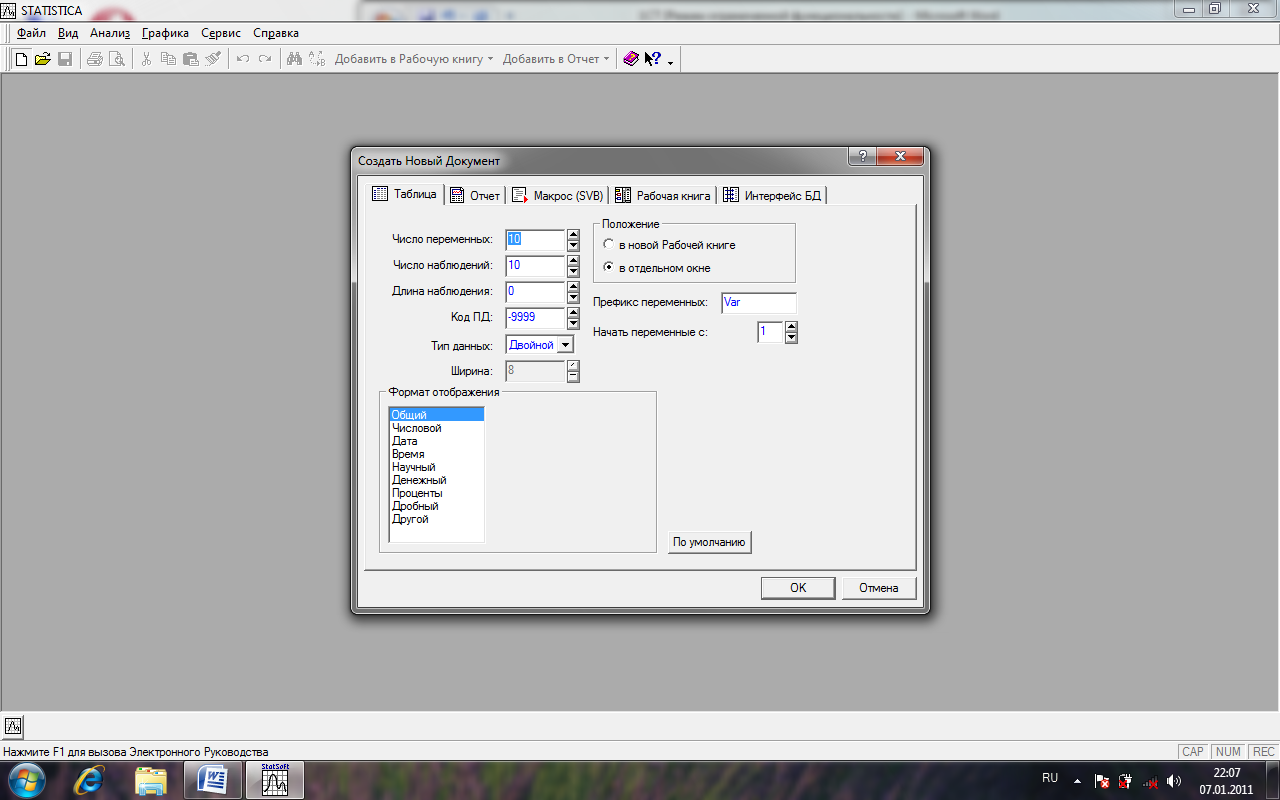
Рис.2. Вікно Create New Document (Створити новий документ)

У цьому вікні треба задати у відповідних полях кількість змінних (кількість стовпців майбутньої таблиці з даними) та кількість регістрів (кількість рядків) нової таблиці та натиснути ОК. Після цього буде створена порожня таблиця.

5.Збережіть створений файл у свою робочу папку під назвою labl.sta. При цьому достатньо ввести лише ім’я labl, розширення буде встановлене програмою автоматично.

Назви стовпчиків та рядків можна змінювати. Щоб змінити назву стовпчика (стовпчики по замовчуванню мають назви VAR1, VAR2...), виконайте подвійне натискання на його назві. Відкриється вікно, де у полі Name можна ввести нове ім’я для стовпчика. Якщо потрібно змінити назву рядка (рядки по замовчуванню нумеруються), треба виконати подвійне натискання на номері рядка та ввести з клавіатури його назву. Закінчити введення нової назви потрібно натисканням клавіші Enter.

6. Заповніть створену таблицю довільними значеннями, приблизно в межах від 0 до 100.

7. Ознайомтеся з призначенням і порядком розрахунку описових статистик у пакеті STATISTICA.

Розрахунок описових статистик

8. Відкрийте модуль Basic Statistics and Tables, призначений для розрахунку описових статистик, виконавши команди:

Статистика > Основна статистика/Таблиці

Вікно, що відкриється після виконання цієї команди, містить наступні інструменти аналізу:

Descriptive statistics (Описові статистики).

Correlation matrices (Кореляційні матриці).

t-test, independent (t-критерій для незалежних вибірок).

Застосовується, коли необхідно з’ясувати чи існує відмінність між середніми двох незалежних вибірок, при умові рівності дисперсій у цих вибірках. Рівність дисперсій перевіряється за допомогою F- критерію Фішера (який включений у таблицю виводу результатів t- критерію у STATISTICA).

Рис.3. Вікно - перемикач модулів пакету STATISTICA

t-test, dependent (t-критерій для залежних вибірок).

Breakdown & one-way ANOVA (Групування і однофакторний дисперсійний аналіз). Застосовується для дослідження відмінності декількох груп даних.

Frequency tables (Таблиці частот).

Tables and banners (Таблиці і заголовки).

Probability calculator (Розрахунок ймовірностей).

9.Для розрахунку описових статистик виберіть у вікні Basic Statistics and Tables (яке можна відкрити за допомогою команд Статистика > Основна статистика/Таблиці) пункт Descriptive statistics (Описові статистики) та натисніть ОК. Відкриється діалогове вікно Descriptive Statistics.

У вікні Descriptive statistics:

Виберіть змінні, для яких треба обчислити описові статистики. Для цього:

натисніть кнопку Variables: (Змінні)
у вікні, що відкриється, виберіть одну або декілька змінних (якщо необхідно вибрати всі змінні, натиснути кнопку Select All (Вибрати все)).
натисніть ОК.

Рис.4. Вікно переліку описових статистик

Обчисліть основні описові статистики. Для цього:

► натисніть кнопку Summary: descriptive statistics, або кнопку Summary. Відкриється вікно з таблицею результатів розрахунку основних описових статистик.

Valid N - кількість значень змінної (об’єм вибірки);

Mean - вибіркове середнє;

Minimum - мінімальне значення змінної;

Maximum - максимальне значення змінної;

Std.Dev - стандартне відхилення.

с) Обчисліть додаткові описові статистики. Для цього:

Відкрийте знов вікно Descriptive statistics, яке у мінімалізованому вигляді знаходиться у нижній частині вікна програми. Щоб відкрити це вікно, достатньо натиснути на ньому лівою кнопкою миші.

Рис.5. Вікно з таблицею результатів розрахунку основних описових статистик

У вікні Descriptive statistics перейдіть на вкладнику Advanced.

►Встановіть прапорець Conf.limits for means та у полі Interval:

(Надійна ймовірність) встановіть значення надійності для інтервальних оцінок описових статистик рівним 95%

У вікні Statistics встановіть прапорці навпроти статистик Median (медіана),Variance (дисперсія), Standard err. of mean (стандартна похибка середнього).

Натисніть кнопку Summary. Відкриється таблиця результатів розрахунку додаткових описових статистик.

Ознайомтеся з порядком графічного подання результатів статистичного дослідження дослідних даних у пакеті STATISTICA.

Графічне зображення описових статистик

Для наочного зображення описових статистик в пакеті STATISTICA застосовують, зокрема, графіки типу „ящик з вусами". Побудова „ящика з вусами" виконується у такій послідовності:

Відкрийте діалогове вікно Descriptive Statistics.

Якщо потрібно ,натисніть кнопку Variables: і виберіть змінні, для яких буде будуватися „ящик з вусами", ОК.
Перейдіть на вкладенку Options змініть прапорець біля Mean/SD/1.96*SD та встановіть прапорець Mean/SE/SD.

d) Перейдіть на вкладенку Quіск та натисніть кнопку Box & whisker plot for all variables (Графік „ящик з вусами" для всіх вибраних змінних).

На вкладниці Options можна вибрати наступні типи „ящиків з вусами"
Median/Quart./Range - Медіана/Квартилі/Границі.

Mean/SE/SD - Середнє/Стандартна похибка середнього/Стандартне відхилення.

Mean/SD/1.96*SD - Середнє/Стандартне відхилення/1.96*Стандартне відхилення.

Mean/SE/1.96*SE - Середнє/Стандартна похибка середнього/1.96*.

Стандартна похибка середнього (1.96 - значення t-критерію Ст´юдента для рівня надійності 95%, додаток 4). Наприклад, "ящики з вусами" типу Mean/SE/SD мають наступний вигляд (рис. 6).

Var1 Var2 Var3 Var4 Var5

Рис.6. Графік „ящик з вусами" для всіх вибраних змінних

На цьому графіку точка визначає положення середнього, стінки „ящика" - величину стандартної похибки середнього, „вуса" - величину стандартного відхилення.

Занотуйте основні відомості про пакет STATISTICА у свій робочий зошит.
Закрийте програму STATISTICA.

12.У робочому зошиті зробіть висновки відповідно до мети даної роботи.

Питання для самоконтролю

1.Навести основні модулі системи STATISTICA.

2.Вказати послідовність створення електронної таблиці.

3.Надати порядок відбору змінних, для яких треба

обчислити описові статистики.

4.Привести основні описові статистики.

5.Як визначається на графіку „ящик з вусами": вибірковосереднє, величина стандартної похибки середнього, величина стандартного відхилення.

Лабораторна робота №2
Первинна статистична обробка дослідних даних
в системи STATISTICA

Мета роботи:

Навчитися одержувати таблиці розподілу, будувати графіки розподілу, розраховувати основні статистичні параметри для вибірки (дослідних даних).

Завдання

В системі STATISTICA створити електронну - таблицю, яка зображена нижче (вона містить 4 стовпчики та 20 рядків) і зберегти її у свою робочу папку. Файлу дати назву 1аb2. sta.:

Використовуючи щойно створену таблицю з даними, виконати наступні завдання:

одержати таблиці розподілу (для кожної змінної окремо);
побудувати полігон і гістограму розподілу (для кожної змінної окремо), і порівняти їх вигляд з кривою нормального розподілу;
розрахувати точкові оцінки основних статистичних параметрів для вибіркових рядів (для кожної змінної окремо).

№ п.п	VAR1	VAR2	VAR3	VAR4
1	21,2	15,6	370	189
2	37,7	15,1	390	168
3	1,3	8,1	460	187
4	8,1	16,5	385	199
5	21,5	7,2	465	194
6	1,9	11,4	510	185
7	13,3	2,6	345	193
8	11,2	17,0	432	177
9	1,0	4,5	543	176
10	43,9	1,8	465	189
11	3,5	4,9	292	190
12	33,3	7,9	457	194
13	22,9	1,2	452	187
14	28,6	8,5	419	145
15	8	4	578	168
16	13.7	11,9	483	185
17	47	4,1	535	189
18	5,3	19,2	465	143
19	3,5	12,5	256	156
20	39,5	19,4	389	145

До числа описових статистик належать:

• кількість членів ряду - Valid (об’єм вибірки n);

• середнє арифметичне - mean (M = ∑V / n);

• стандартна похибка середнього арифметичного – Standart

err. of mean (m = σ / √ n);

• стандартне відхилення - сигма (Std.Dev.: σ = √ С / n – 1, або

σ = √ ∑ V²/ n);

• вибіркова дисперсія – Variance : (С = ∑ V² - (∑V)² / n);

• мода (Мо) - це значення ознаки або клас розподілу якій найбільш частіше зустрічається у вибіркової сукупності;

• медіана – Median (Ме) - це середнє значення ознаки яке

розділяє вибіркову сукупність на дві рівні частини;

• вибірковий коефіцієнт асиметрії - Skewness;

• вибірковий коефіцієнт ексцеса - Kurtosis;

• найбільше і найменше значення ряду – Min. & Max.;

• надійність (95%) - Conf. limits for means.

Хід роботи

Початок роботи і вибір змінних для аналізу

1.У вікні Статистика > Основна статистика/Таблиці вибрати пункт Descriptive statistics (Основна статистика) виберіть всі змінні для аналізу та натисніть ОК.

Побудова таблиць розподілу

2.Для одержання таблиць розподілу у вікні Descriptive statistics натисніть кнопку Frequency Tables (Таблиці розподілу).

Відкриються два вікна, де будуть подані таблиці розподілу для змінних VAR1 і VAR2 у наступному вигляді (рис.7).

Занотуйте у робочий зошит послідовність побудови полігону розподілу.

Лабораторна робота №3
Побудова діаграм і графіків у системі STATISTICA

Мета роботи:

Навчитися створювати і редагувати кругові і стовпчасті діаграми, графіки у системі STATISTICA.

Завдання

Створити нову електронну таблицю з даними і побудувати на основі цих даних кругову і стовпчасту діаграми.

Для виконання роботи використайте наступні дані про структуру поголів’я худоби у господарстві:

ВРХ - 816 гол., що складає 68%;

Свиней - 288 гол., 24%;

Овець - 60 гол., 5%;

Коней - 36 гол., 3%.

Хід роботи

Початок роботи

1.Запустіть програму STATISTICA.

Створіть новий файл електронної таблиці для введення даних, і збережіть цей файл під назвою Iab3.sta у свою робочу папку.

Параметри таблиці:

Число змінних «Number of variables» – 2.

Число регістрів «Number of cases» – 4.

2.Задайте у першому стовпчику iм´я змінної Вид тварин (VAR1), а у другому – Кількість тварин (VAR2) ( у режимі роботи з Специфікацією змінної).

Побудова кругової діаграми

2.Послідовно виконайте наступні команди у рядку меню:

Графіки > 2D графіки > Змішанні графіки.

Відкриється діалогове вікно Pie Charts (Кругові діаграми) (рис 12).

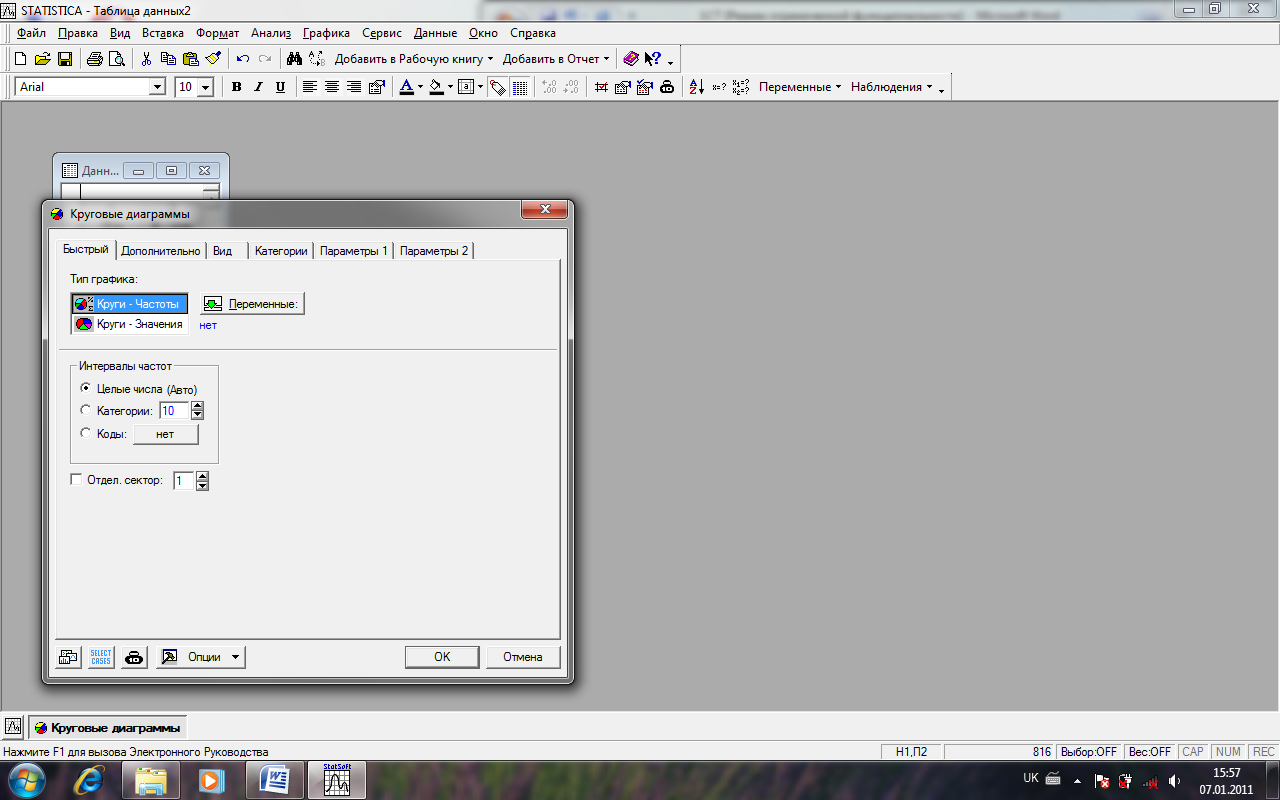
Рис.12. Вікно кругові діаграми Pie Chart

3.У вікні Pie Chart:

перейдіть на вкладинку Додатково (рис. 13);
через кнопку Змінні: введіть ім’я змінної VAR2, для якої задані числові дані;
у полі Тип графика виділіть рядок Pie Chart - Values (Діаграма для кількісних даних);
у полі Легенда шрифта: виділіть рядок Text and Percent (Назва і проценти), і у випадаючому списку Ярлики шрифта встановіть значення Case Names (Імена випадків). В цьому випадку біля відповідних секторів кругової діаграми будуть підписані назви худоби, які були введені, як назви випадків у перший стовпчик таблиці, і процент, який займає кожна худоба від загального поголів`я худоби.

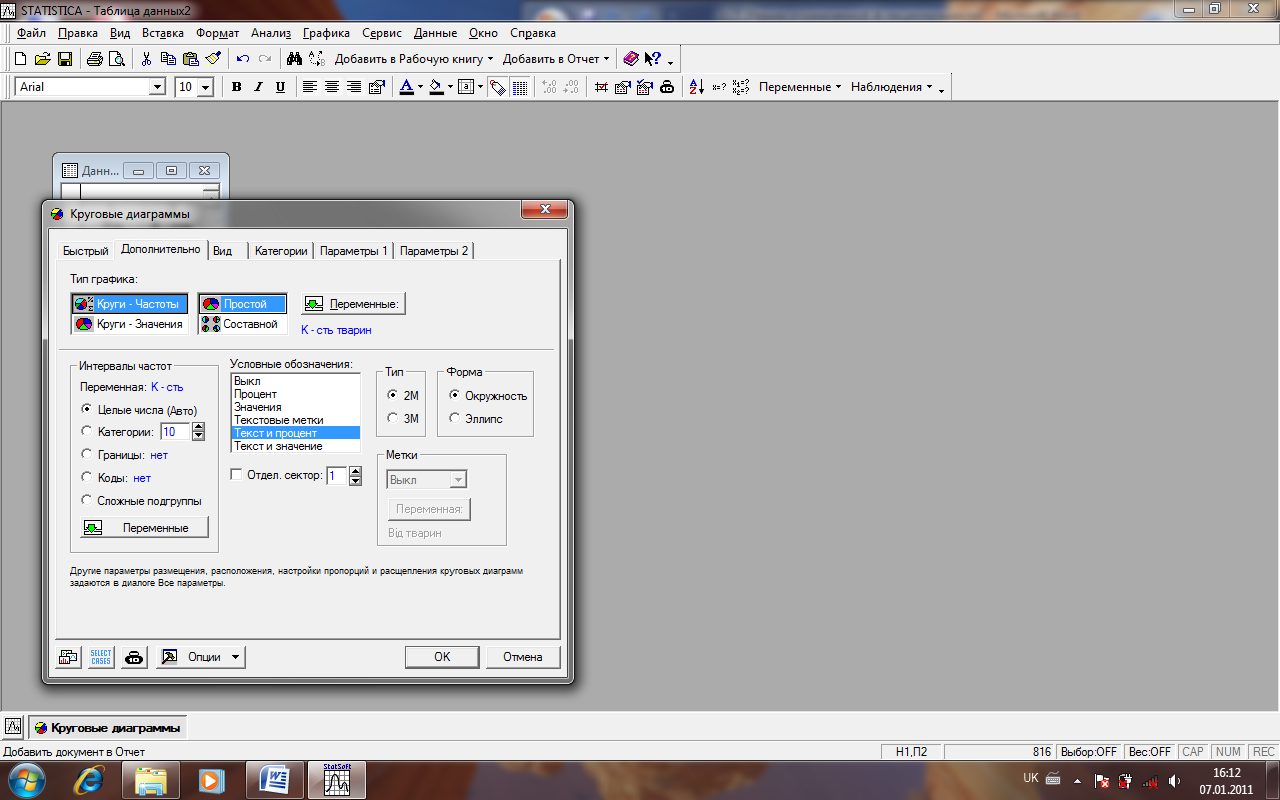
Рис.13. Вкладка Додатково вікна кругові діаграми

Якщо ж у полі Легенда шрифта: виділіти рядок Values (Значення), то біля відповідних секторів кругової діаграми стоятимуть вихідні дані (голови). Якщо виділити рядок Percent (Проценти), то на діаграмі буде позначено лише проценти). ОК.
Відкриється вікно, де буде побудовано кругову діаграму із заданими параметрами (рис. 14).

4.Збережіть побудовану діаграму у свою робочу папку у файлі з назвою Diag1 (командою File>Save as.).

5.Занотуйте у робочий зошит процедуру створення кругової діаграми.

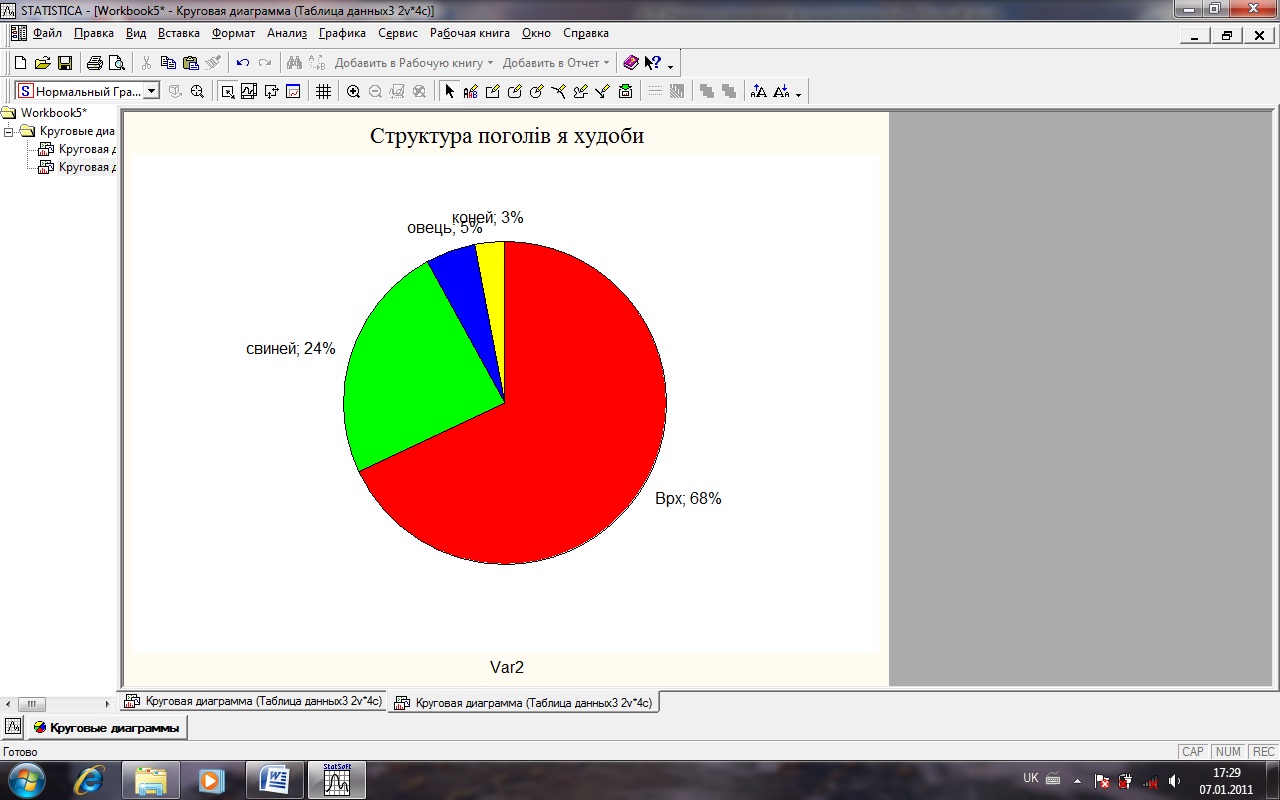
Рис. 14 Кругова діаграма із заданими параметрами

Редагування діаграми

Видалення непотрібних підписів

На цій діаграмі непотрібні верхній і нижній підписи. Тому, для покращення вигляду діаграми їх необхідно видалити.

5.Видаліть непотрібні підписи на діаграмі. Для цього натисніть лівою кнопкою на верхньому підписі та натисніть клавішуDelete на клавіатурі.

Так само видаліть нижній підпис.

Розміщення діаграми по центру вікна

Якщо діаграма розміщена не по центру вікна, або має занадто малі розміри, її параметри можна змінити.

6.Виконайте подвійне натискання лівою кнопкою мишки на білому фоні в області діаграми.

Відкриється діалогове вікно All Options на вкладинці Graph Window (рис. 15).

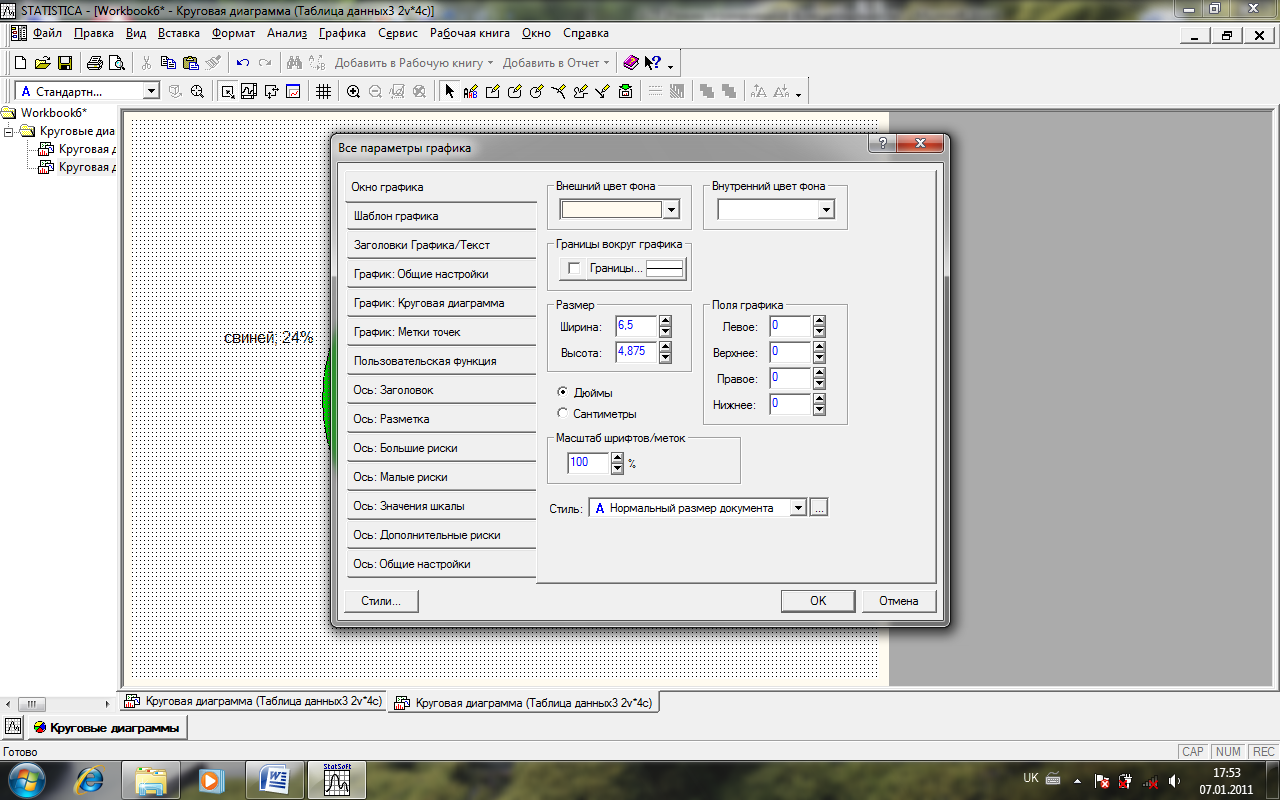
Рис.15. Вікно All Options (Усі параметри графіку)

У вікні All Options у розділі Graph margins встановіть вручну межі області графіку:

Left (Ліва) = 0,8

Тор (Верхня) = 0,5

Right (Права) = 0,8

Bottom (Нижня) = 0,2

ОК

Створення і редагування надпису на діаграмі

8.Створіть підпис „Рисунок 1" і розмістіть його знизу під діаграмою.

Для цього:

•Натисніть кнопку Text - на панелі інструментів. Курсор мишки набуде вигляду чорного хрестика.

Натисніть лівою кнопкою мишки у тому місці діаграми, де ви плануєте розмістити надпис. Утвориться текстове поле з надписом Custom text, який можна редагувати (змінювати).
Виконайте подвійне натискання лівою кнопкою мишки на створеному надписі. Відкриється вікно Graph Titles/Text, у робочому полі якого можна ввести свій текст.
Введіть текст: Рисунок 1 та натисніть ОК. Надпис буде створено.

Також у вікні Graph Titles/Text можна змінювати такі параметри тексту, як тип та розмір шрифту, його колір та деякі інші параметри.

9.Збережіть відредаговану діаграму свою робочу папку командою File > Save.

10.Занотуйте у робочий зошит основні моменти процедури редагування діаграми.

11.Закрийте вікно з круговою діаграмою.

Побудова стовпчастої діаграми

1.Виконайте команду:

Графіки > 2D графіки > Графіки Строки/Стовпчика

2.У вікні 2D Bar/Column Plots через кнопку Переменные: введіть ім’я змінної VAR2, для якої задані числові дані у полі Тип графіка виділіть рядок Regular (рис. 16). ОК.

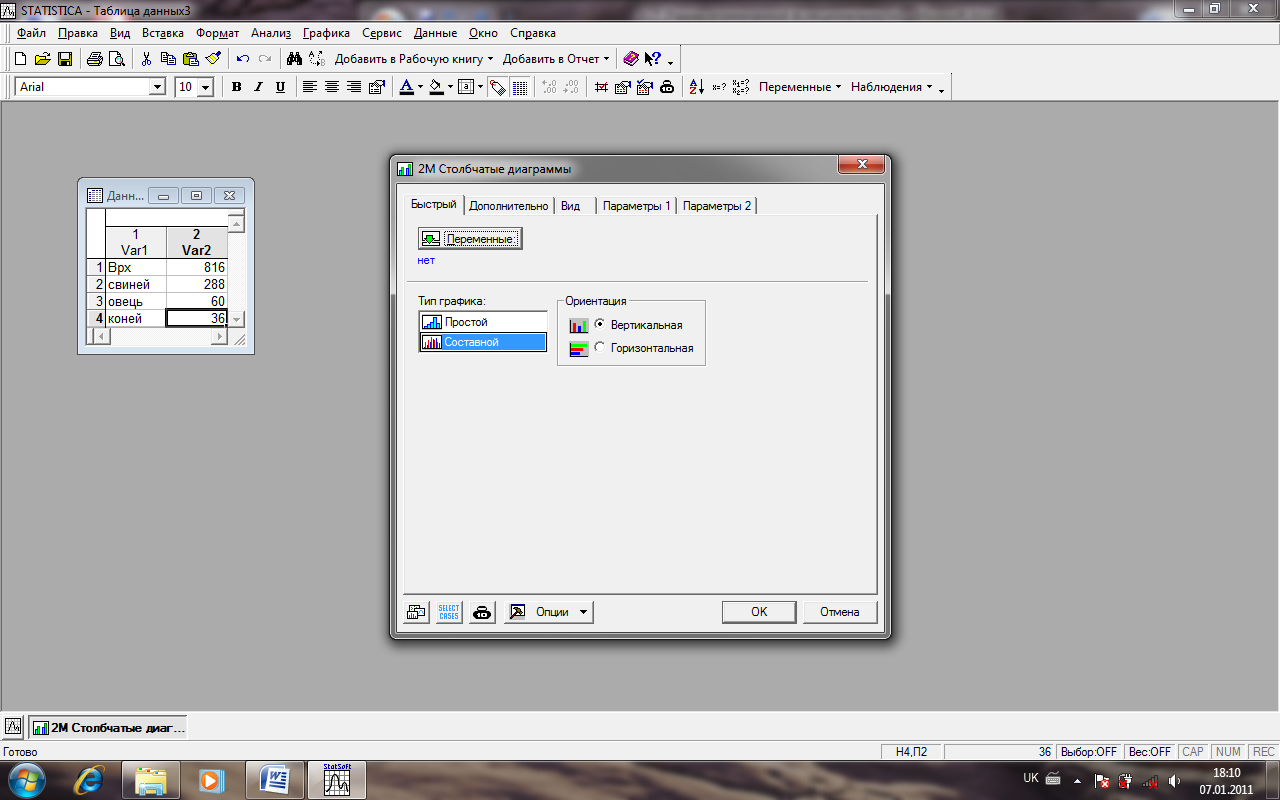
Рис. 16. Вікно параметрів будови стовпчастої діаграми

Відкриється вікно, де буде побудовано стовпчасту діаграму (рис. 17).

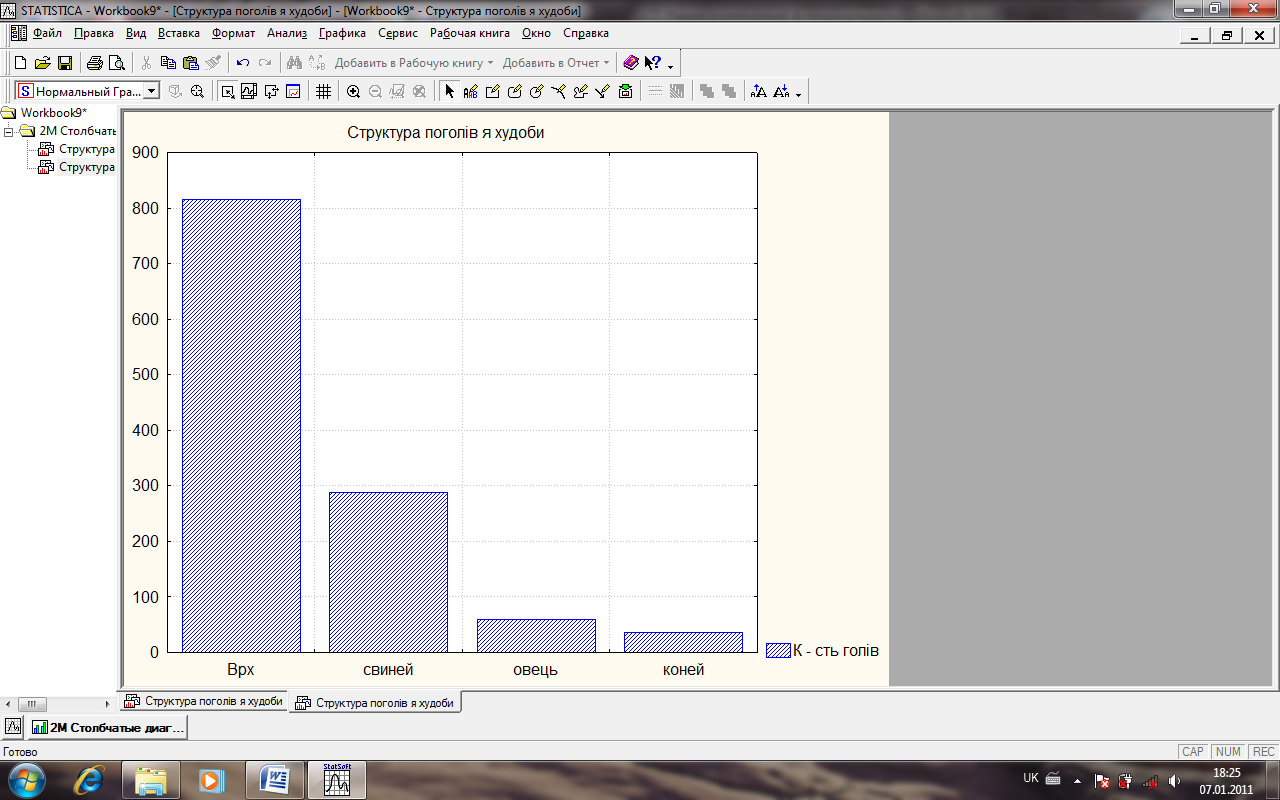
Рис. 17. Загальний вид стовпчастої діаграми

3.Збережіть побудовану діаграму у свою робочу папку у файлі з назвою Diag2.stw (командою File > Save as.).

Занотуйте у робочий зошит процедуру створення стовпчастої діаграми.

Видаліть зайві надписи на діаграмі.
Створіть в області діаграми нижнє поле шириною 0,2.
Створіть підпис "Рисунок 2" і розмістіть його знизу під діаграмою.
Збережіть відредаговану діаграму.

Зробіть висновки відповідно до мети даної роботи і занотуйте їх у робочий зошит.

Побудова графіків у системі STATISTICA

Завдання

а) Створити нову електронну таблицю з даними і побудувати на основі цих даних лінійний графік. Для виконання роботи використайте наступні дані про динаміку молочної продуктивності корів за 10 років (табл.1).

1.Динаміка молочної продуктивності корів, по роках

Роки	Надій корів за 305днів, кг
2001	4200
2002	3600
2003	3800
2004	3100
2005	3900
2006	3600
2007	3800
2008	4000
2009	4200
2010	4500

в) Створити нову електронну таблицю з даними і побудувати на основі цих даних трьохвимірний графік. Для виконання роботи використайте наступні дані про надій корів за 305днів в залежності від надію корів за 1 (VAR1) та 10 (VAR 10) міс. лактації, кг (табл. 2):

Хід роботи

Початок роботи

1.У своїй робочій папці створіть нову папку Іаb3. Всі файли, які буде створено при виконанні даної роботи, зберігайте у цій папці.

Запустіть програму STATISTICA.

2.Середньодобові надої корів по місяцях лактації, кг
Можли- вий надій за 305 днів лактації	Місяці лактації
Можли- вий надій за 305 днів лактації	І	II	111	IV	V	VI	VII	VIII	IX	X
2000	9,3	9,3	8,6	7,9	7,2	6,6	5,9	5,1	4,1	2,7
2100	9,9	9,9	9,7	8,3	7,6	6,9	6,2	5,3	4,3	2,9
2200	10,1	10,1	9,4	8,6	7,7	7,3	6,5	5,5	4,6	4,2
2300	10,5	10,5	9,8	9,0	7,8	7,5	6,8	5,9	4,3	3,4
2400	11,0	11,0	10,2	9,4	8,6	7,6	7,6	6,2	5,1	3,6
2500	11,4	11,4	10,6	9,7	9,0	8,2	7,4	6,5	5,3	3,9
2600	11,8	11,8	11,0	10,1	9,3	8,5	7,7	6,7	5,6	4,1
2700	12,2	12,2	11,4	10,5	9,6	8,9	8,0	7,0	5,9	4,3
2800	12,7	12,7	11,8	10,8	10,0	9,2	8,3	7,3	6,1	4,6
2900	13,1	13,1	12,2	11,2	10,3	9,5	8,6	7,6	6,4	4,8
3000	13,5	13,5	12,5	11,6	10,9	9,8	8,9	7,8	6,6	5,1
3100	13,9	13,9	12,9	11,9	11,0	10,1	9,2	8,1	6,9	5,3
3200	14,4	14,4	13,3	12,3	11,3	10,4	9,5	8,4	7,1	5,5
3300	14,8	14,8	13,7	12,7	11,7	10,6	9,8	8,7	7,4	5,8

Завдання А

Створіть новий файл електронної таблиці для введення даних з табл. 3.1. і збережіть цей файл під назвою Iab3_1.sta у свою робочу папку Іаb3.
Задайте у першому стовпчику ім’я змінної Роки, а у другому - Надій корів.

Таблиця повинна мати наступний вигляд (рис. 18).

Послідовно виконайте наступні команди:
Графіки > 2D графіки > Графіки лінії (Змінні).

Відкриється діалогове вікно 2D Line Plots (2-вимірні лінійні графіки) (рис. 20).

У вікні 2D Line Plots:

перейдіть на вкладинку Додатково;
у полі Тип графіка: виділіть рядок XY Trace (XY-

лінія);

Рис. 18. Побудова лінійного графіку

Рис. 19. Діалогове вікно 2D Line Plots

Потім кнопкою Змінні: відкрийте вікно Select Variables for Trace Plot (Вибір змінних для лінійного графіку), і виберіть у лівій частині вікна незалежну (факторну) змінну Роки (X), а у правій частині залежну (результативну) змінну Надій корів (Y); ОК;

• у полі підгонка залиште значення Off (Вимкнено); ОК.

Відкриється вікно, де буде побудовано лінійну діаграму із заданими параметрами (рис. 20).

Рис. 20. Лінійна діаграма із заданими параметрами

Збережіть побудований графік у свою робочу папку у файл з ім’ям LinGraph (командою File > Save as...).
Занотуйте у робочий зошит процедуру створення лінійного графіку.

Редагування лінійного графіку

Видаліть верхній підпис на графіку за допомогою клавіші Delete.
Задайте в області графіка нижнє поле шириною 1.

10.Створіть у нижньому полі підпис „Рисунок 1. Лінійний графік".

11.Методом перетягування розмістіть підпис у нижньому полі області графіку (рис.21).

12.Збережіть відредагований графік у свою робочу папку Іаb4 командою File > Save.

Закрийте вікно з лінійним графіком.

13.Створіть нову електронну таблицю для введення даних з табл.2. Введіть дані з табл. 2. і збережіть її у свою робочу папку Іаb3 у файл з назвою Iab3_2.sta.

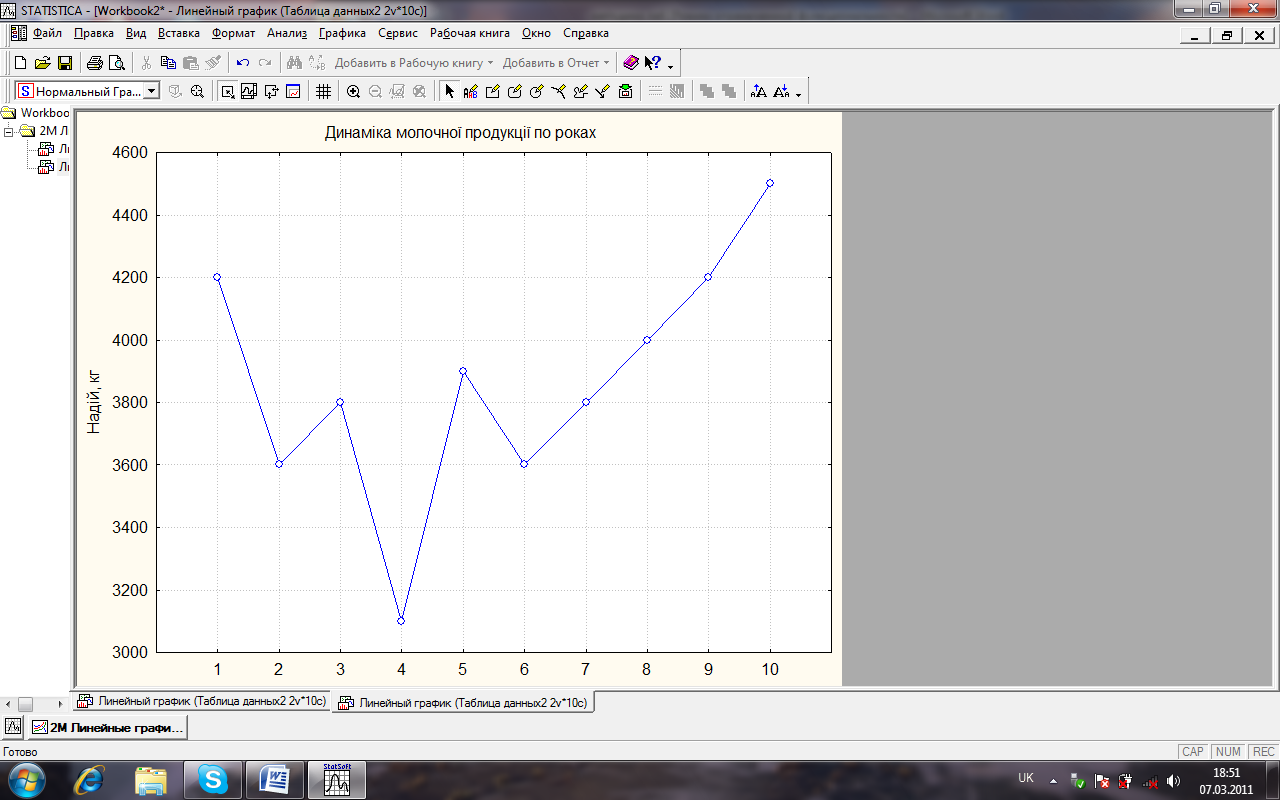
Рис. 21. Відредагований лінійний графік

Завдання В

Таблиця повинна мати наступний вигляд (рис. 22):

Рис. 22 .Вікно - Електрона таблиця

Побудова трьохвимірного графіку

14.Після створення таблиці виконайте команди:

Графіки > 3D XYZ графіки > Поверхність графіків.

Відкриється діалогове вікно 3D Surface Plots (3-вимірні поверхні) (рис. 23).

Рис. 23. Діалогове вікно 3D Surface Plots (3-вимірні поверхні)

15.У вікні 3D Surface Plot спочатку через кнопку Змінні виберіть змінні таким чином:

у першому стовпчику X – надій за 1 міс.,

у другому стовпчику Y – надій за10 міс.,

у третьому стовпчику Z - надій за лактацію;

у полі Подгонка встановіть значення Distance Weighted LS (Метод найменших квадратів); ОК.

Відкриється вікно, де буде побудовано 3-х вимірний графік (рис. 24).

16.Збережіть побудований графік у свою робочу Іаb3 папку у файл з ім’ям Surface (командою File > Save as.).

Рис. 24. Трьохвимірний графік

Занотуйте у робочий зошит процедуру створення 3-вимірного графіку.

Редагування 3-вимірного графіку

17.Видаліть верхні підписи на графіку.

18.Задайте в області графіка нижнє поле шириною 0,8.

19.Створіть у нижньому полі підпис „Рисунок 2. Графік поверхні".

Методом перетягування розмістіть підпис у нижньому полі області графіку.

20.Збережіть відредагований графік у свою робочу папку Іаb3 (File > Save ).

Уважно роздивіться графік. Зробіть висновок, як залежить молочна продуктивність корів від надою корів за 1-й та 10 міс. лактації.

Рис. 26. Графік поверхні

Занотуйте цей висновок у свій робочий зошит. Зробіть висновки відповідно до мети даної роботи і занотуйте їх у робочий зошит.

Питання для самоконтролю

1.Мета та завдання будови діаграм.

2.Вказати різновиди діаграм.

3.Призначення діалогового вікна Pie Charts пакету

STATISTICA.

4.Вказати різницю між випадаючими вікнамі:

2D Line Plots та 3D Surface Plots.

Лабораторна робота №4

Порівняння статистичних рядів у системі STATISTICA

Мета роботи:

Навчитися процедурам використання критеріїв Ст’юдента (t-тест) і Фішера - Снедекора (F-тест) для порівняння між собою двох вибірок (незалежних та залежних) у системі STATISTICA.

Завдання

1.Порівняти дві незалежні вибірки

Досліджувалася жирномолочність та надій за лактацію корів Української чорно рябої молочної - УЧРМ (контрольна) та Голштинської (дослідна) порід в однакових умовах утримання.

Одержані дані були занесені в таблицю (табл. 4.1).

Потрібно визначити, чи є достовірною статистична відмінність між жирномолочністю корів різних порід; чи можна статистично достовірно стверджувати, що жирномолочність корів обох порід варіює однаково.

Хід роботи

Початок роботи

1.У своїй робочій папці створіть нову папку Іаb4. Всі файли, які будуть створенні при виконанні даної роботи, зберігайте у цій папці.

Запустіть програму STATISTICA.

Завдання А

2.Створіть новий файл електронної таблиці для введення даних з табл. 3.

Збережіть цей файл під назвою Iab4_1.sta у свою робочу папку Іаb4.

3.Надайте змінним імена відповідно Дослід і Контроль.

4.1.Жирномолочність та надій молока за лактацію від корів.

Розрахунок описових статистик і формулювання статистичних гіпотез

4.Перейдіть до підмодуля Descriptive Statistics (Описові статистика) і розрахуйте: кількість значень змінної (об’єми вибірок Valid) n₁, n₂; середні значення (Mean) Х_l і Х₂; стандартні похибки середніх арифметичних (Standart err. of mean m₁і m₂): та дисперсії (Variance) V_l і V₂ для обох змінних.

3.Продуктивність корів дослідних груп

№ пп	Вміст жиру у молоці корів, (%)		Надій за лактацію (кг)
№ пп	Дослідна (Голштинська)	Контрольна (УЧРМ)	Дослідна (Голштинська)	Контрольна (УЧРМ)
1	3,6	3,7	6350	6016
2	3,5	3,6	6570	5875
3	3,8	3,7	6560	6238
4	3,5	3,4	6830	6124
5	3,4	3,7	6185	5782
6	3,6	3,4	6438	5868
7	3,7	3,6	6037	5945
8	3,8	3,7	5946	5478
9	3,7	3,5	6457	6012
10	3,6	3,5	6348	6548
11	3,5	3,7	6157	5276
12	3,3	3,7	6045	5476
13	3,4	3,5	6378	5846
14	3,6	3,3	6846	5465
15	3,7	3,4	6842	5985
16	3,6	3,7	5912	5826
17	3,7	3,6	6743	5745
18	3,4	3,4	6879	6275
19	3,4	3,5	6754	5786
20	3,5	3,6	6589	5674

Занотуйте розраховані значення середніх у свій робочий зошит і порівняйте їх між собою.

5.Сформулюйте нульову гіпотезу щодо середніх Н₁₀ у наступній формі:

"Нульова гіпотеза Н₁₀ полягає в тому, що істотної (значущої) відмінності між середньою живою масою корів двох порід немає, і відмінність між середніми, що спостерігається у досліді, можна пояснити випадковими причинами. Тобто Н¹₀: х₁ = х₂".

Занотуйте її у свій робочий зошит.

6.Сформулюйте нульову гіпотезу щодо дисперсій Н₂₀ у наступній формі:

"Нульова гіпотеза Н₂₀ полягає в тому, що істотної (значущої) відмінності між дисперсіями значень живої маси двох порід немає, і відмінність між дисперсіями, що спостерігається у досліді, можна пояснити випадковими причинами. Тобто Н²₀ : V₁ = V₂".

Занотуйте її у свій робочий зошит.

Закрийте вікно з результатами розрахунків.

Перевірка гіпотези про нормальний розподіл

Параметричні статистичні критерії, до яких відносяться t-тест Ст’юдента і F-тест Фішера - Снедекора, застосовують для попарного порівняння нормально розподілених статистичних рядів. Тому, до порівняння рядів за допомогою цих критеріїв, необхідно переконатися, що розподіл даних рядів близький до нормального. Для цього у системі Statistica можна використати "нормальний ймовірностний аркуш".

6.У вікні Descriptive Statistics (Описові статистики) (рис. 27) виділіть змінні (Все) та натисніть кнопки Нормальність та Гістограми. Відкриються вікна, де на так званих ‘"нормальних ймовірнісних аркушах" буде побудовано графік, що відповідає нормальному розподілу (червона лінія) та гістограма, що відповідає розподілу статистичного ряду, що досліджується (рис. 28). Якщо гістограма не дуже відрізняється від червоної лінії, то можна стверджувати, що даний статистичний ряд має розподіл, близький до нормального.

Рис.27. Вікно Descriptive Statistics (Описові статистики)

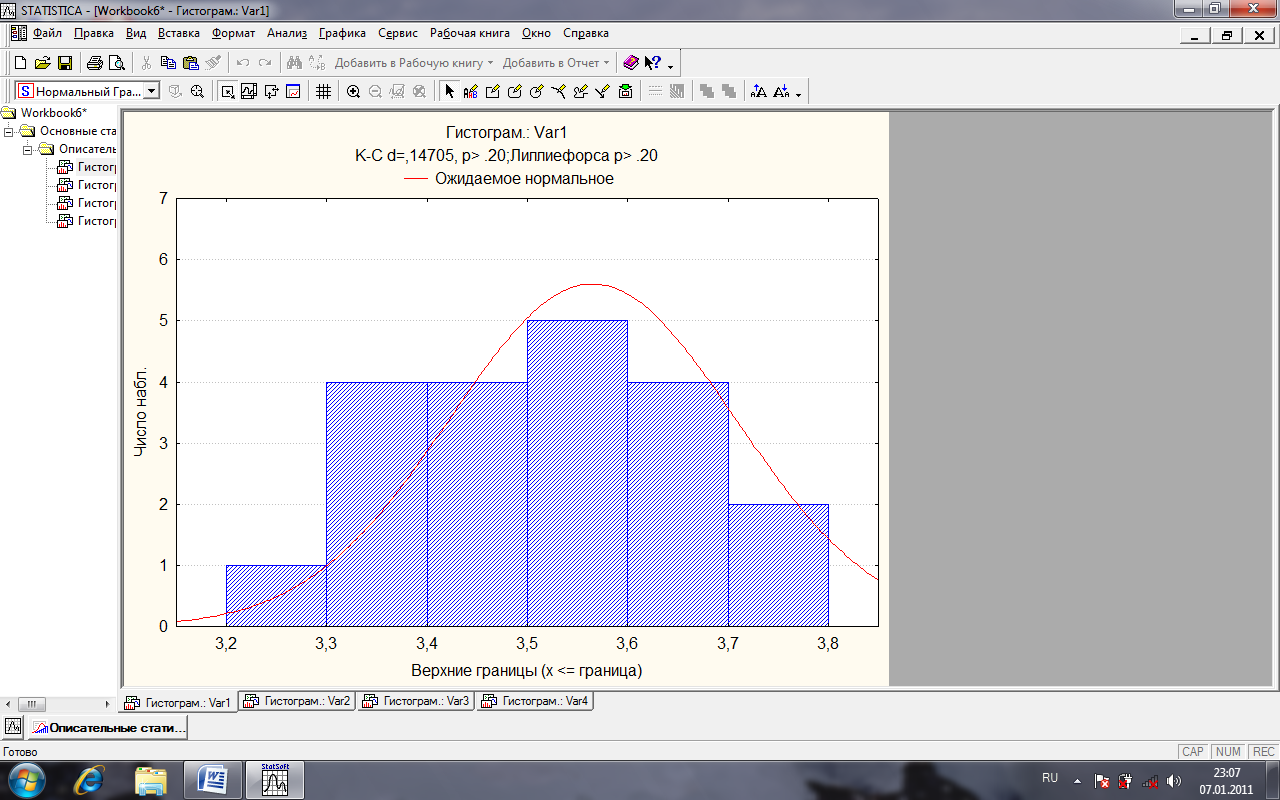
Рис. 28. Вікно нормального імовірнісного розподілу

7.Роздивіться графіки розподілів змінних Дослід і Контроль на нормальному імовірнісному розподілу і сформулюйте висновок про те, наскільки розподіли цих змінних близькі до нормального розподілу і про можливість застосування параметричних статистичних критеріїв до порівняння двох даних статистичних рядів, у наступному вигляді:

"Точковий графік змінної Дослід/Контроль на нормальному імовірнісному розподілі майже не відрізняється/відрізняється від графіку нормального розподілу. Тому можна стверджувати, що змінна Дослід/Контроль має розподіл, близький/далекий від нормального, і для порівняння даних статистичних рядів можна/не можна.

8.Закрийте вікна з графіками і вікно Descriptive Statistics.

Занотуйте у робочий зошит процедуру перевірки гіпотези про нормальний розподіл за допомогою нормального ймовірностного аркушу.

Перевірка гіпотези про рівність середніх (t-тест)

У припущенні, що дані статистичні ряди мають розподіл, близький до нормального, для перевірки гіпотези Н₁₀ про рівність середніх використовується t-критерій Ст’юдента (t-тест).

9.У вікні модуля Basic Statistics/Tables виберіть рядок t-test, independent, by variables (t-тест для незалежних вибірок (змінних)). ОК.

Зауваження. Дослідження проводились на коровах різних порід, тому можна вважати вибірки незалежними.

10.У вікні T-Test for Independent Samples by Groups встановіть такі значення параметрів: натисніть кнопку Variables (groups): (Змінні (групи) і у вікні Select two variable lists (lists of groups) (Виберіть два списка змінних (списки груп) виберіть змінні для порівняння: у першому стовпчику - змінну Дослід, а у другому - змінну Контроль. ОК.

Перевірте, щоб у вікні T-Test for Independent Samples (Groups) було зазначено First list: (Перший список:) Дослід, Second list: (Другий список:) Контроль. ОК.

Для проведення t-тесту натисніть кнопку Summary: T-tests ( t-критерий для незалежних вибірок ) (рис.29).

Рис. 29. Вікно основини статистики і таблиці

У вікні T-test for independent samples (Iab4_1.sta) з’являться результати розрахунків (рис. 30).

Розрахуйте оцінки різності вибіркових середніх.

Перший критерій різності вибіркових середніх (Ст’юдента) ( t_d ≥ t_st при умові кількості ступенів вільності γ = n₁ + n₂ - 2):

t_d = (M₁ – M₂) / √ m²₁ + m²₂,

Mean Group 1 (середнє першої вибірки) = (M₁=3,70)_________;

Mean Group 2 (середнє другої вибірки) = (М₂=3,60)_____________;

t_d -value (спостережене) = ________;

γ - (кількість ступенів вільності) = _________;

Р - рівень значущості за Ст’юдентом (t_st), (додаток 4) = _

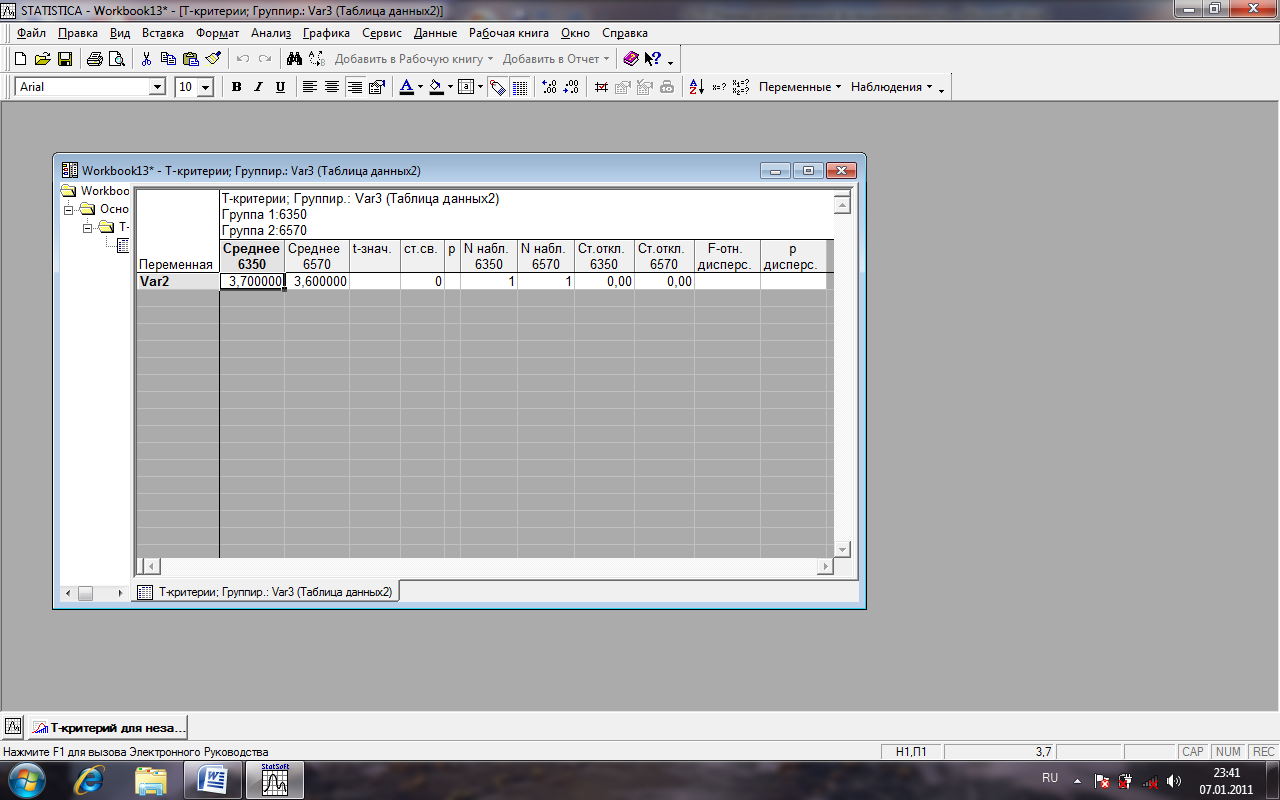
Рис. 30. Вікно Т - критерія

Другій критерій різності вибіркових середніх (Фішера) (F_d ≥ F_st при умові кількості ступенів вільності: γ₁ = 1; γ₂ = n₁ + n₂ - 2):

F_d = ((M₁ – M₂)² / σ²_z) × (n₁ × n₂) / n₁ + n₂.

σ²_z = (n₁ - 1) σ²₁+ (n₂ - 1) σ²₂ / (n₁ + n₂ - 2)

Р - (рівень значущості за Фішером (t_st), додаток 5) = ____

Випишіть результати розрахунків у свій робочий зошит:

Зауваження. Рівень значущості (Р) головне, що необхідно знати, щоб прийняти рішення про справедливість, або хибність нульової гіпотези Н₀. Рівень значущості вказує ймовірність справедливості нульової гіпотези. Звичайно, в біологічних дослідженнях, якщо рівень значущості Р<0,05, то нульова гіпотеза Н₀ вважається хибною (відкидається). При рівні значущості Р>0,05, нульова гіпотеза Н₀ вважається справедливою (приймається).

11. Виходячи з розрахованого значення рівня значущості (Р), сформулюйте аргументований висновок щодо нульової гіпотези Н₁₀ у наступній формі:

"Розрахований рівень значущості Р =.________ .Це менше/більше, ніж заданий рівень довіри 0,05. Тому нульова гіпотеза Н₀, яка полягає в тому, що істотної (значущої) відмінності між жирномолочністю корів різних порід немає, хибна/справедлива.

Занотуйте цей висновок у свій робочий зошит.

12. На основі попереднього висновку сформулюйте відповідь на першу частину завдання А у наступній формі:

Оскільки нульова гіпотеза Н¹₀, яка полягає в тому, що істотної (значущої) відмінності між жирномолочністю корів різних порід немає за результатом t-тecmy виявилася хибною/справедливою, то можна стверджувати, що середня жирномолочність корів різних порід статистично достовірно відрізняється/не відрізняється при заданому рівні довіри 0,05.

Занотуйте у робочий зошит процедуру перевірки гіпотези про рівність середніх двох статистичних рядів (t-тест).

Перевірка гіпотези про рівність дисперсій (F-тест)

У припущенні, що дані статистичні ряди мають розподіл, близький до нормального, для перевірки гіпотези Н₂₀ про рівність дисперсій використовується F-критерій Фішера-Снедекора (F-тест).

13. Для проведення F-тесту використовують також кнопку T-tests.

У вікні T-test for independent samples (Iab4_1.sta), крім результатів розрахунків, що були виписані вище (п. 11), є також інші результати.

Випишіть їх у свій робочий зошит: F-ratio Variances (значення F-критерію) = _____________.

P Variances (рівень значущості) для порівняння дисперсій = ________.

14. Виходячи з розрахованого значення рівня значущості Р variances, сформулюйте аргументований висновок щодо нульової гіпотези Н₂₀ у наступній формі:

«Розрахований рівень значущості Р variances =______.

Це менше/більше, ніж заданий рівень довіри 0,05. Тому нульова гіпотеза Н₂₀, яка полягає в тому, що істотної (значущої) відмінності між дисперсіями значень жирномолочності корів двох різних порід немає, хибна/справедлива.

Занотуйте цей висновок у свій робочий зошит.

14. На основі попереднього висновку сформулюйте відповідь на другу частину завдання А у наступній формі:

"Оскільки нульова гіпотеза Н²₀, яка полягає в тому, що істотної (значущої) відмінності між дисперсіями значень жирномолочності корів різних порід за результатом F-тесту виявилася хибною/справедливою, то можна стверджувати, що дисперсія значень жирномолочності корів у дослідної групі статистично достовірно відрізняється/не відрізняється від дисперсії значень жирномолочності корів контрольної групі при заданому рівні довіри 0,05.

Занотуйте цей висновок у свій робочий зошит.

Занотуйте у робочий зошит процедуру перевірки гіпотези про рівність дисперсій двох статистичних рядів (F-тест).

Наочне порівняння - "ящик з вусами"

15. Для наочності порівняння побудуйте графік типу "ящик з вусами" для обох змінних. Для цього треба знов відкрити вікно Т- Test for Independent Samples by Variables і у ньому натиснути кнопку Box & whisker plot (рис 31).

Висновки по суті завдання А

Зробіть змістовний висновок про переваги тієї чи іншої породи з жирномолочності корів.

Занотуйте висновок у свій робочий зошит.

Закрийте всі відкриті вікна і закрийте програму STATISTICA.

Питання для самоконтролю

1. Мета перевірки гіпотези про нормальний розподіл аналізуючих ознак.

2. До яких статистичних критеріїв відносяться t-тест Ст’юдента і F-тест Фішера – Снедекора.

3. Якщо гістограма не дуже відрізняється від червоної лінії, то можна стверджувати, що…. ?

4. В біологічних дослідженнях, прі якому рівні значущості (Р) нульова гіпотеза Н₀ вважається хибною (відкидається).

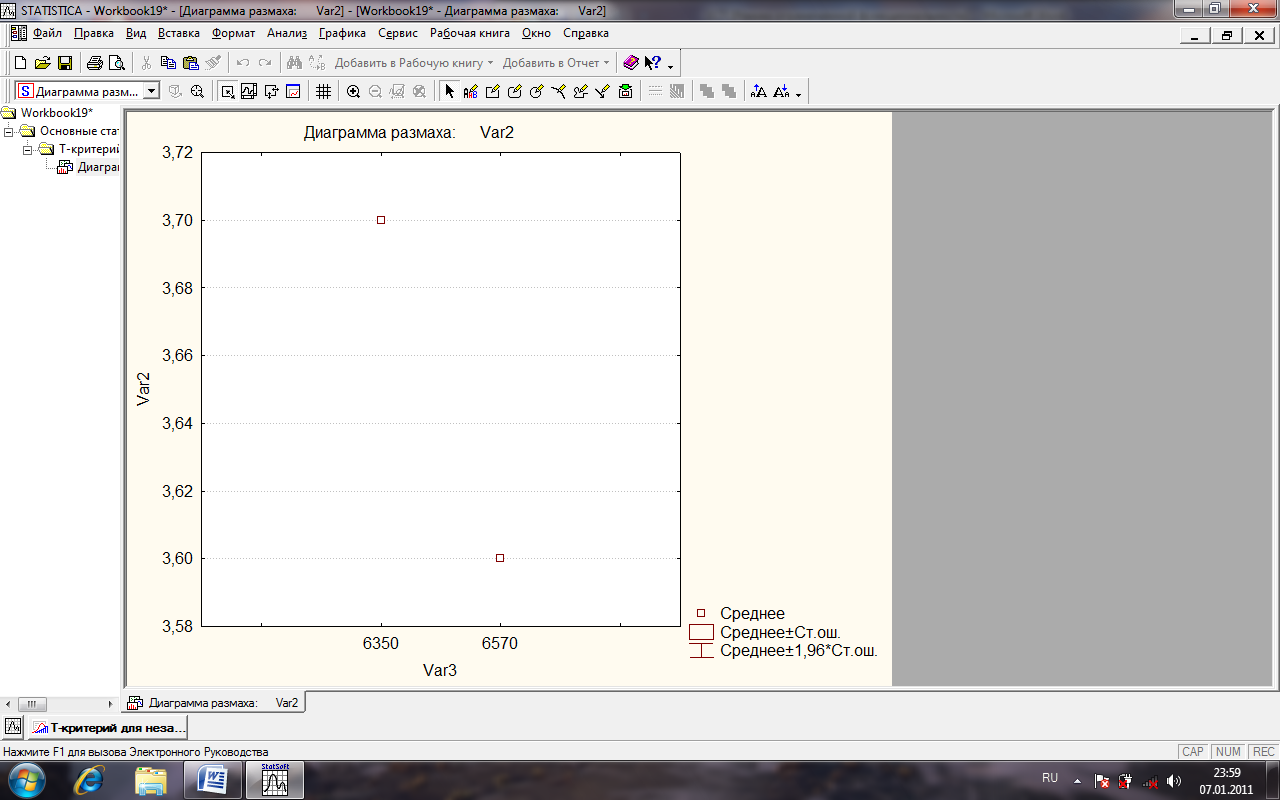
Рис. 31. Графік типу "ящик з вусами" для обох змінних Box & whisker plot

Лабораторна робота 5

Проведення кореляційного аналізу у системі STATISTICA

Мета роботи:

Навчитися процедурі проведення повного кореляційного аналізу у системі STATISTICA.

Зауваження. Мета кореляційного аналізу - виявити наявність і силу (тісноту) лінійного зв’язку між деякими двома змінними. Для цього необхідно розрахувати коефіцієнт парної кореляції, який є показником тісноти лінійного кореляційного зв’язку, і може приймати значення у межах від -1 до +1. У випадку, коли залежність між змінними є більш складною, ніж лінійний зв’язок, коефіцієнт кореляції прийме значення 0, що означає відсутність лінійного зв’язку, але не означає відсутності зв’язку взагалі. Оскільки ми маємо справу з випадковими величинами, то необхідно також перевірити значущість коефіцієнта кореляції, тобто перевірити чи істотно він відрізняється від нуля.

Завдання

Провести кореляційний аналіз зв’язку між середньодобовим надоєм і відсотком жиру у корів за 12 - річний період (табл. 4):

4. Динаміка надою та % жиру у корів по роках

Роки	Показники продуктивності
Роки	Середньодобовий надій, кг	% жиру
1991	11,5	3,7
1992	10,2	3,9
1993	8,8	4,2
1994	8,6	4,3
1995	9,6	4,0
1996	10,2	4,1
1997	7,9	3,9
1998	8,8	4,2
1999	9,6	4,1
2000	10,5	3,8
2001	11,1	3,5
2002	12,4	3,6

Початок роботи

1. У своїй робочій папці створіть нову папку Іаb5. Всі файли, які буде створено при виконанні даної роботи, зберігайте у цій папці.

2. Запустіть програму STATISTICA і створіть новий файл електронної таблиці для введення даних з табл. 5.1. (рис. 32).

Збережіть цей файл під назвою Iab5.sta у свою робочу папку Іаb5.

Побудова діаграми розсіяння

Процедура кореляційного аналізу розпочинається з візуального аналізу кореляції. Для цього будується діаграма розсіяння, яка дозволяє одержати загальне наочне уявлення про характер залежності між двома змінними.

3. Кнопкою STATISTICA на панелі інструментів викличте вікно Основна статистика і переключіться до модуля Correlation matrices (Кореляційні матриці), ОК .

Рис.32.Електронна таблиця для введення даних

Відкриється вікно Pearson Product-Moment Correlation (Кореляційні показники Пірсона) (рис.33).

Рис 33. Кореляційні показники Пірсона

4. У вікні Pearson Product-Moment Correlation клацніть кнопку One variable lists (square matrix) (Один список змінних (квадратна матриця)) і виберіть обидві змінні для аналізу кнопкою Select All, OK (рис.34).

Рис.34. Вікно відбору змінних

5. Далі перейдіть на вкладинку Advanced/plot та натисніть кнопку with casenames (3 іменами), що знаходиться біля кнопки 2D scatterplots (2-вимірні розсіяння).

6. Відкриється вікно Select two var. lists (horizontal and vertical vars in plots): (Вибір змінних для аналізу).

7. У вікні Select two var. lists (horizontal and vertical vars in plots):

виберіть у першому стовпці змінну Надій, а у другому - % жиру, і клацніть OK.

8. Буде побудовано 2-вимірну діаграму розсіяння (рис.35).

9. Збережіть діаграму розсіяння у свою робочу папку Іаb5 у файлі з назвою Diag_Roz.

10. Роздивіться уважно діаграму розсіяння і зробіть попередні висновки, щодо характеру залежності між змінними Надій і % жиру.

Занотуйте ці попередні висновки у робочий зошит.

Рис.35. 2-вимірна діаграму розсіяння

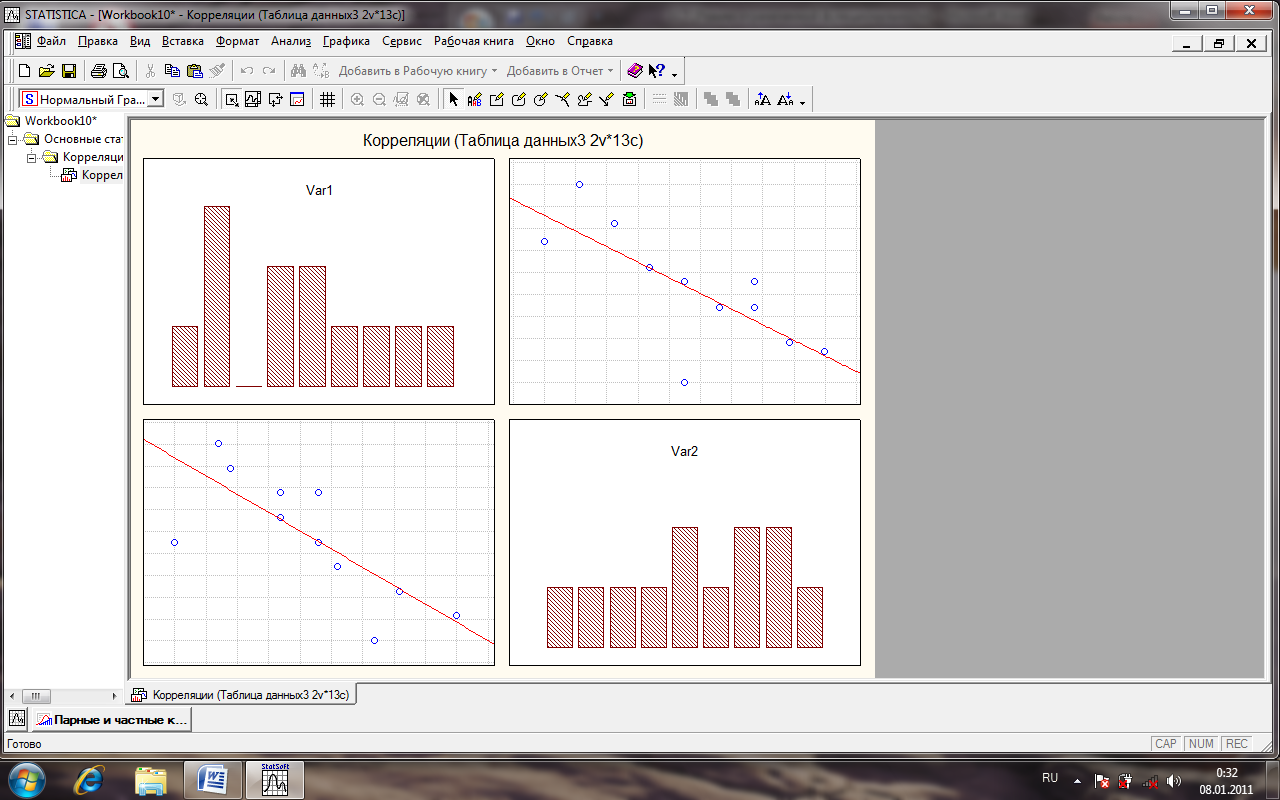
Рис.35. Вікно з виводу 2-вимірної діаграми розсіяння ознак

Розрахунок коефіцієнтів кореляції

11. У вікні щойно побудованої діаграми клацніть кнопку Continue... і поверніться у вікно Product-Moment and Partial Correlation (воно у мінімалізованому вигляді знаходиться у нижній частині вікна програми).

12. У вікні Product-Moment and Partial Correlation клацніть кнопку Summary:Correlations matrix (Кореляції). Відкриється вікно Correlations (Iab6.sta) з розрахованою матрицею коефіцієнтів кореляції (рис.36).

13. Збережіть кореляційну матрицю у свою робочу папку Іаb4 у файлі з назвою Kor Мatr.Str.

Рис.36. Вікно Product-Moment and Partial Correlation

Роздивіться матрицю коефіцієнтів кореляції у вікні Correlations (Iab5.sta) (рис.37).

Рис.37. Квадратна матриця коефіцієнтів кореляції

Занотуйте у робочий зошит процедуру одержання кореляційної матриці.

14. Занотуйте у робочий зошит значення коефіцієнту кореляції змінних Надій і % жиру.

15. Зробіть попередній висновок щодо сили лінійного кореляційного зв’язку між двома змінними надій і % жиру і занотуйте його у робочий зошит.

Для формулювання висновку використовуйте наступну умовну градацію значень коефіцієнту кореляції:

до 0,3 - слабкий лінійний зв’язок;

від 0,3 до 0,5 - помітний лінійний зв’язок;

від 0,5 до 0,7 - помірний лінійний зв’язок;

від 0,7 до 0,9 - тісний лінійний зв’язок;

понад 0,9 - дуже тісний лінійний зв’язок.

Перевірка значущості коефіцієнта кореляції

Коефіцієнт кореляції за своєю природою є випадковою величиною, як і всі інші точкові оцінки статистичних показників. Тому обов’язковим елементом кореляційного аналізу є перевірка значущості коефіцієнту кореляції.

Значущість означає, що коефіцієнт кореляції істотно відмінний від нуля. Якщо коефіцієнт кореляції виявиться значущим, то він відображає дійсно існуючу лінійну кореляційну залежність між двома величинами. Якщо ж він виявиться незначущим, то насправді лінійної кореляційної залежності між величинами немає. В цьому, останньому, випадку попередні висновки (див. вище) є помилковими, і кореляція, що спостерігається у досліді, пояснюється лише випадковими причинами, а не є відображенням дійсно існуючого зв’язку.

При розрахунку кореляційної матриці пакет STATISTICA одночасно виконує перевірку значущості коефіцієнту кореляції. Перевіряється нульова гіпотеза Н_о про те, що коефіцієнт кореляції дорівнює нулю (тобто є незначущим).

Якщо розраховані значення коефіцієнту кореляції у таблиці подано червоним кольором, то нульова гіпотеза Н_о відкидається. Тобто коефіцієнт кореляції є значущим (істотно відмінним від нуля) при заданому рівні значущості Р = 0,05 (див. верхній рядок таблиці), і характеризує дійсно існуючу лінійну кореляційну залежність між двома величинами. Тоді всі попередні висновки є справедливими.

Якщо ж значення подано чорним кольором, то коефіцієнт кореляції є незначущим (може дорівнювати нулю) при заданому рівні значущості Р=0,05.

Це означає, що насправді лінійного кореляційного зв’язку між величинами немає, і всі попередні висновки не мають під собою ніяких підстав.

Розгляньте таблицю коефіцієнтів кореляції у вікні Correlations (Iab6.sta) і сформулюйте висновок про значущість коефіцієнту кореляції, враховуючи сказане вище. Занотуйте цей висновок у робочий зошит.

Графічне подання результатів кореляційного аналізу

Якщо коефіцієнт кореляції виявився значущим, то це означає, що між змінними Надій і % жиру дійсно існує лінійний статистичний зв’язок певної сили. Тоді має сенс побудувати і проаналізувати графік, що відображає цю лінійну залежність.

Для продовження аналізу клацніть кнопку Continue.. у вікні Correlations (Iab6.sta) і поверніться у вікно Product-Moment and Partial Correlation.

У вікні Pearson Product-Moment Correlation клацніть кнопку 2D scatterp (2-вимірні розсіяння).

У вікні Select two var. lists (horizontal and vertical vars in plots): виберіть у першому стовпчику змінну Надій, а у другому - % жиру і клацніть OK.

Буде побудовано графік лінійної залежності між змінними Надій і % жиру (пряма червона лінія) на фоні діаграми розсіяння (блакитні кружечки) (рис. 38).

Рис. 38. Графік залежності між змінними надій - % жиру

У заголовку вікна можна побачити рівняння знайденої лінійної залежності між змінними Надій і % жиру і точне значення коефіцієнту кореляції. Червоним пунктиром на графіку зображені межі 95%-ої зони довіри. У цій зоні знаходяться ті точки діаграми розсіяння, які з надійністю 0,95 (95%) описуються знайденою лінійною залежністю.

Збережіть графік лінійної залежності у свою робочу папку.

Занотуйте у робочий зошит процедуру побудови графіку лінійної кореляційної залежності між двома величинами.

Роздивіться уважно графік лінійної залежності і зробіть висновки, щодо характеру лінійної залежності між змінними Надій і % жиру. Занотуйте ці висновки у робочий зошит.

Порівняйте вигляд побудованого графіку лінійної залежності із діаграмою розсіяння, побудованою раніше (див.п.п.3-8) і визначте до яких років відносяться точки діаграми розсіяння, що знаходяться поза межами 95%-ої зони довіри. Занотуйте ці дані у робочий зошит. Зробіть висновки відповідно до мети даної роботи і занотуйте їх у робочий зошит. Закрийте всі відкриті вікна і закрийте програму STATISTICA.

Питання для самоконтролю

1. Що вивчає кореляційний аналіз?

2.Визначення парного, приватного, множинного

коефіцієнтів кореляції.

3. Як розраховується приватний коефіцієнт кореляції?

4. Як розраховується множинний коефіцієнт кореляції?

5.Як перевіряється значущість оцінки коефіцієнта парної

кореляції?

6.Як перевіряється значущість приватного коефіцієнта

кореляції?

7.Як перевіряється значущість множинного коефіцієнта

кореляції?

8. Для чого використовується коефіцієнт детермінації?

9. Як будується кореляційна матриця?

10.Як будуються довірчі інтервали для коефіцієнтів

кореляції?

Лабораторна робота 6

Проведення однофакторного дисперсійного аналізу

у системі STATISTICA

Мета роботи:

Навчитися процедурі проведення однофакторного дисперсійного аналізу у системі STATISTICA.

Зауваження. Мета дисперсійного аналізу – дати відповідь на питання: чи вірогідний вплив того чи іншого фактору на результати досліду (спостережень). Він також дає можливість порівняти між собою статистичні показники декількох статистичних рядів і визначити, чи є між ними статистично вірогідні відмінності і яка ймовірність цих відмінностей.

Для дисперсійного аналізу в англійській мові прийнято скорочення АNOVA/MАNOVA (Analys of Variances) – одно/многофакторний дисперсійний аналіз.

Завдання

Визначити вплив батьків (бугаїв – плідників – досліджуваний фактор (Х)). При цьому, бики є окремими градаціями цього фактору.

y_ij - кількість молочного жиру у дочок бугаїв, де індекс відповідає номеру бугая, jвказує порядковий номер доньки i –того бугая.

Кількість градацій фактору Х дорівнює 10.

В табл. 5. наведені значення жирномолочності дочок (y_ij), число лактацій дочок i-того бугая (n_i), сума продуктивності дочок i-го бугая (Y) і середнє значення продуктивності дочок i-того бугая (y_i = Y_i / n_i).

Початок роботи

1. У своїй робочій папці створіть нову папку Іаb6.

Всі файли, які буде створено при виконанні даної роботи, зберігайте у цій папці.

2. Створіть новий файл електронної таблиці для введення даних з табл.6.

Збережіть цей файл під назвою Іаb6.sta у свою робочу папку Іаb6

5.Кількість молочного жиру у корів (дочок бугаїв)

№ п.п.	Градації фактору (бугаї - плідники)
№ п.п.	В1	В2	В3	В4	В5	В6	В7	В8	В9	В10
1	120	152	130	149	110	157	119	150	144	159
2	155	144	138	107	142	107	158	135	112	105
3	131	147	123	143	124	146	140	150	123	103
4	130	103	135	133	109	133	108	125	121	105
5	140	131	138	139	154	104	154	104	132	144
6	140	102	152	102	135	119	188	150	144	129
7	142	102	159	103	118	107	156	140	132	119
8	146	150	128	110	116	138	145	103	129	100
9	130	159	137	103	150	147	150	132	103	115
10	152	132	144	138	148	152	124	128	140	146
11	115	102	154	135	138	124	100	122	106	108
12	146	160	165	132	115	142	170	154	152	119

Зауваження. Для дисперсійного аналізу дані вводяться особливим чином. Кожному варіанту досліду присвоюють свій код (номер варіанту). У першу змінну VAR1 вводяться коди варіантів, а у другу – VAR2 – спостереження значення результативної ознаки (кількість молочного жиру у дочок бугаїв) суворо по варіантах. Отже таблиця з даними повинна мати 2 стовпці (дві змінних) і 120 рядків (120 значень – 10 варіантів по 12 значень у кожному). Таблиця повинна мати наступний вигляд (табл.6):

6.Матриця дисперсійного комплексу

№ п.п.	Кількість молочного жиру
№ п.п.	1(Варіант)	2(Кількість)
1	1	120
…	…	…
12	1	146
…	….	…
13	2	152
…	…	…
15	2	160
…	…	…
25	3	130
…	..	…
27	3	128
…	…	…
37	4	149
38	4	107
39	4	143
…	…	…
49	5	110
47	5	142
48	5	124
…	…	…
61	6	157
62	6	107
63	6	146


73	7	119
74	7	158
75	7	140
…	…	…
85	8	150
86	8	135
87	8	150
…	…	…
97	9	…
98	9	…
99	9	…
	…	…
118	10	146
119	10	108
120	10	119

Послідовність проведення однофакторного аналізу

3. Переключіться до модуля і Breakdown & one-way ANQVA (Дисперсійний аналіз), виконавши команди:

Статистика > Основна статистика > Таблиці

4.У вікні Statistics by groups клацніть кнопку Variables введіть змінні для аналізу:

- у лівій колонці Independent variables (factors) (Незалежні змінні (фактори)) виділіть змінну Кількість;

- у правій колонці Dependent variable list (Список залежних змінних) виділіть змінну Варіант. Натиснуть OK.

Поверніться у вікно Statistics.

5. У вікні General ANOVA / MANOVA натисніть кнопку Codes for grouping variables (Коди для міжгрупових факторів), і у вікні Select codes for indep. vars (factors): (Bибip кодів для незалежних змінних (факторів)) натисніть кнопку All (Всі) тому, що необхідно провести дисперсійний аналіз всіх варіантів досліду. Натисніть ОК,

6. У вікні General ANOVA/MANOVA клацніть OK.

Відкриється вікно Statistics by groups - Results (Результати дисперсійного аналізу). У верхній частині вікна наведено назву залежної (DEPENDENT) змінної Кількість, назву змінної Бугаї плідники, яка містить номери кодів незалежних (факторних) змінних і коди варіантів 1 -10, що були включені до аналізу.

7. Щоб вивести результати дисперсійного аналізу у вікні Statistics by groups - Results натисніть кнопку Analysis of Variance.

Відкриється вікно, де міститься таблиця з розрахованими показниками.

8. Збережіть цю таблицю у свою робочу папку Іав6 у файлі з ім’ям anova_1.

9. Занотуйте розраховані показники дисперсійного аналізу у свій робочий зошит:

df Effect (Кількість ступенів вільності діючого фактору)__.

MS Effect (Середній квадрат діючого фактору)__________.

df Error (Кількість ступенів вільності для похибки) _____.

MS Error (Середній квадрат похибки) ________________.

F (Спостережене значення критерію Фішера) __________.

Р (Рівень довіри) ________

Зауваження. Рівень довіри - це кількість шансів на користь нульової гіпотези Н₀ про те, що між варіантами не має істотної (значущої) відмінності і, отже, фактор, що вивчається (бугаї плідники), не впливає на результативну ознаку (кількість молочного жиру у дочок).

Рівень довіри p-level - головне, що необхідно знати з цієї таблиці, щоб зробити висновок про наявність статистично достовірного впливу бугаїв на жирномолочність дочок. Якщо р - level < 0,05. то нульова гіпотеза Н₀ відкидається. В цьому випадку значення в таблиці подано червоним кольором. І тоді можна зробити висновок, що бугаї-плідники статистично достовірно впливають на кількість молочного жиру у дочок при рівні значущості 0,05. Якщо ж p - level > 0,05, то нульова гіпотеза Н₀ приймається. Значення в таблиці подаються чорним кольором, і можна зробити висновок, що бугаї-плідники статистично достовірно не впливають на кількість молочного жиру у дочок при рівні значущості 0,05.

За результатами дисперсійного аналізу зробіть висновок про наявність/відсутність статистично достовірного впливу бугаїв-плідників на кількість молочного жиру у дочок, і занотуйте висновок у робочий зошит.

Занотуйте процедуру однофакторного дисперсійного аналізу у робочий зошит.

Зауваження. Процедура дисперсійного аналізу, використана вище, спирається на F-критерій Фішера. Це один з параметричних критеріїв, використання яких передбачає, що дані спостережень мають нормальний розподіл. Тому, спочатку, перед використанням цієї процедури, необхідно було б перевірити нормальність розподілу дослідних даних. Для цього можна використати «нормальний» ймовірностний аркуш.

Апостеріорні порівняння середніх

Незалежно від сформульованого вище висновку, після одержання результатів дисперсійного аналізу необхідно продовжити вивчення діючого фактору і виконати попарне порівняння між собою всіх варіантів досліду (це називають порівнянням “a posteriori” (лат.: після досліду). У пакеті STATISTICA ця процедура має назву Post hoc comparisons (Пост-хок порівняння).

Відкрийте знов вікно statistis by groups Results та перейдіть на вкладинку Post hoc.

12. Натисніть кнопку Summary для розрахунку середніх значень по кожному з варіантів досліду. Збережіть результати розрахунків у свою робочу папку Іав6 у файлі з ім’ям seredni1.

13. Занотуйте у робочий зошит значення середніх по кожному з бугаїв-плідників:

VAR 1: Середнє =______кг молочного жиру у дочок;

Методичні вказівки розробили: 3

Коротков В.А- доцент кафедри розведення і генетики сільськогосподарських тварин кандидат с. – г. наук 3

Вступ 4

Лабораторна робота №1 Засвоєння інтерфейсу системи STATISTICA 5

Лабораторна робота №2 Первинна статистична обробка дослідних даних в системи STATISTICA 15

Лабораторна робота №3 Побудова діаграм і графіків у системі STATISTICA 22

Далі необхідно перевірити значущість відмінності між середніми.

Відкрийте знов вікно Statistics by groups – Results.

14. У вікні Statistics by groups - Results можна вибрати декілька апостеріорних критеріїв для перевірки значущості відмінності між середніми. Натисніть кнопку LSD test or planned comparison (Критерій НЗР найменшої значущої різниці. Еквівалентний t- критерію для незалежних вибірок). Відкриється вікно LSD test, де розраховано матрицю, елементами якої є розраховані рівні довіри для попарного порівняння середніх в усіх варіантах досліду.

15. Збережіть результати розрахунків у свою робочу папку Іав6 у файлі з ім’ям LSD_test.

Занотуйте у робочий зошит результати LSD-тесту (табл. 7).

16. За результатами LSD-тесту зробіть висновок про те, у яких варіантах досліду між середніми існує істотна (значуща) відмінність, і між якими середніми істотної відмінності немає (в залежності від значення рівня довіри). Занотуйте висновок у робочий зошит.

7.Рівень значущості відмінності між середніми (Р)

Варіанти досліду	1	2	3	4	5	6	7	8	9	10
1	-
2		-
3			-
4				-
5					-
6						-
7							-
8								-
9									-
10										-

17. Для того, щоб скористатися іншими критеріями для перевірки значущості відмінності між середніми, відкрийте знов вікно Statistics by groups - Results.

18. У вікні Post hoc Comparisons of Means клацніть кнопку Sheffe test (Критерій Шеффе). Критерій Шеффе використовують у найбільш відповідальних випадках.

Відкриється вікно Sheffe test.

Збережіть результати розрахунків у свою робочу папку Іаb6 у файлі з ім’ям Sheffe.

Занотуйте у робочий зошит результати Sheffe-тесту (табл.8).

8.Рівень значущості відмінності між середніми (Р)

Варіанти досліду	1	2	3	4	5	6	7	8	9	10
1	-
2		-
3			-
4				-
5					-
6						-
7							-
8								-
9									-

14. За результатами Sheffe-тесту зробіть висновок про те, у яких варіантах досліду між середніми існує істотна (значуща) відмінність, і між якими середніми істотної відмінності не має.

Занотуйте висновок у робочий зошит.

15. Пакет STATISTICA дозволяє оцінити відмінність між різними варіантами досліду шляхом перевірки нульової гіпотези про те, що різниця між середніми різних варіантів досліду дорівнює нулю. Для цього використовують критерій Дункана (Duncan’s test).

Перед використанням критерію Дункана розрахуйте вручну різниці (кроки) між середніми варіантів досліду:

Крок1: Середнє1 - Середнє2 = _____

Крок2: Середнє1 - СереднєЗ = _____

16. Натисніть кнопку Duncan’s multiple range test & critical ranges (Критерій Дункана і критичні розмахи).

Відкриється два вікна: перше вікно Duncan test, де розраховано матрицю, елементами якої є розраховані рівні довіри щодо нульової гіпотези про рівність нулю різниць між середніми різних варіантів досліду, і друге вікно Duncan test, у якому розраховані критичні значення кроків (Step 1 і Step 2) між середніми, менше яких відмінність між середніми при рівні довіри 0,05 можна вважати неістотною (незначущою). Занотуйте у робочий зошит результати Duncan-тесту (з першого вікна):

9.Рівень значущості відмінності між середніми (Р)

Варіанти досліду	1	2	3	4	5	6	7	8	9	10
1	-
2		-
3			-
4				-
5					-
6						-
7							-
8								-
9									-
10										-

Критичні кроки (з другого вікна):

Step 1 =______.

Step 2 =______.

…..

17. За результатами Duncan-тесту зробіть висновок про те у яких варіантах досліду між середніми існує істотна (значуща) відмінність, і між якими середніми істотної відмінності не має. Занотуйте висновок у робочий зошит.

Занотуйте у робочий зошит процедуру пост-хок порівняння.

18. Зробіть узагальнюючий висновок за результатами апостеріорних порівнянь. Занотуйте висновок у робочий зошит.

Висновок може бути таким:

Бугаї – плідники (батьки корів) статистично істотно впливають на жирномолочність дочок. Максимальна кількість жиру в молоці корів встановлена у бугаїв В , В , В Встановлені показники статистично вірогідно відрізняються від аналогічних показників отриманих від доньок бугаїв В , В , В . По іншим бугаями відмінностей по фенотиповому різноманіттю кількості жиру в молоці дочок виявились статистично невірогідними.

Графічне порівняння варіантів досліду

Відмінність між варіантами досліду можна легко побачити за допомогою графіків типу “ящик з вусами”.

19. Відкрийте знов вікно Statistics by groups - Results та перейдіть на вкладнику Descriptives.

20. Клацніть кнопку Categorized box & whisker (Описові статистики і графіки). Відкриється вікно Box -Whisker Туре.

21. У вікні Box-Whisker Туре виберіть “ящик з вусами” типу Median/Quart./Range (Медіана/Квартилі/Розмах) і клацніть ОК.

Відкриється вікно з побудованим графіком.

Уважно розгляньте і попарно порівняйте між собою графіки для варіантів 1, 9. За результатами візуального порівняння графіків зробіть висновок про те, середні яких варіантів досліду відрізняються істотно або неістотно. Занотуйте висновок у робочий зошит.

Завершення роботи

Закрийте всі відкриті вікна і вимкніть програму STATISTICA.

Питання для самоконтролю

1. У чому полягає мета дисперсійного аналізу?

2. Вказати дві умови, які повинні виконуватися для проведення дисперсійного аналізу.

3. Навести формулу розрахунку впливу фактора.

4. Вказати назву модуля з проведення дисперсійного аналізу.

5. Вказати різницю між тестами LSD, Sheffe та Duncan.

Лабораторна робота №7

Проведення двофакторного дисперсійного аналізу

у системі STATISTICA

Мета роботи:

Вивчити процедуру проведення двофакторного дисперсійного аналізу у системі STATISTICA.

Зауваження. Принципові основи двофакторного дисперсійного аналізу є такі ж самі, як і в однофакторному дисперсійному аналізі. Підсумком двофакторного дисперсійного аналізу є оцінка дії не тільки кожного з факторів, що вивчаються, на результативну ознаку, але й оцінка їх взаємної дії на цю ознаку. Під час виконання даної роботи буде обчислено критерій Фішера й рівень його статистичної значущості для нульової гіпотези про відсутність дії кожного з факторів, що вивчаються. Нульова гіпотеза звичайно відкидається, і фактор вважається статистично вірогідно діючим при Р < 0,05. Додатково буде обчислено силу впливу кожного з факторів окремо та разом і виявлено за допомогою критерію Шеффе чи інших (Дункана, LSD) варіанти досліду, які вірогідно відрізняються один від одного.

Завдання

У досліді вивчалась дія стимулятора на плодючість маток при різній повноцінності раціонів годівлі.

Повноцінність раціону (першій фактор) надана двома градаціями:

А1-раціон не збалансований за мінеральними

речовинами;

А2-раціон збалансований за усіма поживними

речовинами ( у тому числі і мінеральними).

Стимулятор (другий фактор) вивчалася у трьох варіантах (дозах):

Д1- одинарна доза;

Д2- подвійна доза;

Д3- потрійна доза.

Результативною ознакою була плодючість маток (кількість тварин в пометі, при народженні).

Повторність досліду була трикратною.

Для кожного поєднання градацій раціону і дози стимулятора відібрали по методу аналогів три матки.

Результати дослідів наведені у таблиці 10.

Провести двофакторний дисперсійний аналіз з метою визначення наявності статистично достовірного впливу поживності раціону і дози стимулятора на плодючість маток

10.Двофакторний рівномірний дисперсійний комплекс

Раціони (А)	А1			А2
Дози стимулятора (Д)	Д1	Д2	Д3	Д1	Д2	Д3
Плодючість, гол.	5	4	2	1	10	7
	6	3	3	4	9	4
	7	5	1	1	11	7

Початок роботи

1. У своїй робочій папці створіть нову папку 1аb7. Всі файли, які буде створено при виконанні даної роботи, зберігайте у цій папці.

2. Запустіть програму STATISTICA і у модулі Data Management/MFM створіть новий файл електронної таблиці для введення даних (з табл. 10). Збережіть цей файл під назвою Iab8.sta у свою робочу папку 1аb7.

Зауваження. У змінні VAR1 (Раціон) і VAR2 (Доза стимулятора) будемо вводити, відповідно дані про збалансованість раціону та дози фактора, а у третю змінну - VAR3 - спостережені значення результативної ознаки - дані про плодючість маток. Значення змінних запишемо у нову таблицю таким чином: раціон А1, А2, доза стимулятора Д1, Д2,Д3.

Отже, таблиця з даними повинна мати 3 стовпці (три змінних) і 18 рядків (18 значень - 3 варіанти досліду по 6 значенням у кожному).

Електронна таблиця повинна мати наступний вигляд (табл.11) (рис 39).

11.Від трансформованої таблиці 10

№ Пп	Дослідження плодючості свиноматок
№ Пп	1 (Раціон)	2 (Доза стимулятора.	3 Плодючість
1	А1	Д1	5 6
2	А1	Д1	6
3	А1	Д1	7
4	А1	Д2	4
5	А1	Д2	3
6	А1	Д2	5
7	А1	Д3	2
8	А1	Д3	3
9	А1	Д3	1
10	А2	Д1	1
11	А2	Д1	4
12	А2	Д1	1
13	А2	Д2	10
14	А2	Д2	9 1
15	А2	Д2	11
16	А2	Д3	7
17	А2	Д3	4
18	А2	Д3	7

Рис. 39. Електронна таблиця

Уважно розберіться в її структурі: перші дві змінні призначені для запису варіантів, в третій-записані облікові дані продуктивності у строгій відповідності до змісту варіантів.

Виконання двофакторного дисперсійного аналізу

3. Виконайте команди Статистика → Аналіз варіантів на панелі інструментів викличте вікно STATISTICA Module Switcher і переключіться до модуля ANOVA/MANOVA (Однофакторний / Багатофакторний дисперсійний аналіз).

4. У вікні General ANOVA/MANOVA (Загальний дисперсійний аналіз) переконайтесь в тому, що у полі Type of

analysis вибраний пункт Factorial ANOVA, а у полі Specification method - пункт Quick specs dialog ОК.

5. У вікні ANOVA/MANOVA Factorial ANOVA клацніть кнопку Variables і вкажіть змінні для аналізу наступним чином:

У лівій колонці Dependent variable list: (Список залежних змінних) виділіть змінну Плодючість.

У правій колонці Categorical predictors (factors): (Незалежні змінні (фактори) виділіть змінні Раціон та Доза стимулятора і натиснуть ОК.

Повернетесь у вікно General ANOVA/MANOVA.

6. У вікні General ANOVA/MANOVA клацніть кнопку Factor codes: (коди для між групових факторів), і у вікні Select codes for indep. vars (factors): (Вибір кодів для незалежних змінних (факторів): клацніть кнопку Select All (Вибрати всі), бо необхідно провести дисперсійний аналіз всіх варіантів досліду. ОК.

7. У вікні General ANOVA/MANOVA клацніть OK.

Відкриється вікно ANOVA Results 1 (Результати дисперсійного аналізу).

8. Щоб вивести результати дисперсійного аналізу, у вікні ANOVA Results клацніть кнопку All effects (Всі ефекти).

Відкриється вікно Summary of all Effects (Підсумок всіх показників), де міститься таблиця з розрахованими показниками дисперсійного аналізу.

9. Збережіть цю таблицю у свою робочу папку lab7.

10.Занотуйте показники дисперсійного аналізу що описують окремо вплив /рівня годівлі, вплив дози стимулятора /, а також одночасний вплив цих чинників у свій робочий зошит.

11. За результатами дисперсійного аналізу зробіть висновок щодо того, чи є статистично достовірним вплив рівня годівлі та використання стимулятора, а також поєднання цих чинників на плодючість маток, і запишіть цей висновок у свій робочий зошит.

12.Занотуйте процедуру проведення двофакторного дисперсійного аналізу у свій робочий зошит.

Апостеріорні порівняння середніх

Для більш поглибленого аналізу результатів виконаємо попарне порівняння між собою всіх варіантів досліду як для кожного з чинників окремо, так і для випадку їх взаємодії. При цьому слід пам’ятати, що Post hoc порівняння робляться окремо для кожного із чинників і для їх поєднання. Тому кожен раз для здійснення процедури порівняння необхідно повертатись до вікна Specify Effect for Post hoc Tests (Завдання діючих факторів для пост - хок тестів). Так, спочатку необхідно проаналізувати змінну Раціон, - потім - Доза, і, нарешті, виділивши обидві змінні (Рацион, Доза), і випадок їх одночасної дії.

13. Клацніть кнопку Continue... у вікні Summary of all Effects і, повернувшись у вікно ANOVA Results, клацніть кнопку Summary та кнопку Cell statistics. Відкриється вікно Descriptive Statistics.

14. У вікні Descriptive Statistics розраховані середні значення (Means) по кожному з варіантів досліду:

Раціон А2 Means = 6.

Раціон А1 Means = 4.

Доза стимулятора 1 Means = 4.

Доза стимулятора 2 Means = 7.

Доза стимулятора 3 Means = 4.

Раціон А2 Доза стимулятора Д1 Means = 1,7.

Раціон А2 Доза стимулятора Д2 Means = 6,7.

Раціон А2 Доза стимулятора Д3 Means = 6.

Раціон А1 Доза стимулятора Д1 Means = 6.

Раціон А1 Доза стимулятора Д2 Means = 4.

Раціон А1 Доза стимулятора Д3 Means = 2.

Бачимо, що різниця між середньою плодючістю маток при годівлі за раціоном А1 і А2 є, але у випадку використання стимулятора плодючість виявляється набагато вищою, ніж без стимулятора.

Якщо визначити одразу обидві змінні, то буде помітний такий порівняльний результат:

Раціон А1 доза стимулятора Д1 Means = 6

Раціон А1 доза Д2 Means = 4.

Раціон А1 доза Д3 Means = 2.

Раціон А2 доза Д1 Means = 2.

Раціон А2 доза Д2 Means = 10.

Раціон А2 доза Д3 Means = 6.

Перевіримо значущість відмінності між середніми.

15. Поверніться у вікно ANOVA Results, клацніть кнопку More results Statistics та перейдіть на вкладнику Post hoc.

16. Виберіть у списку Effect змінну Раціон і клацніть кнопку Fisher LSD (Критерій НЗР – найменшої значущої різниці).

Відкриється вікно LSD Test, де подано матрицю, елементами якої є розраховані рівні довіри для попарного порівняння середніх в усіх варіантах досліду.

Занотуйте у робочий зошит результати LSD - тесту.

17. Поверніться у вікно ANOVA Results і, аналогічно, вибираючи послідовно спочатку змінну Доза, а потім одночасно змінні Раціон * Доза, отримайте результати розрахунків для всіх варіантів досліду.

18. За результатами LSD - тесту зробіть висновок про те, у яких варіантах досліду між середніми існує істотна (значуща) відмінність, і між якими середніми істотної відмінності немає.

Занотуйте цей висновок у робочий зошит.

Використаємо інші критерії для перевірки значущості відмінності між середніми. Для цього клацніть кнопку Continue...OK.

19. Вибираючи послідовно у вікні Доза змінні Раціон, Доза, а потім Раціон і Доза одночасно, у вікні ANOVA Results клацніть кнопку Sheffe test (Критерій Шеффе). Як відомо, критерій Шеффе використовують у найбільш відповідальних випадках.

Відкриється вікно Sheffe test.

Тест Шефе покаже, що статистично достовірна лише різниця варіантів з стимуляторами та без них, годівлі та поєднання годівлі з використанням стимулятора у всіх випадках не дали статистично достовірного ефекту.

Занотуйте у робочий зошит результати Sheffe-тесту.

20. За результатами Sheffe - тесту зробіть висновок про те, у яких варіантах досліду між середніми існує істотна (значуща) відмінність, і між якими середніми істотної відмінності немає.

21. Використовуючи критерій Дункана (Dunkan’s test), проведемо оцінку відмінності між різними варіантами досліду шляхом перевірки нульової гіпотези про те, що різниця між середніми різних варіантів досліду дорівнює нулю.

Вибирайте у вікні ANOVA Results послідовно спочатку змінні Раціон, Доза , а потім Раціон*Доза одночасно.

Розрахуйте вручну різниці між середніми варіантів досліду для всіх комбінацій змінних та запишіть їх у зошит.

22. Клацніть кнопку Duncan’s. Переконайтесь в тому, що при рівні довіри 0,05 відмінність між середніми є істотною лише для випадків З дозою стимулятора Д1 …– Д3.

Силу впливу факторів доводиться дораховувати на калькуляторі, використовуючи дані дисперсійного аналізу. Вона дорівнює (табл. 12):

ή _{раціон
(А)} = (18 / 158) × 100 = 11%;

ή _стим(В) = (36 / 158) × 100 = 23%;

ή _{раціон.стим(АВ)} = (84 / 158) × 100 = 53%;

ή _{орган факт} = (138 / 158) × 100 = 0,87;

ή _{випадкове} = (20 / 158) × 100 = 13%.

Загальні результати двофакторного дисперсійного аналізу оформіть у вигляді таблиці 12.

В результаті проведених досліджень встановлено, що усі факторіальні впливи виявились статистично вірогідними.

Сила впливу фактора А (рівень годівлі) складає 10,8%.

Сила впливу фактора В (доза стимулятора) складає 23%.

Сила впливу діючих факторів А,В (рівня годівлі та дози стимулятора) складає 53%.

12.Результати аналізу двофакторного дисперсійного комплексу

Джерела змін	Дисперсія (С)	Ступені свободи (γ)	Варіанси (σ_і²)	Критерій Фішера (F)	Рівень довіри (Р)
Годівля	18	1	18	10,8	>0,99
Доза стимул.	36	2	18	10,8	>0,99
Годівля-стимул.	84	2	42	25,2	>0,999
Організованих факторів	138	5	27,6	16,5	>0,999
Випадкове	20	12	1,67	-	-
Загальне	158	17	-	-	-

Для дослідного комплексу характерна висока доля впливу організованих факторів (ή_х= 0,87). Це означає, що стимулятор плодовитості і повноцінність раціону виявляли в значній степені то різновид плодовитості, яке спостерігалось в дослідній групі маток. Це позначилося і в малій долі впливу неорганізованих факторів (ή_z = 0,13), тобто разом 13% від впливу усіх факторів.

Збережіть результати розрахунків з усіх вікон у свою робочу папку.

Зробіть технологічний висновок за результатами досліду.

Проведені дослідження дозволяють зробити слідуючи висновки відносно дій стимулятора при його масовому використанні.

1. Стимулятор при його масовому використанні буде підвищувати плодовитість маток тільки в його відповідності з повноцінним раціоном (рівень вірогідності Р > 0,999).

2. Найбільш відповідну дію показує двійна доза стимулятора при повноцінних раціонах (Р > 0,999).

3. При недостатності в кормі мінеральних сполук двохкратні і трьохкратні дози стимулятора можуть навіть знизити плодовитість маток (Р > 0,99).

Графічне порівняння варіантів досліду

Відмінність між варіантами досліду можна легко побачити за допомогою графіків типу "ящик з вусами".

23. У вікні ANOVA Results перейдіть на вкладинку Means та, послідовно вибираючи у списку Plot or show means for effect: (графік або розрахунок середніх для змінної) спочатку Раціон, Доза, а потім Раціон * Доза, побудуйте графіки для всіх комбінацій змінних.

За результатами візуального порівняння графіків зробіть висновок про те, середні яких варіантів досліду відрізняються істотно або неістотно.

Занотуйте висновок у робочий зошит.

Закрийте всі відкриті вікна і вимкніть програму STATISTICA.

Питання для самоконтролю

1. Призначення двофакторного дисперсійного аналізу?

2. У чому полягають особливості проведення двофакторного дисперсійного аналізу в системі STATISTICA.

3. Які задачі можливо рішать дисперсійним аналізом?

4. Навести критерії для перевірки значущості відмінності між середніми.

Лабораторна робота №8

Проведення простого лінійного регресійного аналізу у системі STATISTICA

Мета роботи:

Вивчити процедуру проведення лінійного регресійного аналізу у системі STATISTICA.

Зауваження. Мета регресійного аналізу - з’ясувати ступінь впливу тих або інших діючих факторів на результативні кількісні ознаки тварин. Наприклад, саме так звичайно вивчається дія інтенсивності росту на скоростиглість свиней тощо. При регресійному аналізі встановлюють, як змінюється відгук (значення результативної ознаки) по мірі наростання середньодобового приросту - фактору, наскільки значні ці зміни і який ступінь їх статистичної вірогідності. Самі по собі відгуки для наочності і більш правильного аналізу звичайно зображають графічно. У підсумку лінійного регресійного аналізу одержують аналітичний вираз для прямої лінії регресії з визначенням коефіцієнтів рівняння регресії, а також графічне зображення лінії регресії.

Загальна модель простої однофакторної регресії має вид:

у = f(x) + е,

де у - відгук,

х - діючий фактор,

е - випадкова помилка, що описує дію факторів, не врахованих у досліді. При лінійній однофакторній регресії її аналітичний вираз має вид:

у = b₀ + b₁x + е,

Завдання регресійного аналізу - знайти коефіцієнти цього виразу, після чого регресійна модель повинна бути перевірена методом дисперсійного аналізу при нульовій гіпотезі Но: b₁ = 0, яка полягає в тому, що дія факторної ознаки на результативну ознаку відсутня.

Завдання

У свиней з різною скоростиглістю визначили середньодобовий приріст. Одержані дані були занесені в таблицю. Провести лінійний регресійний аналіз отриманих експериментальних даних.

Початок роботи

1. У своїй робочій папці створіть нову папку 1аb8. Всі файли, які буде створено при виконанні даної роботи, зберігайте у цій папці.

2. Створіть новий файл електронної таблиці для введення даних (з табл. 13).

13.Показники продуктивності свиней

№ п.п.	Середньодобовий приріст, г	Вік досягнення маси 100кг, діб.
1	460	212
2	490	202
3	370	230
4	515	196
5	510	187
6	360	227
7	440	218
8	380	225
9	360	231
10	560	178

Збережіть цей файл під назвою Iab8.sta у свою робочу папку 1аb8.

Зауваження. У першу будемо вводити середньодобовий

приріст, а у другу - вік досягнення маси 100кг.

3 Shape1 . Виконайте команди Статистика Множественная регрессия. Регресійний аналіз у системі STATISTICA розпочинається з перевірки нульової гіпотези про відсутність впливу факторної ознаки на результативну.

4. У вікні Multiple Linear Regression (Множинна лінійна регресія) клацніть кнопку Variables і введіть змінні для аналізу наступним чином:

у лівій колонці Dependent variables: (Вік досягнення маси 100кг) виділіть змінну VAR2;

у правій колонці Independent variables: (Незалежні змінні:) виділіть змінну середньодобовий приріст VAR1 (рис.40).

Поверніться-у вікно Multiple Regression. - OK

5.Відкриється вікно Multiple Regression Results з результатами регресійного аналізу (рис. 41).

Рис.40. Відбір змінних для лінійного регресійного аналізу

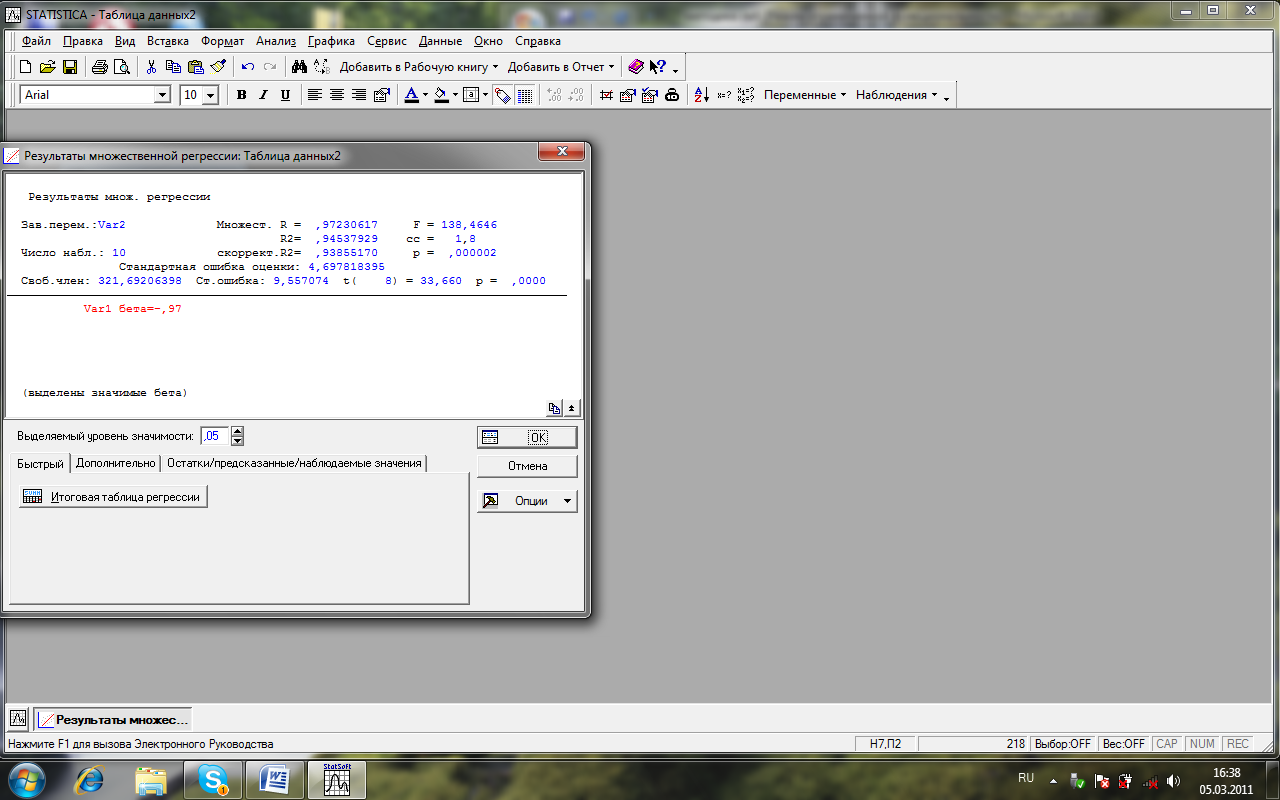
Рис. 41. Результати проведення регресійного аналізу

Випишіть у робочий зошит розраховані показники дисперсійного аналізу у вигляді (Advanced а Sammary Regression results): R = ___________.

F = ___________.

df = ___________.

p = ____________.

Як бачимо, на користь нульової гіпотези b₁=0 зовсім мало шансів (це випливає з того, що значення Р дуже мале, менше 0,05), отже, лінійна регресія статистично достовірна на рівні 95%.

6. У вікні Multiple Regression Results випишіть:

R² = _________.

Це коефіцієнт детермінації. Загальний розкид тут приймається за 1,0 і R показує частину цього розкиду, враховану регресією. Вона становить 93%, що означає: на частку випадкових факторів, не врахованих регресією, залишилось лише 7%. Це добрий результат.

7. Натисніть кнопку Summary: Regression results. У стовпці "В" наведене значення вільного члена рівняння регресії (intercept) (рис.42 ).

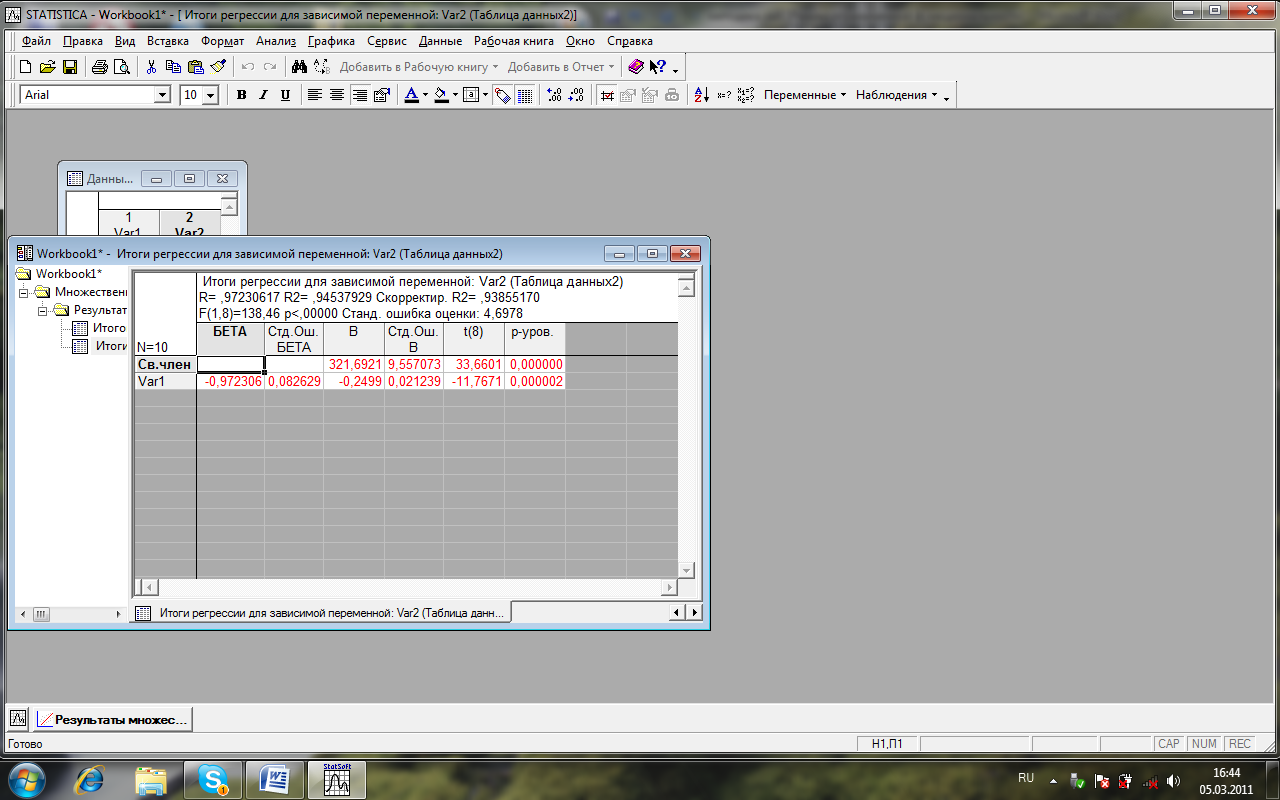
Рис. 42. Параметри рівняння регресії

Випишіть це значення у робочий зошит:

b₀=_________

Із стовпчика Р видно, що шансів на користь нульової гіпотези про те. що b₀ дорівнює нулю, всього ________. Отже, цей коефіцієнт статистично достовірний.

На перетині стовпчика "В" і змінної середньодобовий приріст - знаходиться коефіцієнт b₁. Випишіть його значення у зошит:

b₁=( ) (при Р = 0, )

цей коефіцієнт також статистично достовірний. Отже рівняння регресії в цілому статистично достовірно. Можемо записати рівняння регресії у такому вигляді:

Вік досягнення 100кг, діб. = b₀ + b1×Середньодобовий приріст, г.

Запишіть це рівняння у зошит.

Аналіз залишків

Залишками називають різницю між спостереженими значеннями результативної ознаки та теоретичними значеннями її, розрахованими за рівнянням регресії.

8. У вікні Multiple Regression Results перейдіть на вкладнику Residuals/assumptions/prediction та натисніть клавішу Perform residual analysis (аналіз залишків), а потім кнопку Summay: Residuals & predicted (показати залишки і передбачені значення).

В таблиці, що відкрилась, в графі Predicted Value (прогнозовані значення) наведені значення віку досягнення 100кг (діб), що точно відповідають тому чи іншому середньодобовому приросту( г) /.

Це ті точки, що лежать точно на прямій лінії регресії.

Поверніться у попереднє вікно.

9. Результати регресійного аналізу необхідно подати у вигляді графіка (рис. 43). Для цього натисніть клавішу Normal plot of residuals.

На цьому графіку показана лінія регресії та точки, що відповідають дослідним даним.

Закрийте всі відкриті вікна і вимкніть програму STATISTICA.

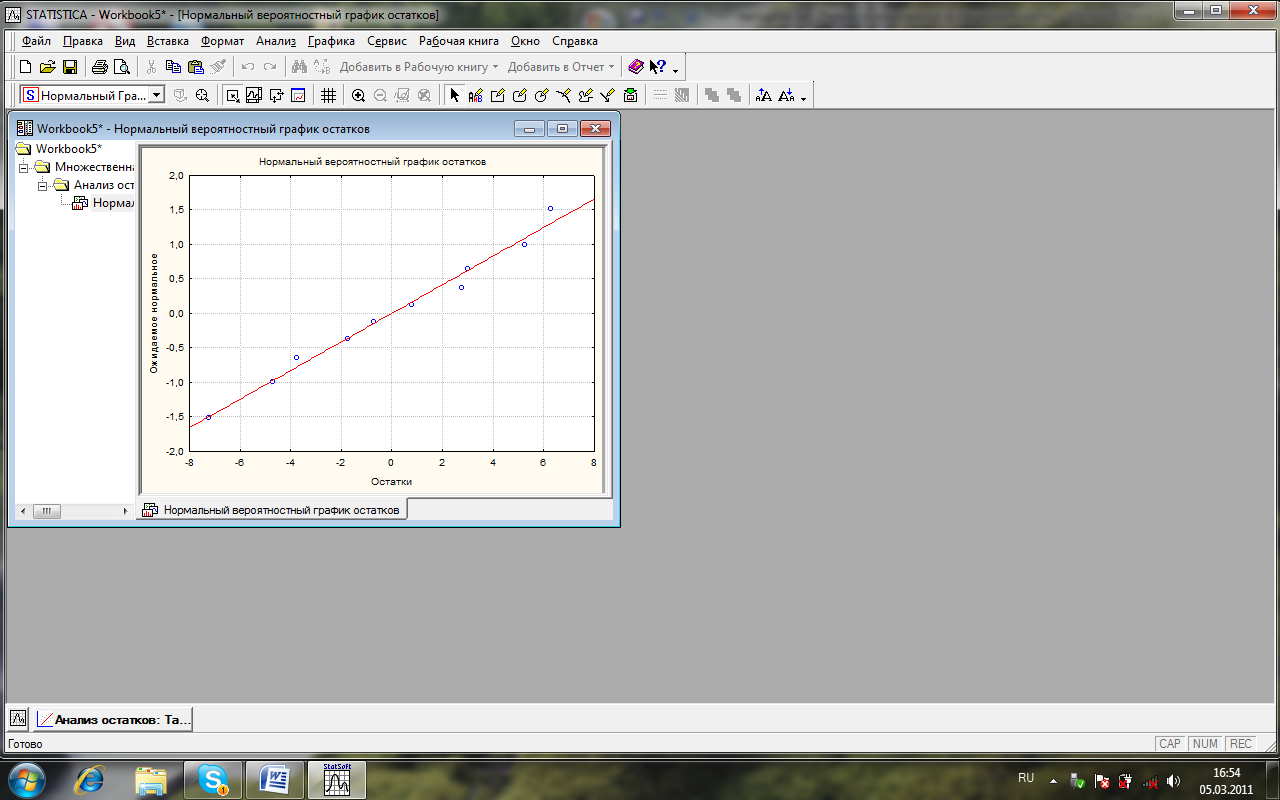
Рис. 43. Графік лінії регресії

Множинний регресійний аналіз в системі STATISTICA

Зауваження. Лінійна модель з декількома предикаторами називається лінійною множинною регресійною моделлю, а саме:

Yi, = b₁x₁_i + b₂,х₂ + + bp + bp_i +b₀+ с,

де b₀, b₁,b₂, .., bр – невідомі параметри моделі, які розраховуються за допомогою систем нормальних рівнянь. Наприклад, система нормальних рівнянь для регресії з двома предикаторами має наступний вигляд:

n Shape2 b₀ + b₁_iх₁_i + b₂∑_ix₂_i = ∑_iy_i

b₀ ∑_ix₁_i x₁_i² + b₂_iх₂_i + b₂ ∑_ix₁_i x₂_i = ∑_ix₁_i y_i

b_o ∑_ix₂_i + b₁∑_ix₁_ix₂_i + b₂ ∑_ix₂_i² = ∑_ix₂_i y_i

Завдання

Вивчалась річна динаміка об’ємів реалізації продукції (молока) по господарствах району. При цьому прийняті до уваги наступні показники:

- об’єм продаж продукції за поточний місяць (Var 1);

- об’єм продаж продукції за попередній місяць (Var 2);

- надбавка за продукцію в поточному місяці (Var 3);

- надбавка за продукцію в попередньому місяці (Var 4);

- кількість корів у господарстві (Var 5);

- середня кислотність молока (Var 6);

- індекс роздрібних цін в поточному місяці (Var 7).

Одержані дані занесені в таблицю.

Провести лінійний регресійний аналіз отриманих даних.

Початок роботи

1.У своїй робочій папці створіть нову папку 1аb9. Всі файли, які буде створено при виконанні даної роботи, зберігайте у цій папці.

2.Створіть новий файл електронної таблиці для введення даних (з табл. 14)

Міс. року	Var1	Var2	Var3	Var4	Var5	Var6	Var7
1	8846,4	10132	288,5	200	1675	8,2	101,5
2	8774,7	8846,4	324,2	288,5	1405	9,4	103,8
3	9524,7	8774,7	332,2	324,2	723	15,1	109,2
4	11134,3	9524,7	439,2	332,2	2230	20,9	108,9
5	12239,8	11134,3	98,2	439,2	2615	25,7	112,4
6	8862,1	12239,8	212,8	98,2	3089	26,3	113,1
7	8646,9	8862,1	416	212,8	1741	22,8	114,1
8	11758,5	8646,9	327,7	416	2060	18,7	116
9	11867,2	11758,5	160,6	327,7	1777	15,5	116,6
10	9577,6	11867,2	403,1	160,6	1378,9	11,7	133,6
11	10898,4	9577,6	269,7	403,1	1253,3	5,6	119,5
12	9638,6	10898,4	280,5	269,7	794	6,5	130,6
13	9203,9	9638,6	335,1	280,5	1384,4	8,1	125
14	9231,1	9203,9	169,3	335,1	1392,5	10,3	124,2
15	7334,5	9231,1	206	169,3	2484,4	9,7	130,7
16	7647	7334,5	216,1	206	2777,5	22,4	131,6
17	7839,6	7647	322,2	216,1	3301,9	20,6	133,4
18	9787	7839,6	285,5	322,2	3636	26,8	139,1
19	9600	9787	79,2	285,5	3415	27,8	142,3
20	7199,9	9600	333,6	79,2	2606	18,3	139,9
21	9547,7	7199,9	293,1	333,6	2508	12	144,5
22	10187,5	9547,7	238,5	293,1	2834,1	9,7	143,9
23	9661,2	10187,5	255,4	238,5	2481	5,1	148
24	9189,2	9661,2	383,6	255,4	1474,4	2,8	149,3

3.Збережіть цей файл під назвою Iab9.sta у свою робочу папку 1аb9.

14.Динаміка об’ємів продажі молока по господарствах

4. Запустити множинний регресійний аналіз шляхом вибору модулю «Множественная регрессия - Multiple Linear Regression» у вікні «Анализ»и натискання кнопки ОК (рис.44).

Рис.44. Відбір модуля «Множественная регрессия Multiple Linear Regression»

5 Shape3 .У вікні Multiple Linear Regression (Множинна лінійна регресія) клацніть кнопку Variables і введіть змінні для аналізу наступним чином:

у лівій колонці Dependent variables: (Залежні змінні:)

виділіть змінну VAR1;

у правій колонці Independent variables: (Незалежні змінні:) виділіть змінні VAR2…- VAR7 (рис. 45).

Рис.45 Відбір залежних та незалежних змінних

6.Відкриється вікно Multiple Regression Results з результатами регресійного аналізу (рис. 46).

Рис.46. Вікно результатів проведення множинного регресійного аналізу

7. Випишіть у робочий зошит розраховані показники дисперсійного аналізу у вигляді:

R = _________.

F = _________.

df = ________.

p = _________.

R² = ________.

Натисніть кнопку «Cаncel» и изменить процедуру на пошаговую «Advenced options Stepwise or ridge regression» (Пошаговая или гребневая регрессия).

Виберіть метод на вкладинці «Advenced» (рис. 57).

Рис.47. Вікно множинної регресії

Виберіть параметри пошагової процедури (рис. 48) і натисніть ОК.

Рис.48.Вікно відбору методу пошагового аналізу

Рис. 49. Вибір методу

Рис.50. Вікно параметрів процедури пошагової регресії

Отримати результати аналізу у вигляді таблиці (рис.51).

Натисніть кнопку «Summary: Regression results.» на вкладниці «Advаnced» (рис. 52 ).

Висновки викладені в вигляді таблиці.

Рис. 51. Результат стандартної регресії

Верніться в вікно аналізу натиснувши кнопку «Multiple Regression Resalt».

Провести аналіз залишків, натиснувши кнопку «Perform residual analysis» на вкладниці Residuals/assumptions/ prediction».

Результат викладений у вигляді таблиці.

Рис. 52.Аналіз залежності між залишками і прогнозом

Досліджувати залежність між залишками і прогнозом натиснувши на кнопку «Durbin- Watson statistic» на вкладке «Advenced». Результати будуть викладені в таблиці(рис.53).

Рис.53. Результати статистики Дарбіна Уотсона

Повернутись в вікно аналізу, натиснувши на кнопку «Residual/ assumption/pre….» (рис.54).

Натиснути кнопку «Predicted vs/ Observed».

Результати будут представлени в таблиці (рис.55).

Повернутися до вікна аналізу, натиснувши кнопку «Residual Analysis ….»

Рис. 54. Результат пошагової регресії

Натиснути на кнопку «Cаncel» для повернення в вікно «Model definition» (рис.55). ОК.

Натиснути кнопку «Predict dependent variable» на вкладниці «Residuals/assumptions/prediction».

Рис.55. Вікно «Model definition»

Ввести дані для прогнозу на наступний місяць (рис.56) і натиснути кнопку ОК.

Рис.56. Введення даних для прогнозу на наступний місяць

Рис.57. Вікно результатів прогнозу

Рис. 58. Параметри покрокової процедури

Рис.59. Вікно підсумків покрокової регресії

Рис.60. Вікно аналіз залишків

Рис. 61. Спостережні і прогнозовані значення

На цьому графіку показана лінія регресії та точки, що відповідають дослідним даним.

Закрийте всі відкриті вікна і вимкніть програму STATISTICA.

Питання для самоконтролю

1. Мета проведення регресійного аналізу?

2. В чому полягає перевірка значущість парної регресійної

моделі?

3. Як перевіряється значущість регресорів в множинному

аналізі?

4. Як оцінюються коефіцієнти регресії?

5. Як перевіряється значущість рівняння регресії?

6. Як перевіряється значущість коефіцієнтів регресії?

7. Як будуються інтервальні оцінки коефіцієнтів

рівняння регресії?

Лабораторна робота №9

Проведення кластерного аналізу у системі STATISTICA

Мета роботи:

Вивчити процедуру проведення кластерного аналізу у системі STATISTICA.

Зауваження. Кластерний аналіз розв’язує задачі групування і класифікації об’єктів одразу за кількома ознаками. В підсумку кластерного аналізу розраховуються значення відстаней між об’єктами в уявному багатовимірному просторі, координатами якого є значення ознак, що враховуються під час досліду, і будуються спеціальні графіки - дендрограми, які наочно показують, наскільки близькі між собою об’єкти, що досліджуються, відразу за всією сукупністю їх властивостей, що були враховані у досліді.

Для вирішення задач в кластерному аналізі використовуються наступні методи: Joining (tree clustering) (ієрархічні агломеративні методи або деревовидна кластеризація), K - means clustering (метод К середніх), Two-way joining (двовхідне о`бєднання).

Кластерний аналіз має велике значення для використання в селекційній роботі, знаходить широке застосування при класифікації генотипів тварин.

Завдання

Під час дослідної роботи отримані і занесені в таблицю характеристики шести основних порід свиней за шістьма показниками хімічного складу м’язової тканини:

гігроскопічна волога, %;.
попіл, %;
протеїн, %;
клітковина, %;
жир, %;
безазотисті екстрактивні речовини, %.

За допомогою кластерного аналізу оцініть подібність наведених порід свиней одразу за всіма шістьма ознаками.

Дослідні дані наведені в таблиці 15.

15.Хімічний склад м’язової тканини свиней

Порода свиней	VAR 1	VAR 2	VAR 3	VAR 4	VAR 5	VAR 6
Велика біла Пшениця яра	13,4	1,9	13,6	1.8	2,0	67,3
Миргородська	13,4	1,8	11,4	1,8	1,9	69,7
Полтавська м’ясна	15,1	1,7	11,5	2,1	1,8	67,8
Ландрас	12,4	2,6	12,3	4,5	2,5	65,8
Українська степова біла	12,8	3,0	10,2	10,0	5,3	59,7
Велика чорна Кукурудза	13,3	1,5	9,6	2,6	5,1	67,9

Розглянемо принцип проведення кластерного аналізу на основі даних, які наведені в таблиці 15. В файлі знаходяться дані за хімічним складом м’язової тканини свиней різних порід і показники-аргументи, які беруть участь в класифікації.

Початок роботи

1. У своїй робочій папці створіть нову папку 1аb9. Всі файли, які буде створено при виконанні даної роботи, зберігайте у цій папці.

2. Запустіть програму Статистика і у модулі Data Management/MFM створіть новий файл електронної таблиці для введення даних з таблиці. Збережіть цей файл під назвою Iab9.sta у свою робочу папку lab 9.

Зауваження. У першу змінну VAR1 будемо вводити гігроскопічну вологу (VOLOGA), у другу - кількість попелу (POPIL); у третю - кількість протеїну (PROTEIN), у четверту - кількість клітковини (KLITKOV), у п’яту - кількість жиру (ZHIR), у шосту - кількість - безазотистих екстрактивних речовин (BER).

3. У стовпчик NUMERIC VALUES (номера рядків) введіть назви порід свиней.

4. Виконайте команди: Статистика → Многомерные исследовательские методы → Анализ кластера.

На екрані з’явиться стартова панель модуля (рис.62) Clustering Method (методи кластерного аналізу): Joining (tree clustering) (ієрархічні агломеративні методи або деревовидна кластеризація), K - means clustering (метод К средніх), Two-way joining (двохвхідне об’єднання).

Рис. 62. Стартова панель модуля Clustering Method (методи кластерного аналізу)

У вікні Clustering Method оберіть параметр Joining (tree clustering) (вікно введення режимів роботи для ієрархічних агломеративних методів) процедура об’єднання - побудова дерева. Натиснути ОК.

5. У вікні, що відкрилось (рис.63), перейдіть на вкладнику Advanced натисніть кнопку Variables (дозволяє вибирати змінні, які беруть участь в класифікації) та виберіть всі змінні для аналізу (Select All). OK.

Рис.63. Вікно кластерний аналіз: ієрархічна класифікація

Рис. 63. Cluster Analysis: Joing (Tree Clustering)

(вікно введення режимів роботи для ієрархічних агломеративних методів)

У полі Input fill (тип вхідної інформації) залиште значення Raw data.

У полі Cluster (режим класифікації за ознаками або об’єктами)) встановіть значення Cases (raws), оскільки у вихідній таблиці породи свиней розташовані саме по рядках. ОК.

Можна вказати Amalgamation (linkage) rule (правило об’єднання) і Distance measure (метрика відстаней). Codes for grouping variable (коди для груп змінної) будуть вказувати кількість аналізованих груп об’єктів. Missing data (пропущені змінні) дозволяє вибрати або построкове видалення змінних із списку, або замінити їх на середнє значення. Open Data –дозволяє відкрити файл з даними. Причому можна вказати вимоги вибору спостережень із бази даних -кн. Select Cases. Можна задавати вагу змінним, вибравши їх із списку -кн. W.

6. У вікні Joining Results клацніть кнопку Vertical icicle plot (вертикальне дерево кластеризації). Таке подання результатів звичайно є більш наочним.

Після задання всіх необхідних параметрів і натискання кнопки ОК будуть виконані обчислення, а на екрані з’явиться вікно, яке включає в себе результати кластерного аналізу "Joining Results" рис.64.

Рис.64. Вікно, яке включає в себе результати кластерного аналізу"Joining Results"підсумок результатів та їх аналіз

Інформаційна частина діалогового вікна Joining Results Discriminant Function Analisis Results (результати аналізу кластерних функцій) повідомляє, що

Number of variables-кількість змінних;
Number of cases – кількість спостережень;
Missing data were casewise deleted – здійснена класифікація спостережень або змінних (залежить від рівня параметру в рядку Cluster в попередньому вікні налаштування.);
Amalgation (joing) rule - правило об’єднання кластерів (назва ієрархічного агломеративного методу, заданого в рядку Amalgation rules, а в попередньому вікні налаштування);
Distanse.metric is - Метрика відстані (залежить від установки в рядку Distance measure в попередньому вікні налаштування.

Одержаний графік (рис.65), на якому породи розташовані вздовж вісі абсцис (якщо ви не вводили назви порід у базі даних, то вони позначені символами С1 - С6).

Рис.65. Vertical icicle plot (Вертикальная дендрограмма)

Чим нижче пролягають лінії, що пов’язують окремі породи, тим вони більш схожі за комплексом ознак.

Графік показує, що за комплексом ознак найбільш ізольованим є свині великої чорної породи, а найбільш подібними за комплексом ознак є полтавська м’ясна і ландрас. За своїми властивостями до них найближчим є велика біла. Ізольовані проміжні позиції займають миргородська та українська степова біла породи свиней.

Збережіть цей графік у свою робочу папку lаb10.

7. Поверніться у вікно Joining Results та перейдіть на вкладинку Advanced.

8. Натисніть кнопку Distance matrix (рис. 66).

У вікні, що з’явилося, можна переглянути і вивчити відстані між всіма породами (рис.67).

Легко бачити, що змінні велика біла та українська степова біла породи дійсно знаходяться одна від одної на найменшій з усіх відстані.

Закрийте всі відкриті вікна і вимкніть програму Статистика.

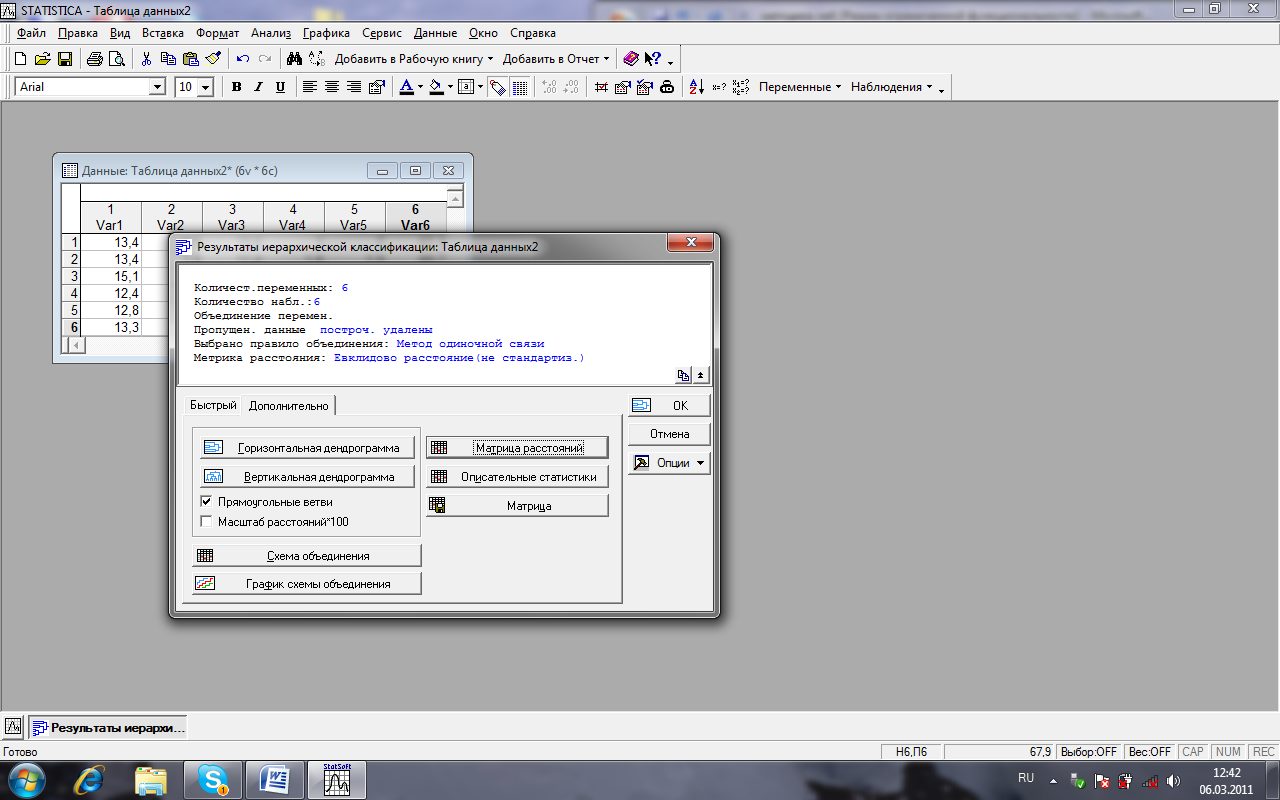
Рис.66. Вікно - результати ієрархічної класифікації

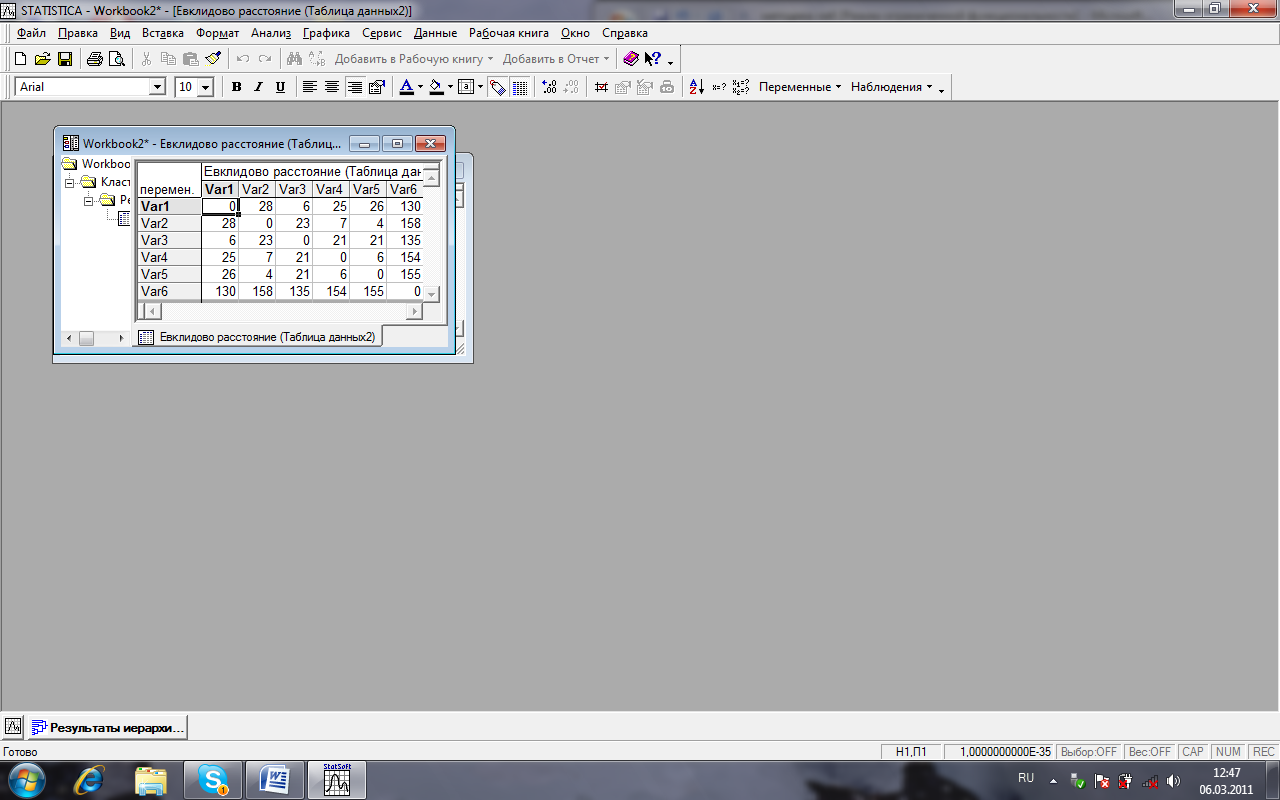
Рис.67.Вікно – Евклидова відстань

Тепер уявімо собі, що поступово (дуже малими кроками) ви «послаблюєте» ваш критерій про те, які об’єкти є унікальними, а які ні. Іншими словами ви знижуєте поріг, що відноситься до рішення про об’єднання двох або більше об’єктів в один кластер.

В результаті ви пов’язуєте разом все більше і більше число об’єктів і об’єднуєте все більше і більше число кластерів, що складаються з елементів, що більше різняться між собою. Остаточно на останньому кроці всі об’єкти об’єднуються разом. Коли дані мають зрозумілу «структуру» в термінах кластерів об’єктів, що схожі між собою, тоді ця структура, скоріше за все повинна бути відображена в ієрархічному дереві різними гілками. В результаті успішного аналізу методом об’єднання з’являється можливість виявити кластери (гілки) та інтерпретувати їх. Щоб повернутися до вікна, яке містить інші результати кластерного аналізу, необхідно натиснути на Continue та вибрати вікно Схема обьединения (рис. 68). Натисканням мишки можна розкривати рядок Amalgamation schedule, який містить протокол об’єднання кластерів (рис.69.).

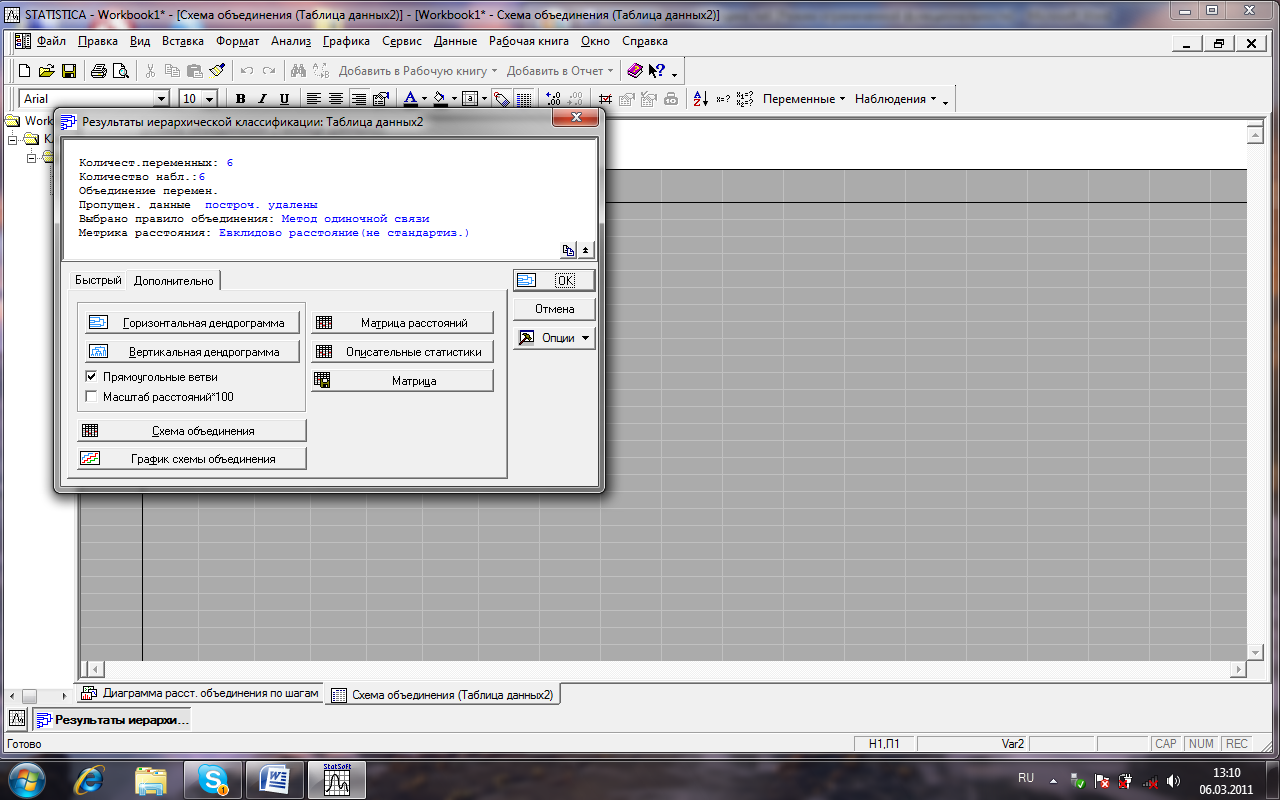
Рис.68.Вікно відбору схеми об’єднання кластерів

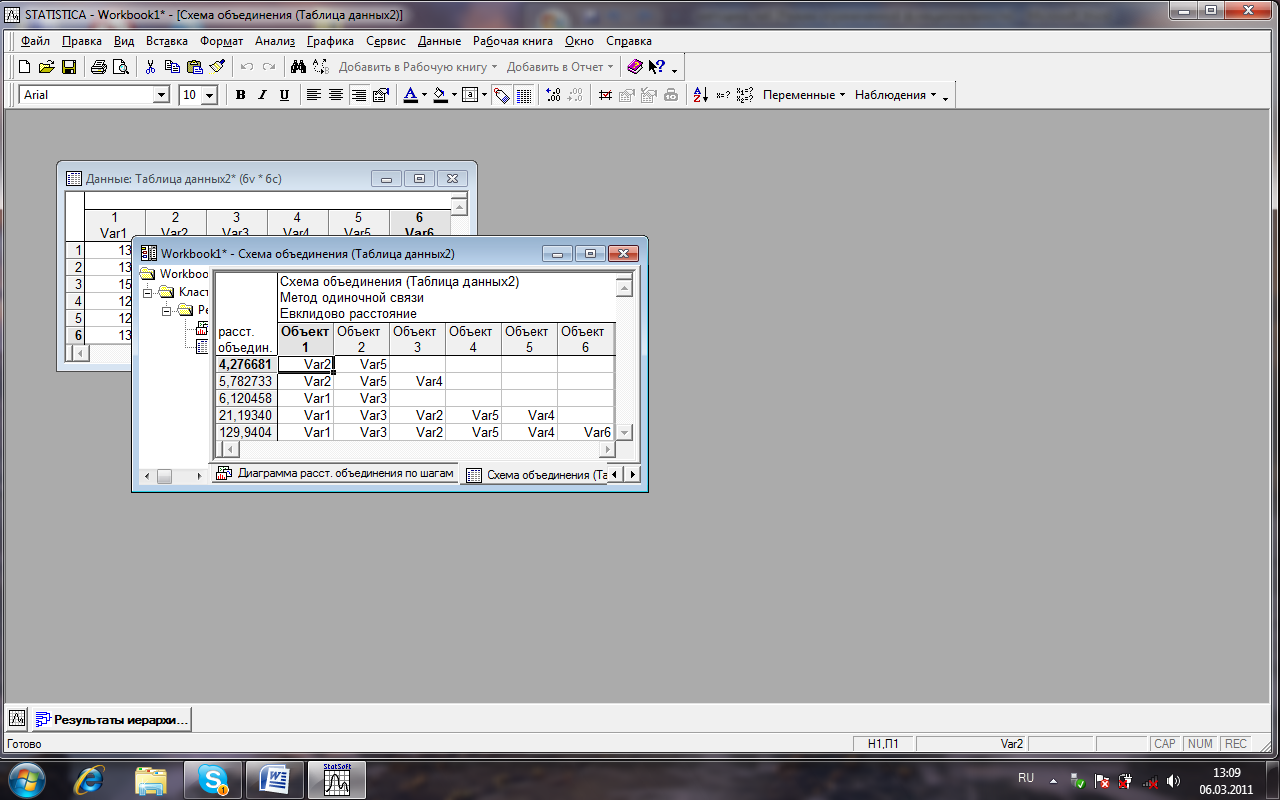
Рис.69. Amalgamation schedule (Метод одиночного зв’язку)

В заголовку вказано ієрархічний агломеративний метод і метрика відстані. Таблиця може займати декілька вікон.

Наступною у вікні результатів йде кнопка Graph of amalgamation schedule. Після натискання, відкривається вікно, яке містить ступінчате графічне зображення змінення відстані при з`єднанні кластерів рис.70.

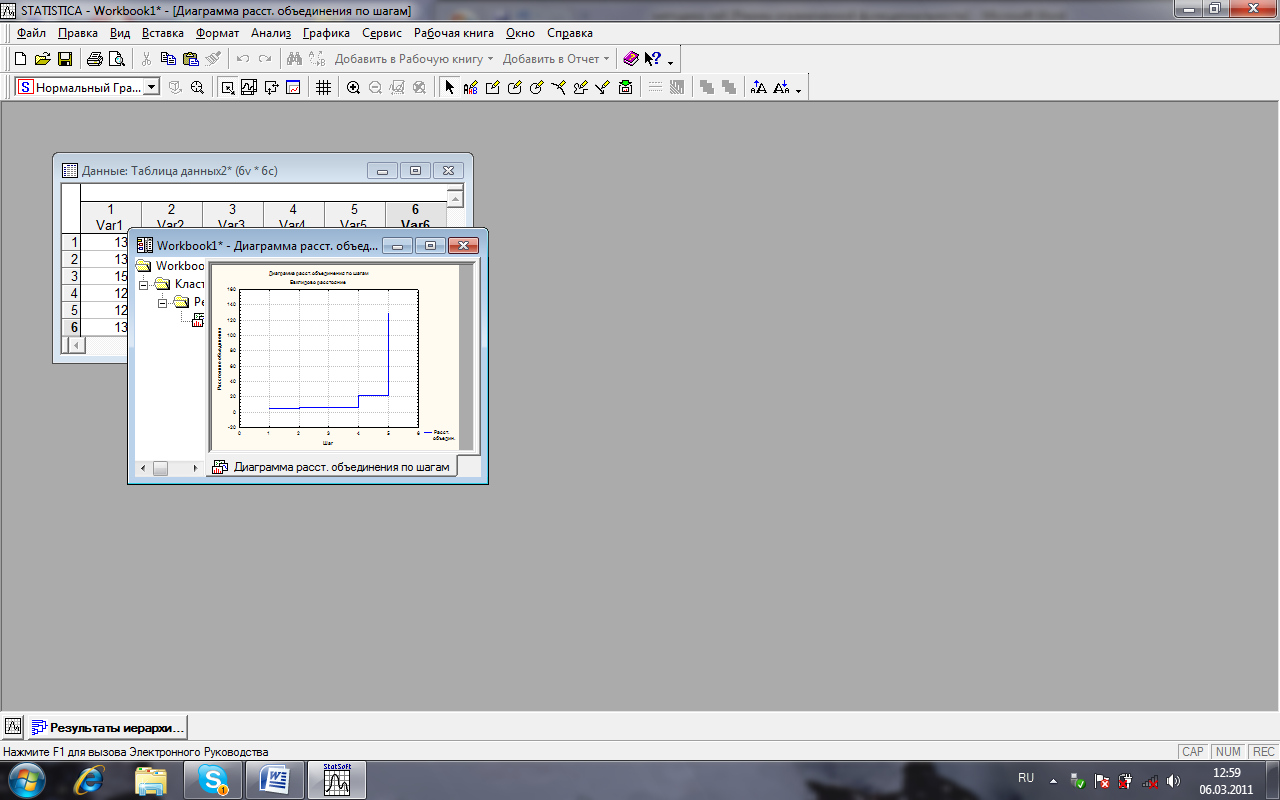
Рис.70. Вікно Graph of amalgamation schedule (Діаграма расс. обьединения по шагам)

Повернувшись в головне вікно результатів і класифікацій для перегляду матриці відстані необхідно здійснити натискання на рядку Distance matrix (рис.71).

Рис.71. Вікно матриці відстаней (Евклидова відстань)

В головному вікні результатів класифікації є рядок Save distance matrix as: (Зберегти матрицю відстані як:) дозволяюча задати ім`я файлу, в якому буде збережена матриця відстані, яка в подальшому буде підлягати обробці.

Рядок Discriptive statistics містить такі важливі описові статистики, як середнє (means) та середньоквадратичне відхилення (standart deviations) для кожного нагляду (рис.72).

Рис.72. Вікно описових статистик

При проведенні класифікації N об`єктів за k признаками, для користувача великий інтерес складають значення цих показників для кожного признаку. Для того, щоб ці характеристики розраховувались саме за признаками, необхідно повернутися в головне вікно (рис.73) вказати зміни та натиснути ОК.

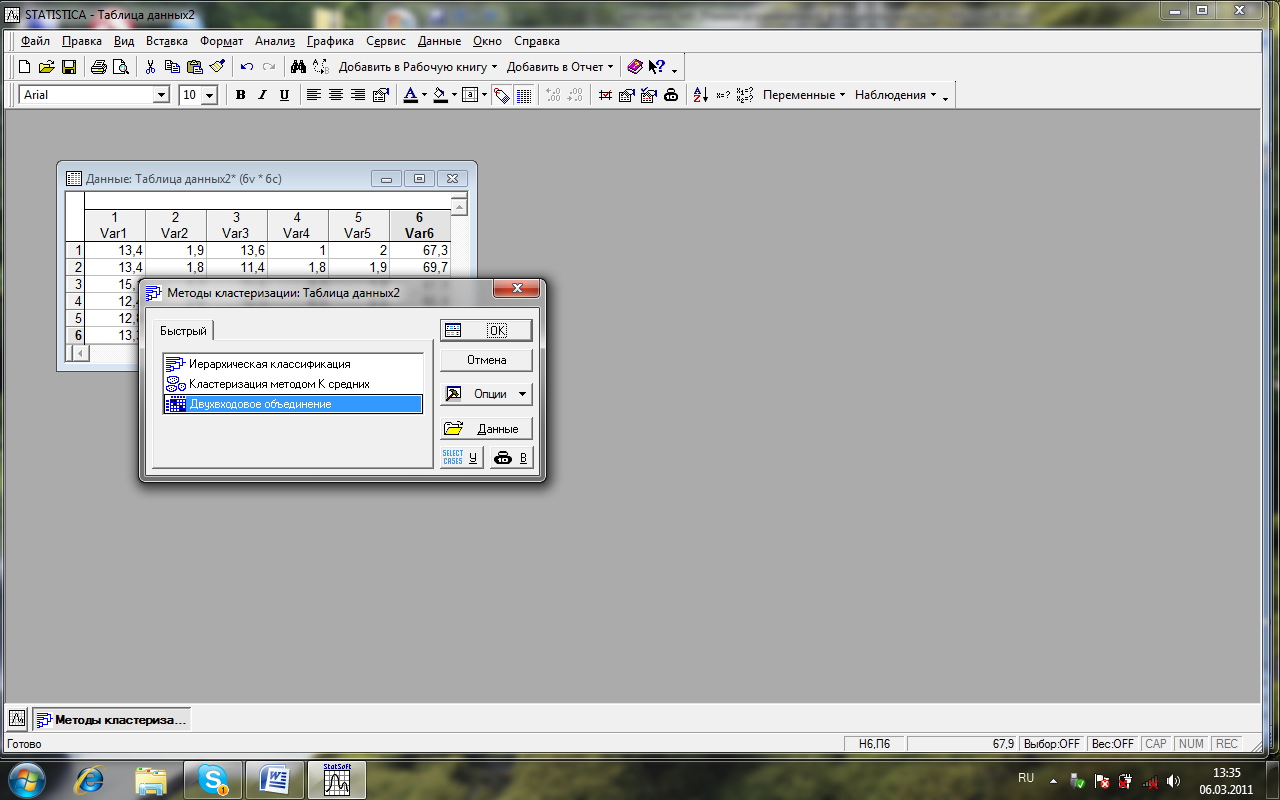
Рис. 73. Вікно двухходовое об’єднання

В вікні, яке відкривається (рис.74) вибрати функцію «Диаграмма двухходового обьединения» та натиснути ОК.

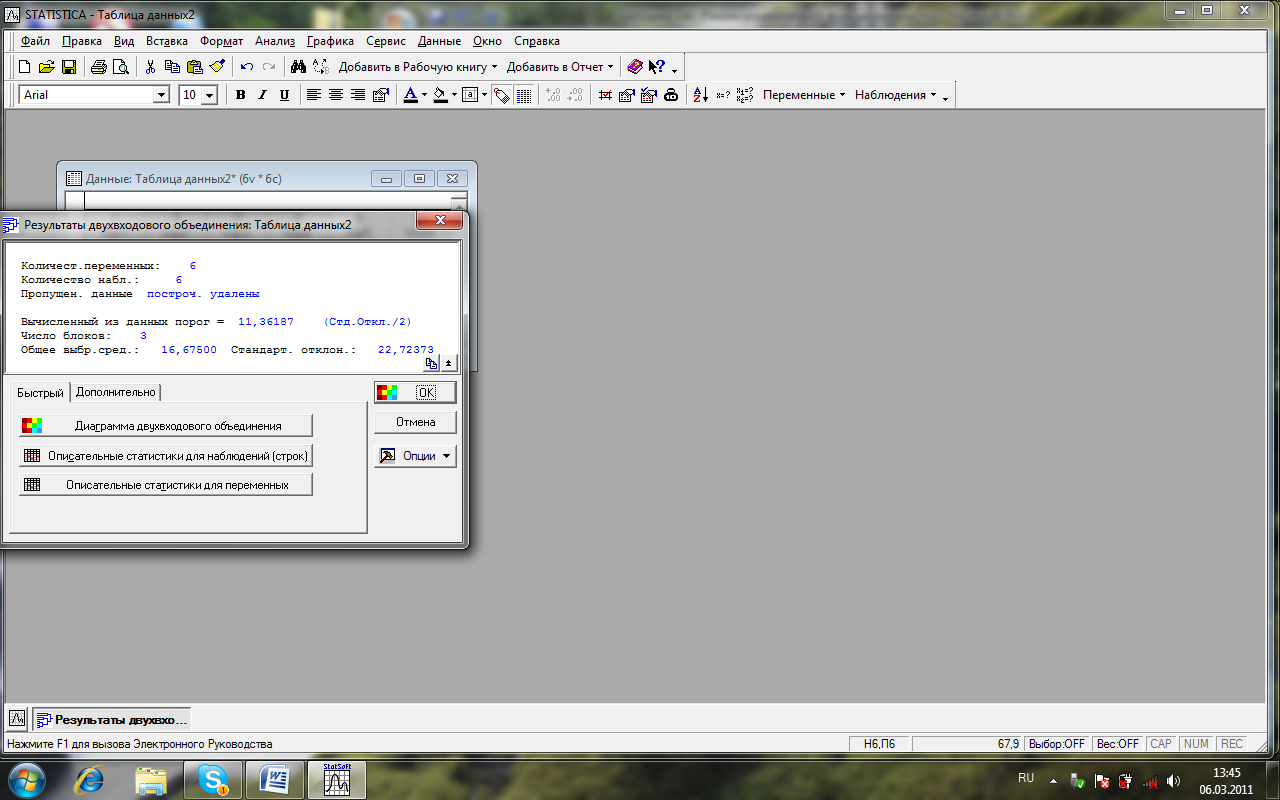
Рис.74. Вікно результати двухходового обьединения

В вікні, яке з’явиться буде представлена діаграма двухходового обьединения (рис.75).

Рис.75.Вікно результатів кластеризації методом

Two-way Joining

Питання для самоконтролю

1. Який клас задач розв’язує кластерний аналіз?

2. Вказати методи кластерного аналізу.

3. Що характеризує метрика відстаней?

4. Які статистичні параметри описової статистики містить кластерний аналіз?

5. Що відображає діаграма «двухходового об’єднання».

Пропонована література

1.Э.А. Вуколов. Основы статистического анализа. Практикум

по статистическим методам и исследованию операций с

использованием пакетов STATISTICA и EXCEL.: М.:

ФОРУМ, 2008. - 464 с.

2.А.А. Халафян. STATISTICА 6. Статистический анализ

данных.- М: ООО «Бином-Пресс», 2007. - 512 с.

3.Засуха В.А., Лисенко В.П., Голуб Б.Л. Прикладна математика: Підручник. – К.: Арістей, 2005. – 228 с.

Додаток 1

Варіанти завдань

для виконання лабораторних робіт №1 - №4

	Середньодобові надої корів по місяцях лактації, кг
№ варі анту		Надій за 305 дн. лакта ції	Місяці лактації
№ варі анту		Надій за 305 дн. лакта ції	Місяці лактації										II	111	IV	V	VI	VII	VIII	IX	X
1		2	3	4	5	6	7	8	9	10	11	12
1		2000	9,3	9,3	8,6	7,9	7,2	6,6	5,9	5.1	4,1	2,7
2		2100	9,9	9,9	9,7	8,3	7,6	6,9	6.2	5,3	4,3	2,9
3		2200	10,1	10,1	9,4	8,6	7,7	7,3	6,5	5,5	4,6	4,2
4		2300	10,5	10,5	9,8	9,0	7,8	7,5	6,8	5,9	4,3	3,4
5		2400	11,0	11,0	10,2	9.4	8,6	7,6	7,6	6.2	5,1	3,6
6		2500	11,4	11.4	10,6	9,7	9,0	8,2	7,4	6,5	5,3	3,9
7		2600	11,8	11,8	11,0	10,1	9,3	8,5	7,7	6,7	5,6	4,1
8		2700	12,2	12,2	11,4	10,5	9,6	8,9	8,0	7,0	5,9	4,3
9		2800	12,7	12,7	11,8	10,8	10,0	9,2	8.3	7,3	6,1	4,6
10		2900	13,1	13,1	12.2	11,2	10,3	9,5	8,6	7,6	6.4	4,8
11		3000	13,5	13,5	12,5	11,6	10,9	9,8	8,9	7,8	6,6	5,1
12		3100	13,9	13,9	12,9	11,9	11,0	10,1	9,2	8,1	6,9	5,3
14		3200	14,4	14,4	13,3	12,3	11,3	10,4	9,5	8,4	7,1	5,5
15		3300	14,8	14,8	13.7	12,7	11,7	10,6	9,8	8,7	7,4	5,8
16		3400	15.2	15.2	14.1	13.1	12.0	11.1	10.1	8.0	7.6	6.0
17		3500	15.6	15.6	14.5	13.4	12.3	11.4	10.4	9.0	7.9	6.2
18		3600	16.0	16.0	14.9	13.8	12.7	11.7	10.7	9.5	8.2	6.5
19		3700	16.5	16.5	15.3	14.2	13.0	12.0	11.0	9.8	8.4	6.7
20		3800	16.9	16.9	15.7	14.5	13.4	12.3	11.3	10.0	8.7	6.9
21		3900	17.3	17.3	16.1	14.9	13.7	12.7	11.5	10.3	8.9	7.2
22		4000	17.8	17.8	16.5	15.3	14.1	13.0	11.8	10.6	9.2	7.4
23		4100	18.2	18.2	16.9	15.6	14.4	13.3	12.1	10.9	9.4	7.7
24		4200	18.6	18.6	17.3	16.0	14.8	13.6	12.4	11.1	9.7	7.9
25		4300	19.0	19.0	17.7	16.4	15.1	13.9	12.7	11.4	9.9	8.1
26		4400	19.5	19.5	18.1	16.7	15.4	14.2	13.0	11.7	10.2	8.4

Додаток 2

Варіанти завдань для виконання

лабораторних робіт №,№5-9

(Регресійний, кореляційний, дисперсійний і кластерний аналізи)

Розглядаються слідуючи показники з 50 господарств:

Y₁ – продуктивність праці;

Y₂ – індекс зниження собівартості продукції;

Y₃ – рентабельність;

X₄ - затрати праці одиниці продукції;

X₅ – удільна вага робітників;

X₆ – товарність продукції ;

X₇– коефіцієнт змінності обладнання;

X₈ – премії на одного робітника;

X₉ – удільна вага втрат від збитку;

X₁₀ – фондовіддача;

X₁₁ – Прибуток від реалізації продукції.

Варіанти завдань

№ варі анту	Резуль тативна ознака, Yі	Факторна ознака, Хі	№ варі анту	Резуль тативна ознака, Yі	Факторна ознака, Хі
1	1	6,8,4,3	15	2	4,5,8,7
2	1	5,8,9,10	16	3	8,9,5,6
3	1	8,9,2,4	17	3	8,9,5,10
4	1	6,9,3,7	18	3	8,9,6,10,
5	1	8,6,4,3,	19	3	8,9,7,10
6	1	6,9,4,5	20	3	8,9,7,6
7	1	6,8,7,4	21	3	6,7,10,4
8	2	4,5,6,8	22	1	4,5,7,11
9	2	4,5,6,7	23	1	6,8,9,11
10	2	4,5,6,8	24	1	4,5,7,11
11	2	4,5,8,10	25	2	3,4,9,11
12	2	4,5,7,10	26	2	6,8,9,11
13	2	4,5,6,10	27	3	4,5,8,11
14	2	4,5,8,9	28	3	6,9,3,11

Таблиця вхідних даних

№	Y₁	Y₂	Y₃	X₄	X₅	X₆	X₇	X₈	X₉	X₁₀	X₁₁
1	9,26	204,2	13,26	0,23	0,78	70	1,37	1,23	0,23	1,45	120
2	9,38	209,6	10,16	0,24	0,75	76	1,49	1,04	0,39	1,30	115
3	12,11	222,6	13,72	0,19	0,68	80	1,44	1,80	0.43	1,37	100
4	10,81	236,7	12,85	0,17	0,70	85	1,42	0,43	0.18	1,65	105
5	9,35	62,0	10,63	0,23	0,62	87	1,35	0,88	0,15	1,91	99
6	9,87	53,1	9,12	0,43	0,76	90	1,39	0,57	0,34	1,68	95
7	8,17	172,1	25,83	0,31	0,73	94	1,16	1,72	0,38	1,94	110
8	9,12	56,5	23,39	0,26	0,71	88	1,27	1,70	0,09	1,90	105
9	5,88	52,6	14,69	0,49	0,69	75	1,16	0,84	0,14	1,94	85
10	6,30	46,6	10,05	0,36	0,73	70	1,25	0,60	0,21	2,06	92
11	6,22	53,2	13,99	0,37	0,68	65	1,13	0,82	0,42	1,96	90
12	5,49	30,1	9,68	0,43	0,74	50	1,10	0,84	0,05	1,02	85
13	6,50	146,4	10,03	0,35	0,66	55	1,15	0,67	0,29	1,85	92
14	6.61	18,1	9,13	0,39	0,72	68	1,23	1,04	0,48	0,88	95
15	4.32	13,6	5,37	0,47	0,68	72	1,39	0,66	0,41	0,62	85
16	7,37	89,9	9,86	0,30	0,77	95	1,38	0,86	0,62	1,09	95
17	7,02	62,5	12,62	0,32	0,78	85	1,35	0,79	0,56	1,69	94
18	8,25	46,3	5,02	0,25	0,78	78	1,42	0,34	1,76	1,53	102
19	8,15	103,5	21,18	0,31	0,81	68	1,37	1,60	1,31	1,40	100
20	8,72	73,3	25.17	0,26	0,79	85	1,41	1,46	0,45	2,22	109
21	6,64	76,6	19,40	0,37	0,77	80	1,35	1,27	0,50	1,32	96
22	8,10	73,01	21,00	0,29	0,78	75	1,48	1,58	0,77	1.48	102
23	5,52	32,3	6,57	0,34	0,72	70	1,24	0.68	0172	0,69	88
24	9,37	199,6	14,19	0,23	0,79	87	1,40	0,86	1,29	2,39	125
25	13.17	598,1	15,81	0,17	0,77	91	1,45	1,98	0,21	1,37	135
26	6.67	71,2	5,23	0,29	0,80	83	1,40	0,33	0,25	1,51	79
27	5,68	90.8	7,99	0,49	0,71	79	1,28	0,45	0,15	1.43	96
28	5,22	82,1	17,50	0,41	0,79	91	1,33	0,74	0,66	1,82	92
29	10,02	76,2	17,16	0,41	0,76	78	1,22	0,03	0,74	2,52	132
30	8.16	119,5	14,54	0,29	0,78	87	1,28	0.99	0,99	1,75	124

Додаток 3

Критичні точки t - критерія Ст´юдента при різних степенях значимості α та вільності m [3]

m	α=0,05	α =0,01	α =0,001	m	α =0,05	α =0,01	α =0,001
1	12.7060	63.656	64.60	28	2.0484	2.7633	3.6739
2	4.3020	9.924	31.599	29	2.0452	2.7564	3.8494
3	3.182	5.840	12.924	30	2.0423	2.7500	3.6460
4	2.776	4.604	8.610	32	2.0360	2.7380	3.6210
5	2.570	4.0321	6.863	34	2.0322	2.7284	3.6007
6	2.4460	3.7070	5.958	36	2.0281	2.7195	3.5821
7	2.3646	3.4995	5.4079	38	2.0244	2.7116	3.5657
8	2.3060	3.3554	5.0413	40	2.0211	2.7045	3.5510
9	2.2622	3.2498	4.780	42	2.018	2.6980	3.5370
10	2.2281	3.1693	4.5869	44	2.0154	2.6923	3.5258
11	2.201	3.105	4.437	46	2.0129	2.6870	3.5150
12	2.1788	3.0845	4.178	48	2.0106	2.6822	3.5051
13	2.1604	3.1123	4.220	50	2.0086	2.6778	3.4060
14	2.1448	2.976	4.140	55	2.0040	2.6680	3.4760
15	2.1314	2.9467	4.072	60	2.0003	2.6603	3.4602
16	2.1190	2.9200	4.0150	65	1.997	2.6536	3.4466
17	2.1098	2.8982	3.965	70	1.9944	2.6479	3.4350
18	2.1009	2.8784	3.9216	80	1.9900	2.6380	3.4160
19	2.0930	2.8609	3.8834	90	1.9867	2.6316	3.4019
20	2.08600	2.8453	3.8495	100	1.9840	2.6259	3.3905
21	2.2.0790	2.8310	3.8190	120	1.9719	2.6174	3.3735
22	2.0739	2.8188	3.7921	150	1.9759	2.6090	3.3566
23	2.0687	2.8073	3.7676	200	1.9719	2.6006	3.3398
24	2.0639	2.7969	3.7454	250	1.9695	2.5966	3.3299
25	2.0595	2.7874	3.7251	300	1.9679	2.5923	3.3233
26	2.059	2.778	3.7060	400	1.9659	2.5882	3.3150
27	2.0518	2.7707	3.6896	500	1.9640	2.7850	3.310

Додаток 4

Критичні точки F критерію Фішера (F = σ²₁ / σ²₂)при значимості α =5% (верхній рядок) та α =1%(нижній рядок)та степенях вільності m₁ і m₂ вибірок [3]

m₂	m₁
m₂	1	2	3	4	5	6		7	8	9	10
1	161	200	216	225	230	234		237	239	241	242
1	4052	4999	5403	5625	5764	5889		5928	5981	6022	6054
2	18,5	19,0	19,2	19,25	19,3	19,33		19,36	19,37	19,38	19,38
2	98,5	99,0	99,2	99,25	99,3	99,33		99,34	99,36	99,38	99,4
3	10,1	9,6	9,3	9,1	9,0	8,94		8,88	8,84	8,81	8,78
3	34,1	30,8	29,5	28,7	28,2	27,9		27,7	27,5	27,3	27,2
4	7,7	7,0	6,6	6,4	6,3	6,2		6,1	6,04	6,0	5,96
4	21,2	18,0	16,7	16,0	15,5	15,2		15,0	14,8	14,7	14,5
5	6,6	5,8	5,4	5,2	5,1	5,0		4,9	4,8	4,78	4,74
5	16,3	13,3	12,1	11,4	11,0		10,7	10,5	10,3	10,2	10,1
6	6,0	5,1	4,8	4,5	4,4		4,3	4,2	4,15	4,1	4,06
6	13,8	11,0	9,8	9,2	8,8		8,5	8,3	8,1	8,0	7,9
7	5,6	4,7	4,4	4,1	4,0		3,9	3,8	3,7	3,68	3,63
7	12,3	9,6	8,5	7,9	7,5		7,2	7,0	6,8	6,7	6,6
8	5,3	4,5	4,1	3,8	3,7		3,6	3,5	3,44	3,4	3,34
8	11,3	8,7	7,6	7,0	6,6		6,4	6,2	6,0	5,9	5,8
9	5,1	4,3	3,9	3,6	3,5		3,4	3,3	3,2	3,18	3,13
9	10,6	8,0	7,0	6,4	6,1		5,8	5,6	5,5	5,4	5,3
10	5,0	4,1	3,7	3,5	3,3		3,2	3,1	3,07	3,02	2,97
10	10,0	7,6	6,6	6,0	5,6		5,4	5,2	5,1	5,0	4,9
11	4,8	4,0	3,6	3,4	3,2		3,1	3,0	2,95	2,9	2,86
11	9,9	7,2	6,2	5,7	5,3		5,1	4,9	4,7	4,6	4,5
12	4,75	3,9	3,5	3,3	3,1		3,0	2,9	2,85	2,8	2,76
12	9,3	6,9	6,0	5,4	5,1		4,8	4,7	4,5	4,4	4,3