Файл: Проектирование и исследование механизма.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 08.11.2023

Просмотров: 249

Скачиваний: 4

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Запишем векторное уравнение для скорости точки В: 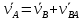(2.5)В этом уравнении нам известны направления векторов скоростей 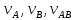. Скорость точки В направлена по направляющей t-t, скорость точки А направлена перпендикулярно кривошипу ОА, а скорость звена АВ направлена перпендикулярно этому звену. Зная направления скоростей и значение скорости точки А, решим уравнение (2.5) графически. Для этого определим значение масштабного коэффициента, который необходим для построений. Он определяется аналогично масштабному коэффициенту, найденному в п. 2.1.1: 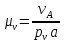(2.6)где 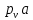– длина вектора, изображающего на плане скоростей вектор скорости 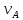(в данном случае 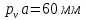) 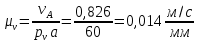(2.7)После определения масштабного коэффициента решаем векторное уравнение (2.1). Для этого отметим точку – полюс, из него проводим отрезок 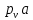, равный значению скорости точки А и направленный перпендикулярно кривошипу ОА. Из конца построенного отрезка проводим линию действия относительной скорости, который направлен перпендикулярно АВ, в точке пересечения этого вектора с направляющей t-t, будет находиться точка b. 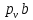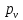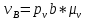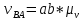Вектор определяет скорость точки В, он направлен из полюса .Численное значение скоростей определим, измерив, полученные отрезки и перемножив их на масштабный коэффициент: (2.8) (2.9)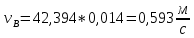 (2.10) 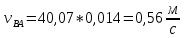(2.11)Угловую скорость рассчитаем по формуле:
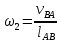
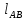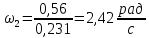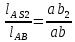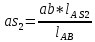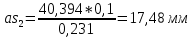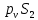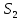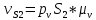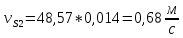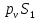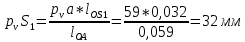
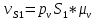
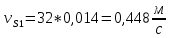
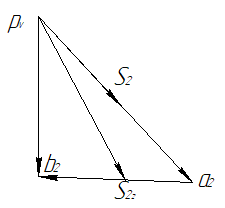
(2.12)где – длина шатуна (м). (2.13)Положение центров масс на плане скоростей будут определяться по принципу подобия: (2.14) (2.15) (2.16)Из полюса в центр масс проводим вектор , который будет указывать направление скорости центра масс шатуна . Эта скорость будет равна: (2.17) (2.18)По аналогичной пропорции находим вектор .Полный план скоростей для второго положения показан на рис. 2.3:Рис. 2.3 План скоростей для 2-го положения механизмДля остальных положений все вычисления и построения делаем аналогичным способом. Все вычисления приведены в таблице 2.Таблица 2

Скорость
Положения механизма

1
2
3
4
5
6
7
8
9
10
11
12



м/с
0,826
0,826
0,826
0,826
0,826
0,826
0,826
0,826
0,826
0,826
0,826
0,826



м/с
0,31
0,593
0,79
0,80
0,56
0
0,43
0,81
0,88
0,67
0,34
0



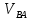м/с
0,79
0,56
0,18
0,24
0,60
0
0,81
0,59
0,20
0,26
0,64
0



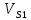м/с
0,448
0,448
0,448
0,448
0,448
0,448
0,448
0,448
0,448
0,448
0,448
0,448



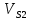м/с
0,52
0,68
0,805
0,809
0,65
0
0,55
0,76
0,84
0,75
0,57
0





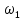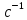14
14
14
14
14
14
14
14
14
14
14
14





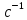3,41
2,42
0,77
1,03
2,59
0
3,5
2,5
0,86
1,12
2,77
0
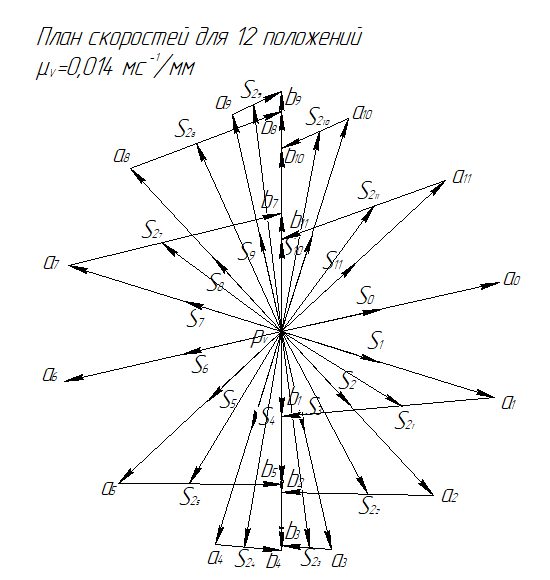
Рис. 2.4 План скоростей для 12-ти положений механизма.
2.1.4 Расчёт ускорений для рабочего и холостого положения.Расчёт ускорений проводится для двух положений рабочего хода механизма, либо для одного на рабочем и одного на холостом ходу, в которых сила полезного сопротивления не равна нулю. В данном случае будет проводиться расчёт для 2-го положения.Первоначально определим ускорение точки А кривошипа. Оно является постоянным и равно произведению квадрата угловой скорости кривошипа на его длину: 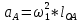(2.19) 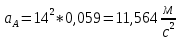(2.20)Нахождение ускорений будем производить методом планов, для этого запишем векторное уравнение ускорения точки В: 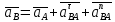(2.21)где 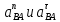– вектора нормальной и тангенциальной составляющей ускорения звена АВ соответственно.Решим уравнение (2.21) графически. Для этого примем масштабный коэффициент плана ускорений 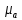, равный: 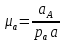(2.22)где 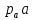=70 мм. 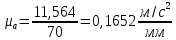(2.23)Строим план ускорений согласно направлению векторов:- 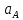направлен из точки А в точку О;- 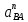направлен из точки В в точку А;- 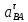направлен перпендикулярно звену АВ;- направление 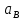задается направляющей t-t.Определим нормальную составляющую ускорения звена АВ: 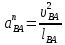(2.24) 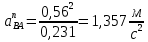(2.25)Для построения плана ускорений:

  • выбираем полюс ;

  • строим вектор ускорения точки А;

  • из конца вектора строим луч параллельный звену АВ, и на этом луче откладываем отрезок 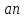равный: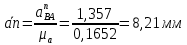

  • через точку n проводим прямую перпендикулярную АВ, отмечаем точку пересечения ее с направляющей t-t – точка ;

  • отрезок – ускорение точки В на плане ускорений.
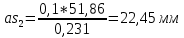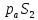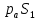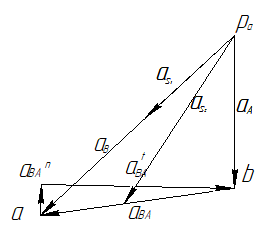
Ускорения центров масс определим, использую формулу 2.14 из п. 2.1.3 (2.26)Из полюса в центр масс проводим вектор , который будет указывать направление ускорения центра масс шатуна . По аналогичной пропорции находим вектор .На рис. 2.5 представлен план ускорений для второго положения. Рис. 2.5 План ускорений для 2-го положения.
Численные значения ускорений вычислим по формулам:
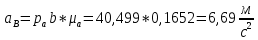
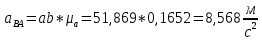
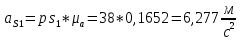
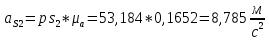
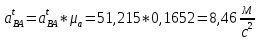
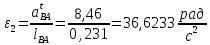
Значения для плана ускорений 11 рассчитывается аналогично. Результаты расчёта ускорений приведены в таблице 3
Таблица 3

Ускорения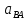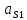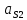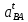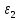































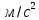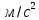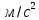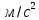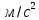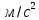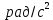2
11,564
6,69
8,568
6,277
8,785
8,46
36,6233

11
11,564
9,42
7,907
6,277
9,984
7,70
33,3333

Смотрите также файлы