Файл: Курсовая работа по дисциплине Общая химическая технология.docx
Добавлен: 08.11.2023
Просмотров: 100
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1.2 Результаты и обсуждения эксперимента
1.2.1 Фракции столбца
Как объяснялось во введении, равные количества двух образцов поли(α-метилстирола), оба из которых имели очень узкое молекулярно-массовое распределение, смешивали и фракционировали на колонке для определения молекулярно-массового распределения смеси. Полученное молекулярно-массовое распределение сравнивали с молекулярно-массовым распределением компонентов. На рисунке 1А сравнение выполнено для образца № 9, в котором молекулярные массы обоих компонентов достаточно различаются (Mω/Mn=1,27). Определенное молекулярно-массовое распределение смеси согласуется с молекулярно-массовым распределением, рассчитанным по тем компонентам, которые также определяются с помощью осаждающей хроматографии. На рисунке 1Б молекулярно-массовое распределение смеси Mω/Mn = 1,11 (№ 10) также четко показано методом элюирования. Однако если Mω/Mn составляет всего 1,04 и 1,02, их молекулярно-массовое распределение не может быть показано ни с помощью элюционной хроматографии, ни с помощью хроматографии преципитации, как показано на рисунках 1C и D. Из этих сравнений мы можем заключить, что:
а) если образец имеет молекулярно-массовое распределение более узкое, чем Mω/Mn = 1,1 в этом диапазоне молекулярных масс колоночное фракционирование не будет эффективным.
b) не наблюдается заметной разницы между разрешающей способностью преципитационной хроматографии и методом элюции в настоящих экспериментальных условиях.
Обычно считается, что прецизионная хроматография обеспечивает превосходное разрешение, обычно не подвергая сомнению эффективность температурного градиента.
На практике превосходство осадительной хроматографии над методом элюирования иногда подтверждалось экспериментально, но разница между двумя методами была меньше, чем можно было ожидать, исходя из элементарного рассмотрения работы колонок. Для выяснения причины неожиданно небольшой разницы между двумя методами был проведен анализ молекулярной массы и количества полимера, отложившегося на стеклянных шариках в процессе преципитационной хроматографии. В осаждающей хроматографии предполагается, что полимеры, растворенные в более высокотемпературной области колонки, осаждаются на стеклянных шариках при более низкой температуре. Следовательно, если подача растворителя прекращается, когда растворитель увеличивается на количество, достаточное для прохождения образца через всю колонку, и раствор выталкивается из колонки с газообразным азотом с той же скоростью, можно ожидать, что молекулы полимера останутся осажденными на стеклянных шариках в колонке. По этому методу была получена смесь № 9, и колонка была разделена на 13 частей. Определяли количество и молекулярную массу полимеров, осевших на стеклянных шариках в каждом срезе. Полученные результаты представлены в таблице 1.3. Видно, что на участке № 5 имеется прерывистая граница, выше которой все осаждающиеся полимеры имеют молекулярную массу 3 · 10
4, а ниже ее 12 · 104. Причем, несмотря на то, что около 32,5 % исходного количества образца остались на стеклянных шариках, покрытых первоначально (участок № 1), на картине седиментации показан четкий одиночный пик. Из этих результатов можно сделать вывод, что переосаждение действительно происходило за счет температурного градиента, но эффективность фракционирования на первой стадии была настолько высока, что на первой стадии осуществлялось почти полное разделение компонентов смеси.
Таблица 1.3 – Молекулярная масса и количество образца, нанесенного на стеклянные шарики в процессе преципитационной хроматографии
| № | Масса нанесенного полимера, % | [η], дл/г | Mυ · 10-4 |
| 1 | 32 | 0,87 | 32 |
| 2 | 12 | 0,88 | 32 |
| 3 | 6 | 0,85 | 31 |
| 4 | 1 | 0,63 | 20 |
| 5 | 1 | — | — |
| 6 | 4 | 0,43 | 11 |
| 7 | 12 | 0,46 | 12 |
| 8 | 9 | 0,45 | 12 |
| 9 | 6 | 0,43 | 11 |
| 10 | 7 | 0,44 | 12 |
| 11 | 4 | 0,41 | 10 |
| 12 | 2 | 0,40 | 10 |
| 13 | 3 | 0,14 | 2,3 |
| элюировать | 1 | — | — |
| Образец № 9; расход 23 мл/ч; общее количество пробы 655,8 мг; выход 107 % (небольшое количество клея от чувствительной к давлению ленты могло быть растворено в растворе образца, когда колонка была разрезана на 13 частей). | |||
1.2.2 Гель-проникающая хроматография
На рисунке 1.2 кажущееся молекулярно-массовое распределение смеси (№ 9), рассчитанное по ГПХ, сравнивается с распределением ее компонентов. Хотя между пиками компонента с более высокой молекулярной массой наблюдается небольшая вариация, совпадение вполне удовлетворительное. Однако разрешение ГПХ недостаточно велико, чтобы можно было различить два пика на хроматограмме образца № 11.
1.2.3 Метод скорости осаждения
Этот метод, по-видимому, имеет самое высокое разрешение из всех используемых здесь методов, поскольку он смог показать двойные пики в картине седиментации образца № 11, которые нельзя было показать никаким другим методом. Интегральная функция распределения кажущегося коэффициента седиментации G*(Sc*, t, C0) получается из формулы
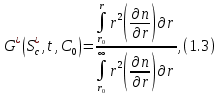
в зависимости от времени t. Здесь n — показатель преломления раствора в точке r и времени t, r0 — радиальное расстояние от центра вращения до мениска воздух-жидкость. Из кривых зависимости G* от r, полученных таким образом для различных t, мы находим Sc* для заданного G* как функцию от t, используя следующее уравнение:
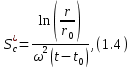
где ω— угловая скорость ротора, t — наблюдаемое время, t0 — нулевая временная поправка. Коррекция нулевого времени t0 может быть определена путем экстраполяции графика зависимости (rh2 – r02) от t к rh = r0, где rh является положением пика.
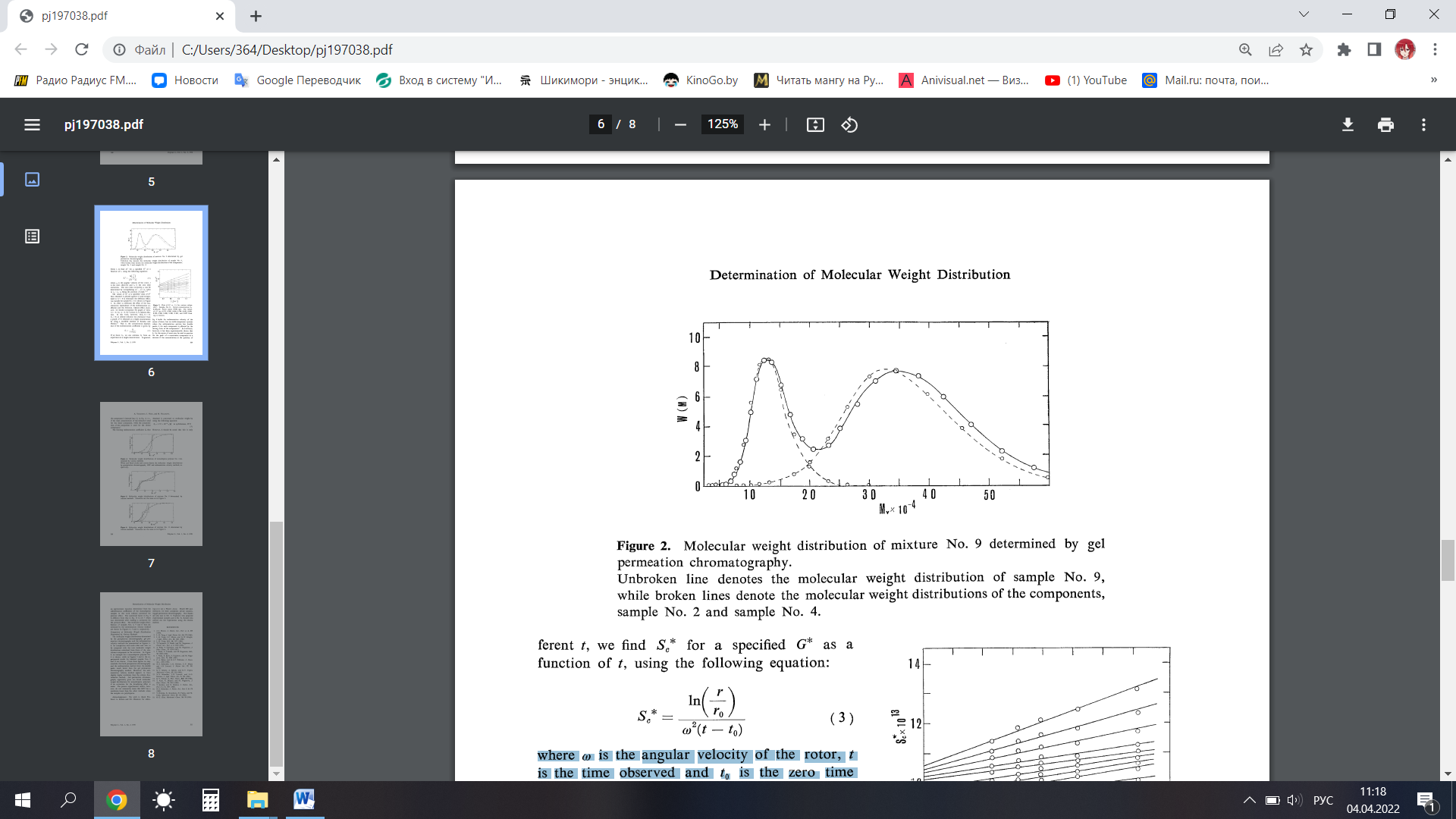
Рисунок 1.2 – Молекулярно-массовое распределение смеси № 9, определенное методом гель-проникающей хроматографии
Сплошная линия обозначает молекулярно-массовое распределение образца № 9, а пунктирные линии обозначают молекулярно-массовое распределение компонентов, образца № 2 и образца № 4.
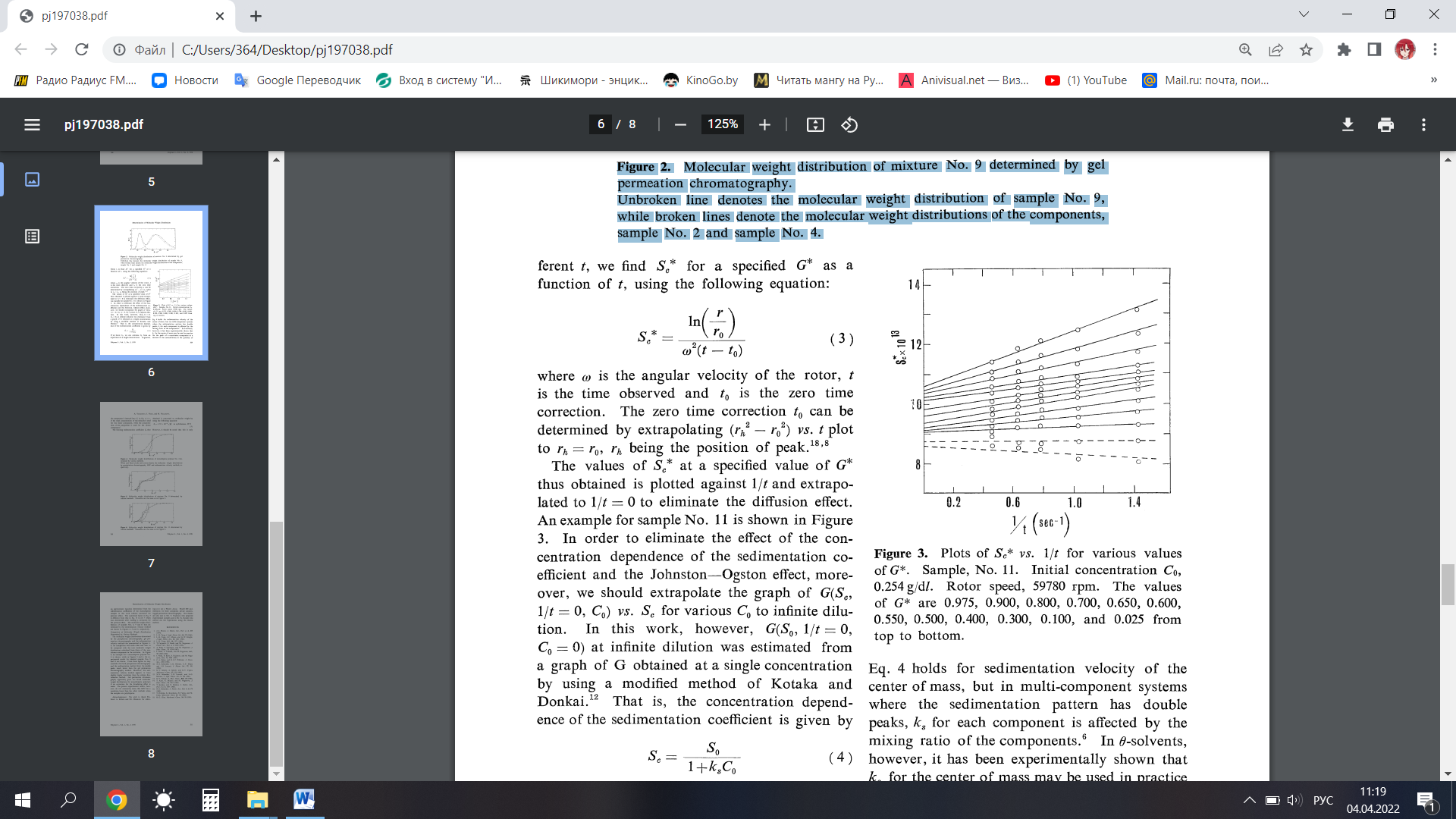
Рисунок 1.3 – Графики зависимости Sc* от 1/t для различных значений G*. Образец № 11. Исходная концентрация Co 0,254 г/сут. Частота вращения ротора, 59780 об/мин. Значения G* составляют 0,975, 0,900, 0,800, 0,700, 0,650, 0,600, 0,550, 0,500, 0,400, 0,300, 0,100 и 0,025 сверху вниз.
Полученные таким образом значения Sc* при заданном значении G* наносят на график относительно 1/t и экстраполируют до 1/t = 0, чтобы исключить эффект диффузии. Пример для образца № 11 показан на рисунке 1.3. Для исключения влияния концентрационной зависимости коэффициента седиментации и эффекта Джонстона-Огстона, кроме того, следует экстраполировать график G(Sc, l/t = 0, C0) по сравнению с Sc для различных C0 до бесконечного разбавления. Однако в этой работе G(S0, 1/t = 0, C0 = 0) при бесконечном разбавлении оценивали по графику G, полученному при одной концентрации с использованием модифицированного метода Котаки и Донкаи. То есть концентрационная зависимость
коэффициента седиментации имеет вид
Зная ks, мы можем оценить S0 из эксперимента при одной концентрации. В общем, уравнение 1.5 справедливо для скорости седиментации центра масс, но в многокомпонентных системах, где характер седиментации имеет двойные пики, ks для каждого компонента зависит от соотношения компонентов в смеси. Однако в ɵ-растворителях было экспериментально показано, что ks для центра масс может быть использовано для пика составляющего компонента в смеси, если концентрация в положении компонента подставлена в C0 в уравнение 1.5, т.е. если для более быстрого компонента используется общая концентрация смеси, а для более медленного компонента используется концентрация компонента.
Полученный таким образом предельный коэффициент седиментации S0 пересчитывается в молекулярную массу по следующей формуле:
в циклогексане, 35°С.
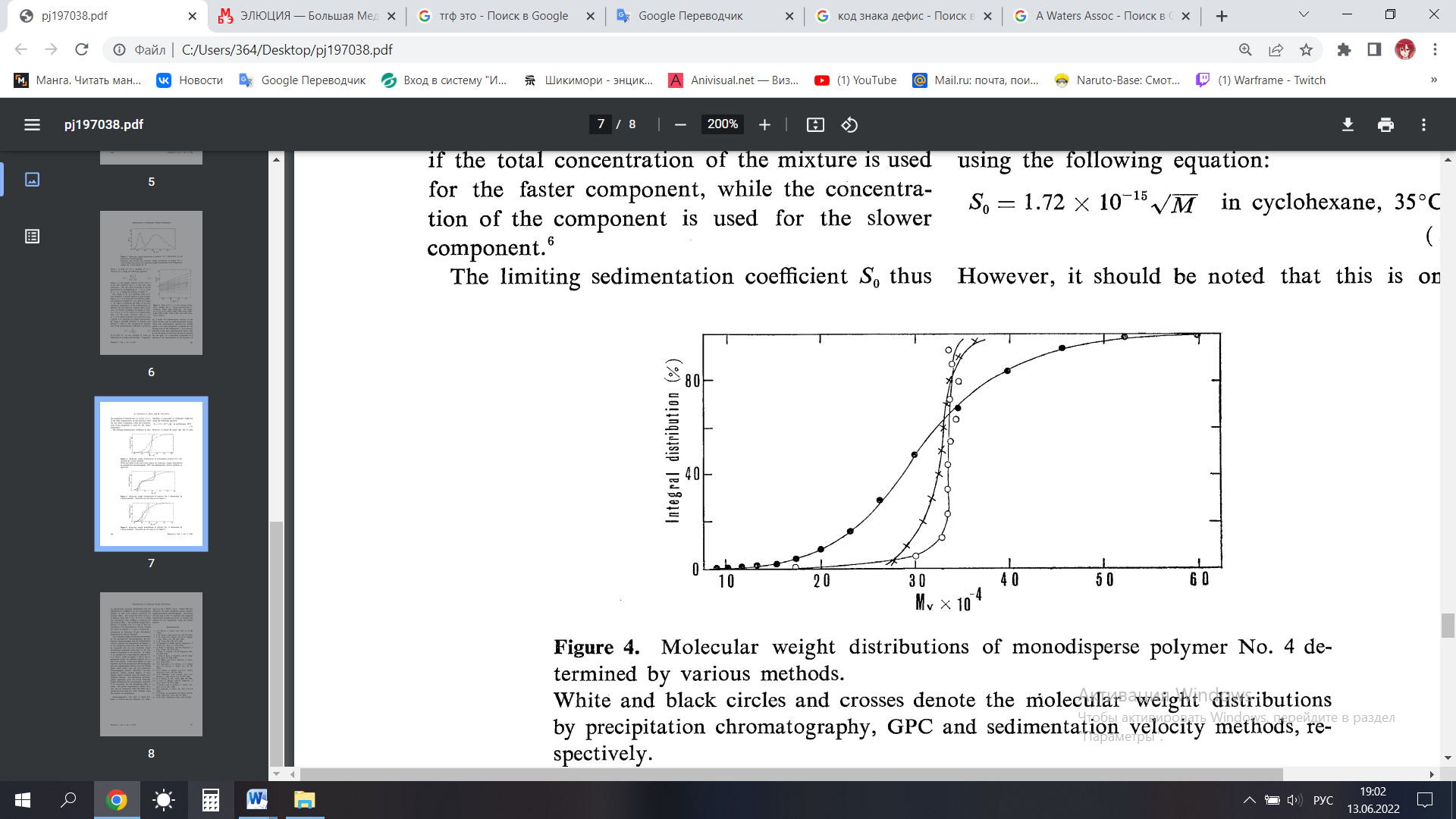
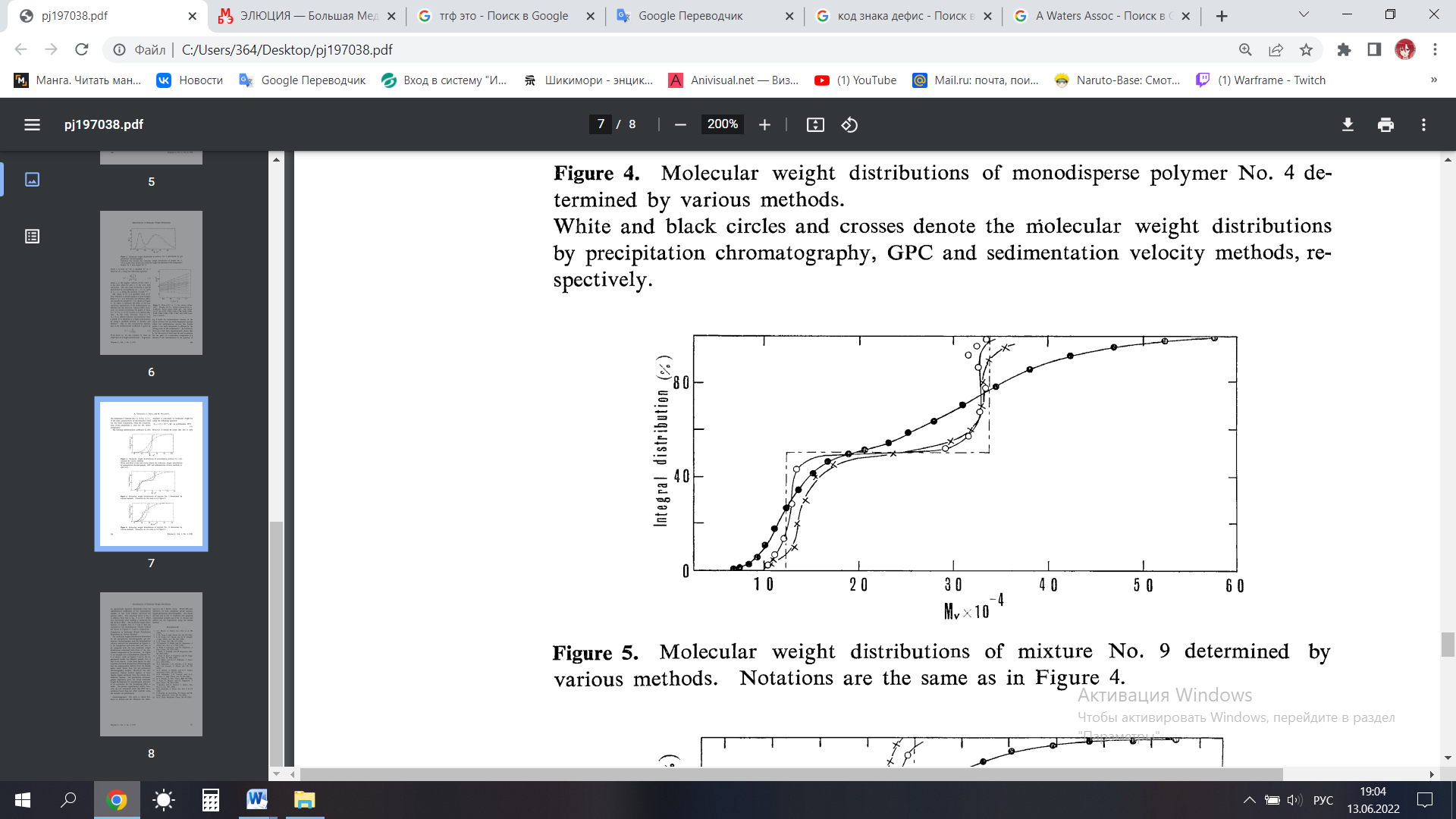
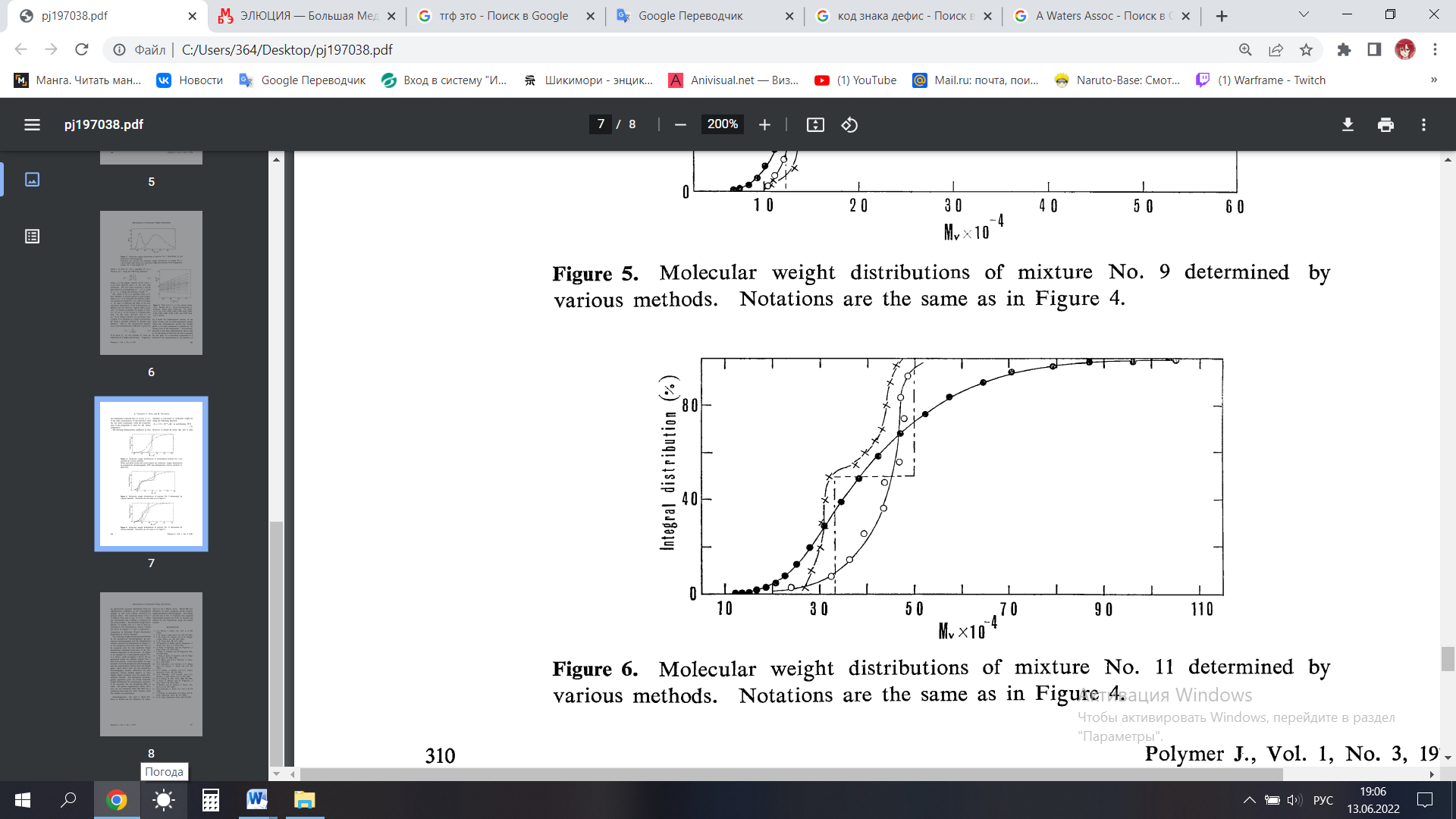
Однако следует отметить, что это лишь приближенное уравнение, полученное из коэффициентов седиментации монодисперсных образцов в данной работе без поправки на влияние давления. Молекулярно-массовые распределения образцов № 4, 9 и 11, определенные методом скорости седиментации, показаны на рисунках 1.4, 1.5 и 1.6 соответственно.

Интегральное распределение (%)
Рисунок 1.4 – Молекулярно-массовые распределения монодисперсного полимера № 4, определенные различными методами
Белые и черные кружки и кресты обозначают молекулярно-массовое распределение, полученное методами преципитационной хроматографии, ГПХ и скорости седиментации, соответственно.

Интегральное распределение (%)
Рисунок 1.5 – Молекулярно-массовые распределения смеси № 9, определенные различными методами (обозначения те же, что и на рисунке 1.4)

Интегральное распределение (%)
Рисунок 1.6 – Молекулярно-массовые распределения смеси № 11, определенные различными методами (обозначения те же, что и на рисунке 1.4)
1.3 Определение молекулярно-массового распределения полимеров по данным аналитического суммарного фракционирования или турбидиметрического титрования
Определение молекулярно-массового распределения (ММР) по данным аналитического суммативного фракционирования или турбидиметрического титрования растворов полимеров относится к типичным обратным задачам физики полимеров. В настоящее время известны как аналитические, так и аппроксимативные методы решения этой задачи. Аналитические методы связанные с решением интегральных уравнений Фредгольма первого рода, относятся к нечетким математическим задачам и требуют применения специальных мер регуляризации. Кроме того, формулировка исходных интегральных уравнений представляет собой далеко не тривиальную задачу. Классические аппроксимативные методы Мори-Тэмблина и Классона страдают рядом принципиальных недостатков. Возможности метода, предложенного в, исследованы как экспериментально, так и теоретически; на ряде модельных примеров показано, что метод Рейнера позволяет определять характеристики ММР с приемлемой точностью [6].
Здесь представлен новый метод решения обратной задачи дробления. Предлагаемая процедура более точна, чем метод Рейнера; соответствующий математический аппарат значительно проще, чем требуется при решении интегральных уравнений, и не намного сложнее, чем в методе Рейнера. Предлагаемый алгоритм устойчив по отношению к экспериментальной и не требует какой-либо регуляризации. Теоретическая основа нового метода включает уравнение материального баланса при фазовом разделении растворов полимеров [7].
Рассмотрим функцию
где f(M) — нормализованная дифференциальная ММР, а M — молекулярная масса. Функция I (M) представляет собой дополнение к обычному кумулятивному ММР, F (M) = 1 - I (M), и соответствующее условие нормировки, I (0) = 1. Пусть c (γ, M) — растворимость монодисперсного полимера; γ - параметр фракционирования, который может представлять параметр взаимодействия Флори-Хаггинса χ, объемную долю осадителя, температуру и т. д.