Предлагается определять функцию I (М) по данным фракционирования или турбидиметрического титрования с помощью двух уравнений:





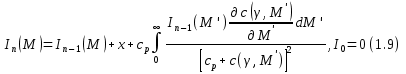
где с_p = x, с_о — концентрация, а х — доля осажденного полимера, Со — концентрация полимера в пересчете на объем системы (равна исходной концентрации полимера в системе). Уравнение 1.8 согласуется с аналогичным соотношением в методе Рейнера и служит для определения М, которое соответствует заданному значению. Итерационное уравнение 1.9 позволяет вычислить I (М) при значении М, определяемом из формулы 1.8. Можно показать, что итерационный процесс, определяемый в 1.9, сходится к I(M) с точностью, зависящей от точности уравнения материального баланса.

Модельные расчеты показали, что сходимость итерационного процесса, определяемого формулой 1.9, достаточно быстрая, так что уже вторая итерация дает более точные результаты, чем метод Рейнера. В результате второе уравнение в предлагаемом методе можно записать в виде


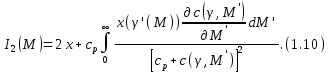
Во избежание недоразумений отметим, что значение x в интеграле 1.10 берется в точке γ', которая, в свою очередь, соответствует M', заданному уравнением 1.8.

Быстрая сходимость уравнения 1.9 и достаточная точность уравнения 1.10 обусловлены тем, что первая итерация совпадает с уравнением, используемым в методе Рейнера, возможности которого подробно исследованы:


Предлагаемый метод (по аналогии с процедурой Райнера) приводит непосредственно к функции I(М), и мы имеем f (M) = - dl/dM. Однако можно вывести уравнение для f(M), аналогичное (1.9):







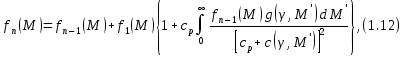
Функция f₁(M) есть дифференциальная ММР, полученная на первой итерации.

Заметим, что уравнения 1.12 – 1.14 содержат производную экспериментальной функции x ( ), а это приводит к увеличению погрешности вычислений. Поэтому необходимо сгладить экспериментальные данные с помощью некоторой общей процедуры сглаживания. Поскольку такие важные характеристики ММР, как моменты, можно определить непосредственно из I(М), целесообразнее вычислять непосредственно I(М) вместо f (М) либо по 1.10, либо по 1.9, а затем, при необходимости, найти f(M) дифференцированием.

---

Для проверки эффективности нового метода были проведены расчеты для модельных полимеров, подчиняющихся функции распределения Тунга





где р — отношение молярных объемов полимера и растворителя (количество, аналогичное степени полимеризации или М), р_w — средневесовое р, z — параметр распределения и Г (х) является гамма-функцией. Введем новую переменную t и функцию (t) с помощью



Тогда соответствующая функция (t) имеет вид



В качестве модельной функции разрешимости используем растворимость в приближении Скотта



где , и χ связаны соотношением





Наконец, метод требует знания х (χ), воспользуемся усовершенствованной формулой Скотта



Наша задача состоит в том, чтобы вычислить (t) с помощью предложенного алгоритма и сравнить его с результатами метода Рейнера и с первоначально введенной функцией I (t). Важно, что на получаемые таким образом оценки эффективности отдельных методов не влияет выбор ММР, функции разрешимости модели и точность формулы 1.22, поскольку решаемая задача является самосогласованной.

Кривые осадков х(χ) рассчитаны для трех модельных ММР, имеющих параметр неоднородность Шульца U=p

---

_w,/p_n, равный ∞, 2 и 1,11 соответственно (рисунок 1); значения величин с_о = 10^-4 и р_w = 10³ выбраны так, чтобы они соответствовали типичным условиям, встречающимся при турбидиметрическом титровании. Затем восстанавливали интегральную кривую распределения как с помощью метода Гейнера, так и с помощью алгоритма, определяемого уравнениями 1.8-1.10.

Для трех модельных ММР точные (исходные) функции (t) приведены на рисунке 1.8 вместе с функциями (t) и (t), восстановленными соответственно методом Рейнера и по новой методике. Относительные погрешности соответствующих методов решения обратной задачи, также нанесены.





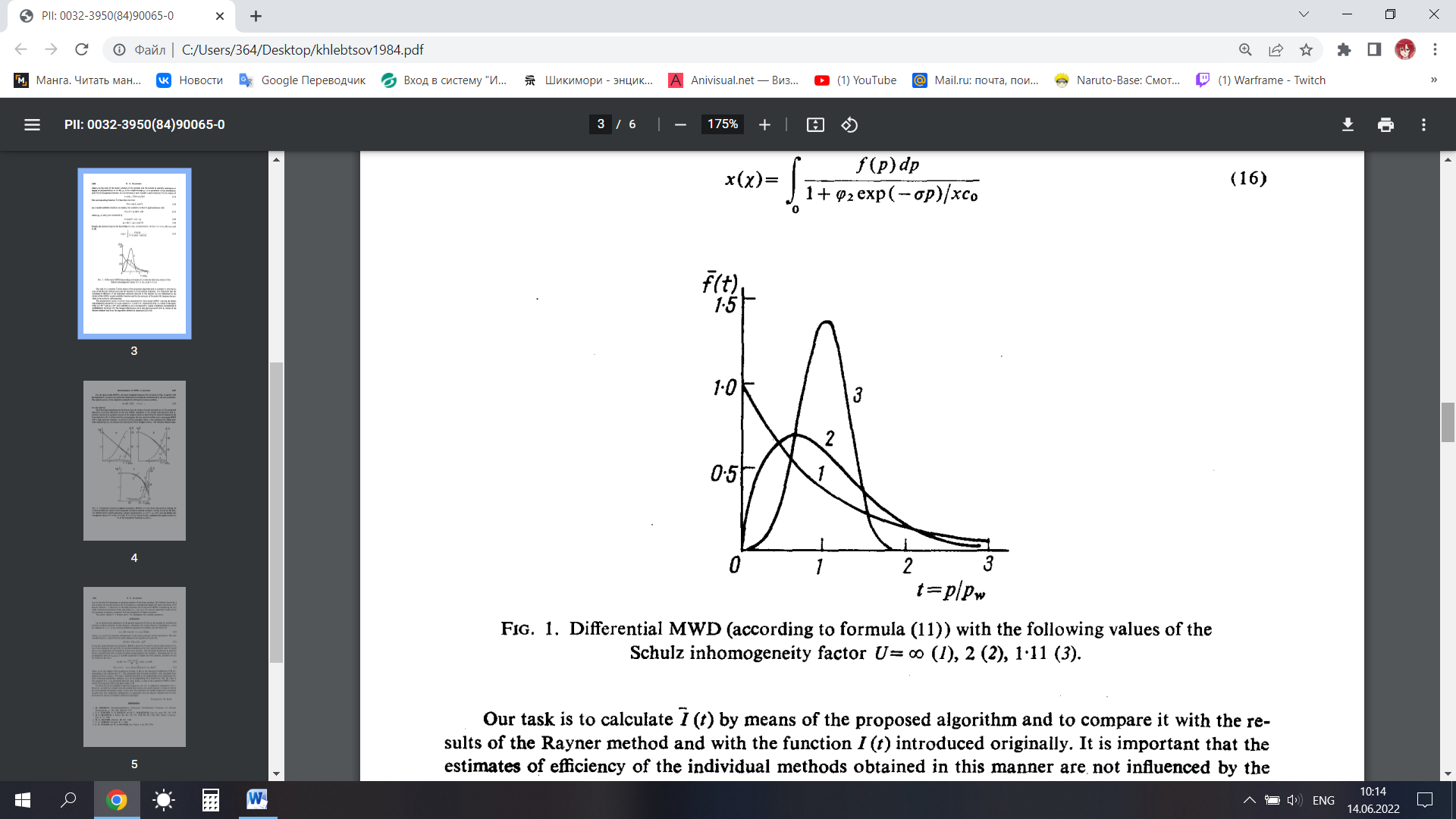
Рисунок 1.7 – Дифференциальное ММР со следующими значениями коэффициента неоднородности Шульца U= ∞ (1), 2 (2), 1,11 (3)



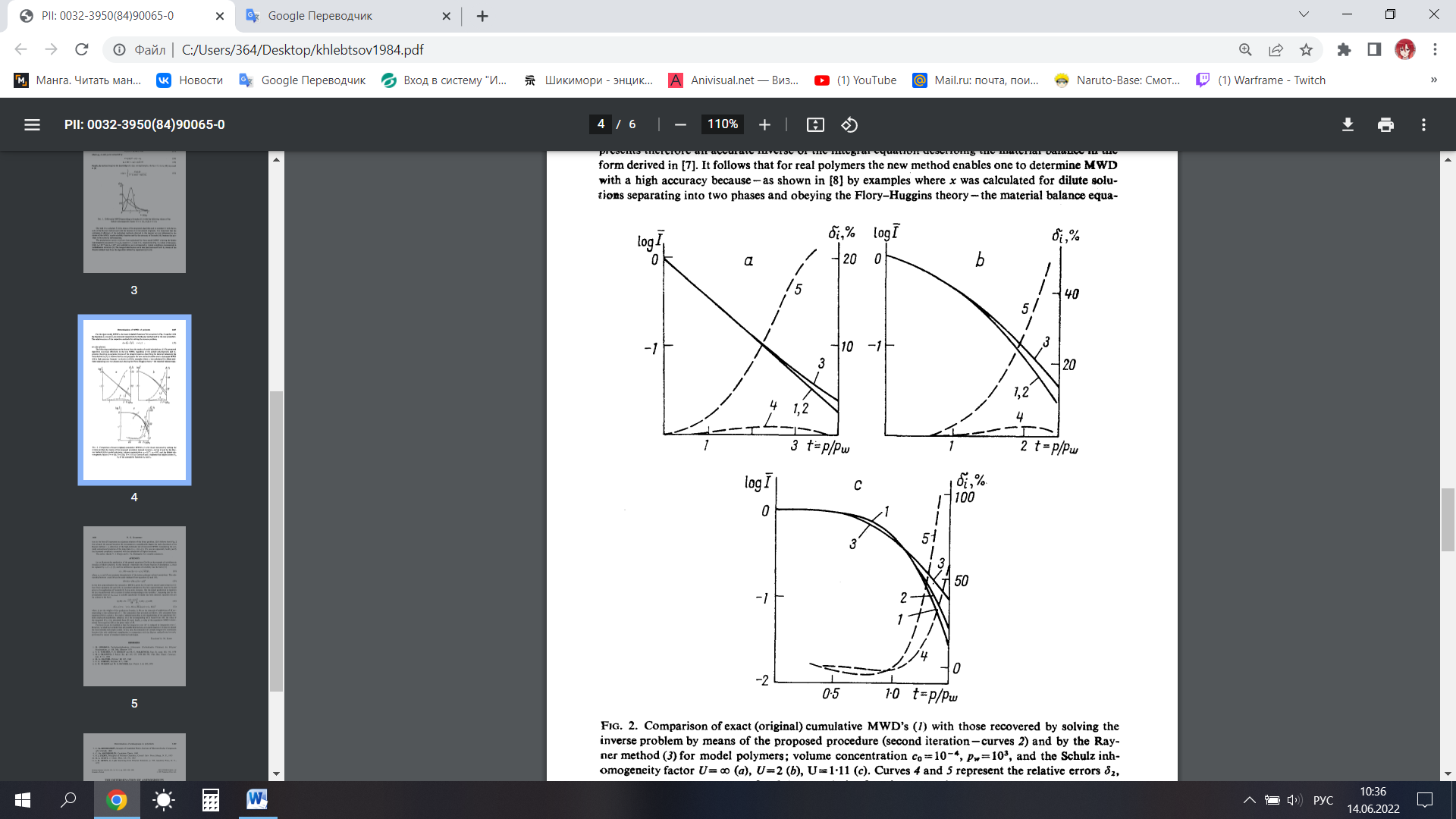
Рисунок 1.8 – Сравнение точных (исходных) кумулятивных ММР (1) с восстановленными при решении обратной задачи по предложенной методике (вторые итерации - кривая 2) и по методу Райхера (3) для модельных полимеров; объемная концентрация с₀=10^-4, p_w=10³, фактор неоднородности Шульца U = ∞ (а), U=2 (b), U=1,11 (c). Кривые 4 и 5 представляют относительные погрешности интегральных функций I₂ и I₁

---

1.4 Заключение по литературному обзору

Молекулярно-массовые распределения, определенные методами преципитационной хроматографии, гель-проникающей хроматографии и методами скорости осаждения, суммированы на рисунках 1.4 – 1.6 для сравнения друг с другом, а также для сравнения с истинными молекулярно-массовыми распределениями, рассчитанными по распределениям составляющих компонентов в смеси. На рисунке 1.4 показан пример для монодисперсного полимера № 4, а на рисунках 1.5 и 1.6 показаны результаты экспериментов для смешанных образцов № 9 и 11. Из этих рисунков мы можем заключить, что как метод преципитационной хроматографии, так и метод седиментации показывают двойные пики намного лучше, чем метод гель-проникающей хроматографии. Кроме того, метод скорости седиментации, по-видимому, имеет несколько более высокое разрешение, чем метод колоночного фракционирования. Гель-проникающая хроматография дает слишком широкое молекулярно-массовое распределение для монодисперсных полимеров, если не делать поправку на эффект уширения. Однако настоящие экспериментальные результаты не обязательно означают, что разрешение ГПХ ниже, чем у других методов, когда образцы являются полидисперсными.

По результатам модельных расчетов можно сделать следующие выводы. Предложенный алгоритм эффективно сходится к истинному MМР независимо от полидисперсности образца и, таким образом, представляет собой точное обращение интегрального уравнения, описывающего материальный баланс. Отсюда следует, что для реальных полимеров новый метод позволяет определять ММР с высокой точностью, поскольку, как показано на примерах, где x рассчитан для разбавленных растворов, разделяющихся на две фазы и подчиняющихся теории Флори-Хаггинса, материальный баланс представляет собой точное решение прямой задачи.

Из рисунка 1.8 следует, что уже вторая итерация (уравнение 1.10) в значительной степени преодолевает основной недостаток метода Рейнера - искажение высокомолекулярного хвоста восстановленного ММР. Учитывая редко встречающуюся точность входных данных (т. е. х(γ), с(γ), М), вряд ли можно оправдать повышенную сложность, связанную с вычислением более высоких итераций.

---

2 Оценить измененение жесткости макромолекул поли[этиленгликольтерефталат – со- парафенилентерефталат] при варьировании его мономерного состава, а также изменение плотности упаковки, растворимости, пористости, температур агрегатных и фазовых переходов

2.1 Расчет коэффициента упаковки

Плотность упаковки количественно оценивается так называемым коэффициентом упаковки, К, который для каждого из мономеров в сополимере можно определить по формуле:

К= 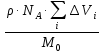(2.1)

где



плотность полимера:

для полиэтиленгликольтерефталата ;[9]

для парафенилентерефталата ;[10]

- молекулярная масса звена.

Определим ван-дер-ваальсов объем компонентов в сополимере:

_(∑∆????)₁=8⋅∆????_????,128+∆????_????,133⋅2+∆????_O,143⋅2+∆????_????,16⋅4+∆????_C,50+∆????_C,15⋅2+∆????_????,47=2⋅₈₊₂⋅<sub>3,4+

+2</sub>⋅_5,85+2⋅_16,2+4⋅_13,1+15,7+2⋅<sub>9+12,5=165,5А3

(∑∆</sub>????)₂=8⋅∆????_????,128+∆????_????,133+∆????_O,143⋅2+∆????_????,16⋅4+∆????_C,50⋅2₊∆????_C,15⋅2+∆????_????,40+∆????_????,10=8⋅_2++3,4+2⋅_5,85+16,2+4⋅_13,1+2⋅_15,7+2⋅_{9+16,2+13,1=162,2А3}

Коэффициент упаковки полиэтиленгликольтерефталата составит:

0,731

Коэффициент упаковки полиэтиленгликольтерефталата составит:

0,771

Коэффициент упаковки сополимера в зависимости от мономерного композиционного состава определим по формуле:

---

Смотрите также файлы

• Вопросы по охране труда.docx

• Лабораторная работа 1. Особенности процесса управления программным проектом Методологии управления итпроектами.docx

• Лабораторная работа Разработка абстрактного базового класса 3 Лабораторная работа Параллелизм и потоки 7.docx

• Фотоэффект. Уравнение Эйнштейна.docx

• Аналитики осуществляют финансовый анализ и внешний, и внутренний внутренний внешний.doc