МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное бюджетное образовательное учреждение высшего образования

«Тольяттинский государственный университет»
Институт инженерной и экологической безопасности

(наименование института полностью)

Институт инженерной и экологической безопасности

(Наименование учебного структурного подразделения)

20.03.01 Техносферная безопасность

(код и наименование направления подготовки / специальности)

Безопасность технологических процессов и производств

(направленность (профиль) / специализация)

Практическое задание № 1
по учебному курсу « Высшая математика 1 »

^{(наименование учебного курса)}
Вариант 5 (при наличии)

Обучающегося	Н.П.Демура
	(И.О. Фамилия)
Группа	ТБбп-2002ас
Преподаватель	Е.А.Курьянова
	(И.О. Фамилия)

Тольятти 2023
Линейная алгебра.

Задача 1.

---

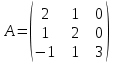
Составляем систему для определения координат собственных векторов:
(2 - λ)x₁ + 1x₂ + 0x₃ = 0
1x₁ + (2 - λ)x₂ + 0x₃ = 0
-1x₁ + 1x₂ + (3 - λ)x₃ = 0
Составляем характеристическое уравнение и решаем его.

2 - λ 1 0 1 2 - λ 0 -1 1 3 - λ

Для этого находим определитель матрицы и приравниваем полученное выражение к нулю.
(2 - λ) • ((2 - λ) • (3 - λ)-1 • 0)-1 • (1 • (3 - λ)-1 • 0)+(-1 • (1 • 0-(2 - λ) • 0)) = 0
После преобразований, получаем:
-λ³+7λ²-15λ+9 = 0

λ₁ = 1
Подставляя λ₁ = 1 в систему, имеем:

2 – 1 1 0 1 2 - 1 0 -1 1 3 - 1

или

1 1 0 1 1 0 -1 1 2

Решаем эту систему линейных однородных уравнений.

---

Выпишем основную матрицу системы:

1 1 0 1 1 0 -1 1 2 x1 x2 x3

Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы.
В матрице B 1-ая и 2-ая строки пропорциональны, следовательно, одну из них, например 1-ю, можно вычеркнуть. Это равносильно вычеркиванию 1-го уравнения системы, так как оно является следствием 2-го.

1 1 0 -1 1 2

Добавим 2-ую строку к 1-ой:

0 2 2 -1 1 2

Найдем ранг матрицы.

0 2 2 -1 1 2

---

Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), следовательно rang(A) = 2.
Этот минор является базисным. В него вошли коэффициенты при неизвестных x₁,x₂, значит, неизвестные x₁,x₂ – зависимые (базисные), а x₃ – свободные.
Преобразуем матрицу, оставляя слева только базисный минор.

0 2 -2 -1 1 -2

Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:
2x₂ = - 2x₃
- x₁ + x₂ = - 2x₃
Методом исключения неизвестных находим нетривиальное решение:
Получили соотношения, выражающие зависимые переменные x₁,x₂ через свободные x₃, то есть нашли общее решение:


x₂ = - x₃
x₁ = x₃
Множество собственных векторов, отвечающих собственному числу λ₁ = 1, имеет вид:

(x₃,-x₃,x₃) = x₃(1,-1,1)
где x₃ - любое число, отличное от нуля. Выберем из этого множества один вектор, например, положив x₃ = 1:

x₁ = (1,-1,1)

λ₂ = 3
Подставляя λ₂ = 3 в систему, имеем:

2 – 3 1 0 1 2 - 3 0 -1 1 3 - 3

---

или

-1 1 0 1 -1 0 -1 1 0

Решаем эту систему линейных однородных уравнений
Выпишем основную матрицу системы:

-1 1 0 1 -1 0 -1 1 0 x1 x2 x3

---

Смотрите также файлы

• Наука как предмет филофского исследования.docx

• Лабораторная работа 1. по учебному курсу Международное право (наименование учебного курса) Студент.docx

• Задача Прокурор района принес протест на решение районной налоговой инспекции.docx

• Модуль атауы Электрэнергетикалы жйелерді тратылыы Дублин дискрипторлары.docx

• Электромобили в 2022 году реальность и прогнозы специалистов.docx