Файл: IBM_SPSS_Statistics_Base.pdf

87

Расстояния

Рисунок 14-1

Диалоговое окно Расстояния

E

Выберите

,

по крайней мере

,

одну числовую переменную

,

чтобы вычислять расстояния

между наблюдениями

,

или выберите

,

по крайней мере

,

две числовые переменные

,

чтобы

вычислить расстояния между переменными

.

E

Выберите одну из двух альтернатив в группе Вычислить расстояния между

,

чтобы

вычислить расстояния либо между наблюдениями

,

либо между переменными

.

88

Глава 14

Меры различия

Рисунок 14-2

Диалоговое окно Расстояния: Меры различия

В группе Мера выберите альтернативу

,

соответствующую типу данных

(

интервальным

,

частотам или двоичным

);

затем в выпадающем списке выберите одну из мер

,

которая

соответствует этому типу данных

.

Доступными мерами в зависимости от типа данных

являются следующие

:



Интервальные данные.

Расстояние Евклида

,

квадрат расстояния Евклида

,

расстояние

Чебышева

,

блок

,

Минковского или Настроенная

(

пользователем

).



Частоты.

Меры хи

-

квадрат или фи

-

квадрат

.



Двоичные данные.

Расстояние Евклида

,

квадрат расстояния Евклида

,

различие

размеров

,

различие структур

,

дисперсия

,

форма

,

Ланс и Виллиамс

. (

Введите значения

в поля Наличие и Отсутствие

,

чтобы указать

,

какие два значения используются

;

остальные значения будут игнорироваться процедурой

.)

Группа Преобразовать значения позволяет

перед

вычислением близостей стандартизировать

значения данных либо для наблюдений

,

либо для переменных

.

Эти преобразования

неприменимы к бинарным данным

.

Возможные методы стандартизации

:

Z

значения

,

Диапазон от

–1

до

1,

Диапазон от

0

до

1,

Максимальная величина

1,

Среднее

1

и Стд

.

отклонение

1

Группа Преобразовать меры позволяет преобразовать генерируемые значения меры

расстояния

.

Преобразования выполняются после того

,

как вычислены значения меры

расстояния

.

Доступные преобразования

:

взятие модуля

,

смена знака

,

приведение к

диапазону

0–1.

89

Расстояния

Меры сходства

Рисунок 14-3

Диалоговое окно Расстояния: Меры сходства

В группе Мера выберите альтернативу

,

соответствующую типу данных

(

интервальная или

двоичная

);

затем в выпадающем списке выберите одну из мер

,

которая соответствует этому

типу данных

.

Доступными мерами в зависимости от типа данных являются следующие

:



Интервальные данные.

Коэффициент корреляции Пирсона или косинус

.



Двоичные данные.

Рассел и Рао

,

простая мера совпадений

,

Жаккар

,

дайс

,

Роджерс

и Танимото

,

Сокал и Сниат

1,

Сокал и Сниат

2,

Сокал и Сниат

3,

Кульчинский

1,

Кульчинский

2,

Сокал и Сниат

4,

Хаманн

,

Лямбда

,

D

Андерберга

,

Y

Юла

,

Q

Юла

,

Очиай

,

Сокал и Сниат

5,

четырехточечная корреляция фи

,

разброс

. (

Введите значения в поля

Наличие и Отсутствие

,

чтобы указать

,

какие два значения используются

;

остальные

значения будут игнорироваться процедурой

.)

Группа Преобразовать значения позволяет перед вычислением расстояний
стандартизировать значения данных либо для наблюдений

,

либо для переменных

.

Эти

преобразования неприменимы к бинарным данным

.

Возможные методы стандартизации

:

Z

значения

,

Диапазон от

–1

до

1,

Диапазон от

0

до

1,

Максимальная величина

1,

Среднее

1

и

Стд

.

отклонение

1

Группа Преобразовать меры позволяет преобразовать генерируемые значения меры

расстояния

.

Преобразования выполняются после того

,

как вычислены значения меры

расстояния

.

Доступные преобразования

:

взятие модуля

,

смена знака

,

приведение к

диапазону

0–1.

Команда PROXIMITIES: дополнительные возможности

Процедура Расстояния использует синтаксис команды

PROXIMITIES

.

Язык синтаксиса

команд также позволяет

:



Задать любое целое число в качестве степени для меры расстояния Минковского

.



Задать любое целое число в качестве корня для настраиваемой меры расстояния

.

90

Глава 14

Полную информацию о синтаксисе языка команд можно найти в

Руководстве по

синтаксису

.

Глава

15

Линейные модели

Линейные модели предсказывают значения непрерывных целевых переменных

,

основываясь на взаимосвязи между целевой переменной и одним или несколькими
предикторами

.

Линейные модели относительно просты и дают легко интерпретируемую математическую
формулу для скоринга

.

Свойства этих моделей хорошо понятны

,

и их обычно можно

построить очень быстро

,

по сравнению с моделями других типов

(

такими как нейронные

сети или деревья решений

)

на том же наборе данных

.

Пример.

Страховая компания с ограниченными ресурсами для исследования страховых

требований домовладельцев желает построить модель для оценки стоимости требований

.

Применяя эту модель в центрах обслуживания

,

сотрудники компании могут ввести

информацию от требовании

,

разговаривая по телефону с клиентом

,

и немедленно получить

“

ожидаемую

”

стоимость требования

,

основываясь на прошлых данных

.

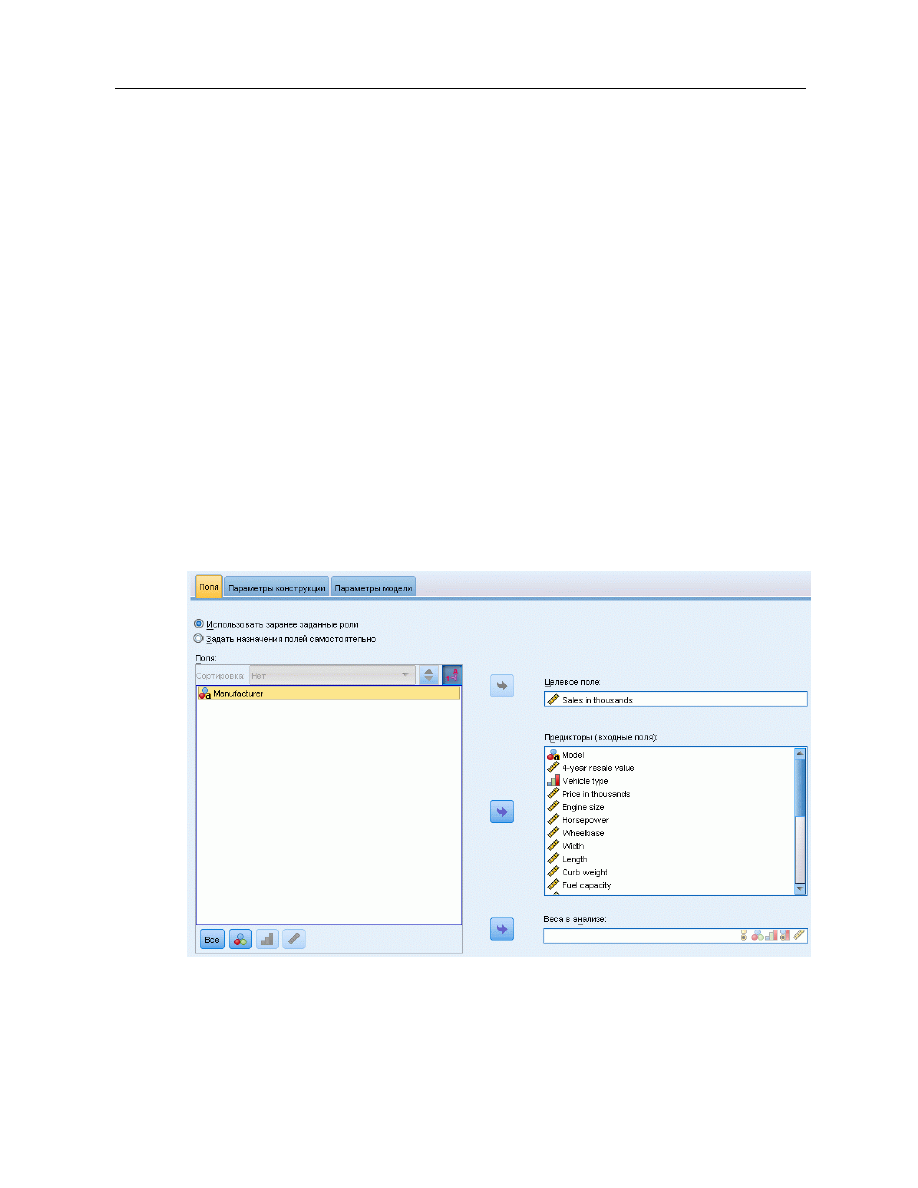
Рисунок 15-1

Вкладка Поля

Требования к полям.

Должны быть целевое и

,

по крайней мере

,

одно входное поля

.

По

умолчанию не используются поля с предопределенными ролями Двойного назначения
и Нет

.

Целевое поле должно быть непрерывным

(

количественным

).

Для предикторов

(

входные

)

отсутствуют ограничения на тип измерений

;

категориальные

(

номинальные

© Copyright IBM Corporation 1989, 2011.

91