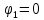, остаются неизвестными потенциалы узлов “2”,“3”.

Выразим токи 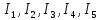в ветвях через потенциалы, выбирая предварительно их условные положительные направления, как показано на рис.2.1, и подставим заданные значения сопротивлений: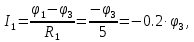











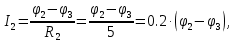
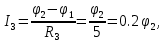
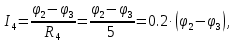
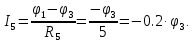
Составим уравнения для узлов “1”,“2” по 1-му закону Кирхгофа:

Узел «1»: ,

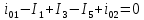Узел «2»:

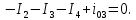
Подставим в уравнения по закону Кирхгофа выражения для токов, заданные через потенциалы . Запишем систему уравнений.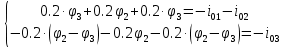



Упростим выражения в системе уравнений:



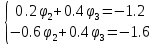
Решим систему линейных уравнений относительно неизвестных .

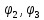Отнимем из 1-го уравнения системы 2-е уравнение системы и вычислим значение :



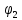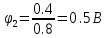
Подставим значение 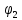в 1-е уравнение системы и определим значение :



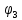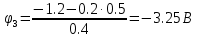
Определим значения токов, подставив в выражения для них найденные значения потенциалов.

---

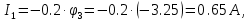
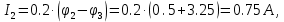
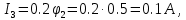
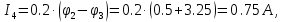
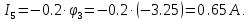
Сделаем проверку найденных значений токов по первому закону Кирхгофа для независимых узлов цепи.

Узел «1»: ,

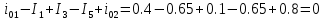Узел «2»:

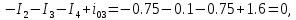
Узел «3»:

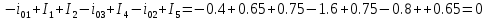
Проверка подтвердила правильность расчетов.

Задача 3

Расчёт линейной цепи с одним независимым источником гармонических колебаний методом комплексных амплитуд
Для цепи, схема которой приведена в табл. 3.1, рассчитайте ток или напряжение на зажимах источника напряжения или тока, комплексную мощность на зажимах источника, определите среднюю и реактивную мощности источника.

Для этого:

1. 
   Перерисуйте схему и замените заданное гармоническое колебание ????0 (????) или ????0 (????) соответствующей комплексной амплитудой.
   
2. 
   Запишите комплексные сопротивления элементов цепи.
   
3. 
   Найдите общее комплексное сопротивление относительно зажимов источника.
   
4. 
   Применяя закон Ома в комплексной форме, вычислите комплексную амплитуду тока через источник напряжения или комплексную амплитуду напряжения на зажимах источника тока.
   
5. 
   Запишите мгновенное значение тока через источник напряжения или напряжения на зажимах источника тока.
   
6. 
   Найдите комплексную мощность на зажимах источника, определите среднюю и реактивную мощности источника.
   

Таблица 3.1. Схема электрической цепи и исходные данные

Вариант	Схема	Исходные данные
В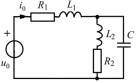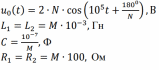

Дано:

---

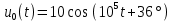
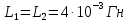
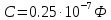
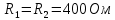
Найти:


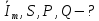
Решение:



Рис.3.1. Схема электрической цепи

Заменим заданное гармоническое колебание ????0(????) соответствующей комплексной амплитудой:



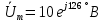
Определим реактивные сопротивления участков цепи:







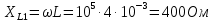
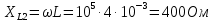
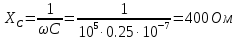
Запишем комплексные сопротивления ветвей:







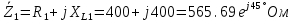
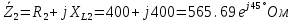
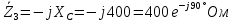
Вычислим общее сопротивление 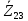сопротивлений 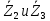, соединенных параллельно: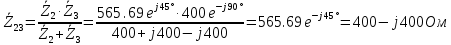



Находим эквивалентное сопротивление всей цепи, как последовательное соединение сопротивлений :



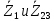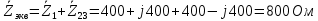
Вычислим комплексный ток 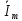по закону Ома: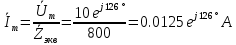





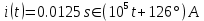
Вычислим полную комплексную мощность:



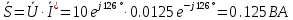
Отсюда: , .

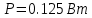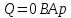Задача 4

Определение комплексной передаточной функции цепи 1-го порядка. Построение амплитудно-частотных и фазочастотных характеристик

Найдите комплексную передаточную функцию ????(????ω) цепи 1-го порядка и определите по ней частотные характеристики: амплитудночастотную |????(????????)| и фазочастотную ϴ(????).

---

Для этого:

1. 
   Выберите для своего варианта схему пассивной RL или RC цепи из табл. 4.1 и рассчитайте значения её параметров через M и N.
   
2. 
   Найдите требуемую комплексную передаточную функцию ????(????ω) указанного вида в общем виде через её параметры R, L, C: ????(????ω) = |????(????????)| ∙ .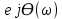
   
3. 
   Запишите в общем виде через параметры R, L, C выражения для амплитудно-частотной |????(????????)| и фазочастотной ϴ(????) характеристик. Постройте качественные графики АЧХ и ФЧХ, определив значения частотных характеристик при ω = 0 и ω → ∞.
   
4. 
   На графике АЧХ покажите полосу пропускания и определите граничную частоту полосы пропускания .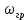
   

Таблица 4.1. Схема электрической цепи и исходные данные

Вариант	Схема	Исходные данные
В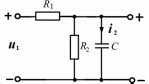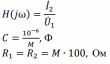

Дано:







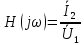
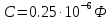
Найти:



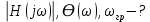
Решение:

Переходим к схеме замещения цепи для комплексных действующих значений токов и напряжений:



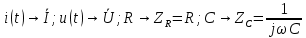
Запишем уравнение по 1-у закону Кирхгофа:



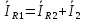
Запишем уравнения по второму закону Кирхгофа:





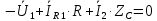
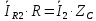
Выразим ток 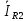через ток :



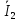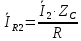
Выразим ток

---

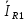
в неразветвленной части цепи через ток :



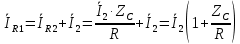
И подставим в уравнение по 2-у закону Кирхгофа:



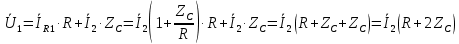
Тогда:



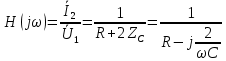
АЧХ:



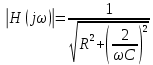
ФЧХ:



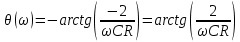
Определим значения частотных характеристик при ω = 0 и ω → ∞:

При ω = 0 конденсатор представляет из себя разрыв, значит ток через него не течет:



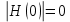
При ω → ∞ конденсатор представляет из себя короткое замыкание, значит весь ток цепи протекает через него:



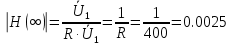
Найдем граничную частоту полосы пропускания:









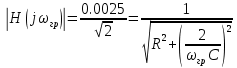
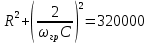
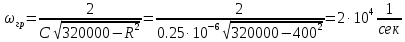
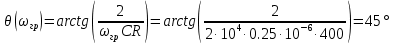
На рис. 4.1 и 4.2 приведены графики АЧХ и ФЧХ, рассчитанные по полученным формулам.



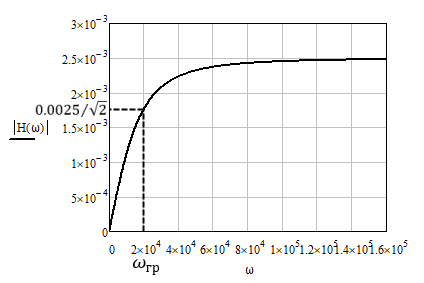
Рис.4.1 График АЧХ



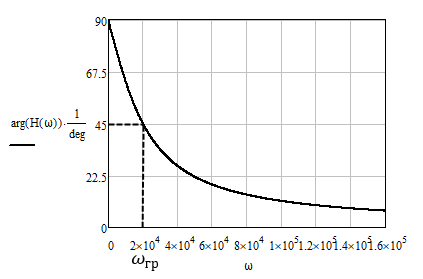
Рис.4.2 График ФЧХ

Задача 5

Анализ переходных колебаний в электрической цепи классическим методом

Найдите закон изменения напряжения и тока на реактивном элементе ???????? (????), ???????? (????) или ???????? (????), ???????? (????) после коммутации при условии, что до коммутации в цепи был установившийся режим.

Для этого:

1. 
   Выберите для своего варианта схему цепи и рассчитайте её параметры через M и N из табл. 5.1, если последняя цифра номера зачётной книжки нечётная.
   
2. 
   Составьте для схемы, получившейся после коммутации, систему уравнений по законам Кирхгофа для мгновенных значений токов и напряжений и получите одно дифференциальное уравнение относительно ???????? (????) или ???????? (????).
   
3. 
   Найдите путём решения полученного дифференциального уравнения искомую реакцию цепи ???????? (????) или ???????? (????), по которой определите ???????? (????) или ???????? (????) соответственно.
   
4. 
   Постройте графики функций ???????? (????), ???????? (????) или ???????? (????), ???????? (????).
   

---

Смотрите также файлы

• Программа лагеря с дневным пребыванием Солнышко паспорт программы.doc

• 1. Составляется список факторов, влияющих на размещение производства.docx

• Амола облысы білім басармасыны Аршалы ауданы бойынша білім блімі Волгодоновка ауылыны жалпы орта білім беретін мектебі кмм таырыбы.docx

• Ответ Интеграция.docx

• Лабораторная работа 1 тема составление литологостратиграфического разреза и построение схемы сопоставления (корреляции) отложений.pdf