Файл: Содержание введение 3 глава основы теории и вопросы моделирования.docx
Добавлен: 09.11.2023
Просмотров: 966
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, размеры которого (которой) пренебрежимо малы по сравнению с расстояниями до других зарядов рассматриваемой системы. Точечный заряд такая же физическая идеализация, как и материальная точка в механике. Пробным зарядом называется положительный точечный заряд, который вносится в данное электромагнитное поле для измерения его характеристик. Этот заряд должен быть достаточно мал, чтобы не нарушать положение зарядов–источников измеряемого поля и тем самым, не искажать существующее поле. Таким образом, пробный заряд служит индикатором электромагнитного поля (точнее, покоящийся пробный заряд является индикатором электрического поля). Основные свойства электрического заряда [1]:
????=1
???? = ????1 + ????2 + ????3 + ⋯ = ∑???? ????????; (1.1)
Закон Кулона был открыт в 1785 г. Ш. Кулоном и позволяет рассчитать силу взаимодействия двух неподвижных точечных зарядов ????1и????2:
4????????????0????3
????⃗12 = − ????1????2????⃗12 . (1.2)
12
На основе обобщения опытных данных М. Фарадеем в 1843 сформулирован следующий закон сохранения заряда. Заряд электрически замкнутой системы (через поверхность которой не переносятся заряженные частицы) не изменяется, какие бы процессы в ней не происходили. Следствие из этого закона: если зарядовая система 1 отдает заряд системе 2, то система 2 получает ровно
такой заряд, какой теряет система 1.
Закон релятивистская инвариантность заряда, сформулированный Г. Лоренцем в 1877 г. также на экспериментальной основе, гласит: заряд любого тела инвариантен относительно изменения системы отсчета. Следствие из этого за- кона: заряд тела не зависит от его скорости и ускорения.
Можно указать следующие процессы возникновения и исчезновения свободных зарядов:
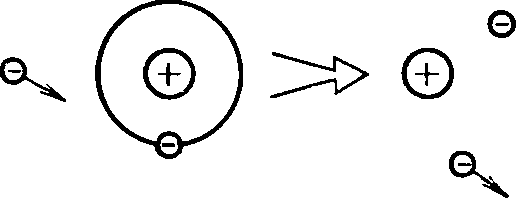
Рис. 1. Пример процесса столкновительной ионизации атом-электрон

Рис. 2. Пример столкновения гаммаквантов
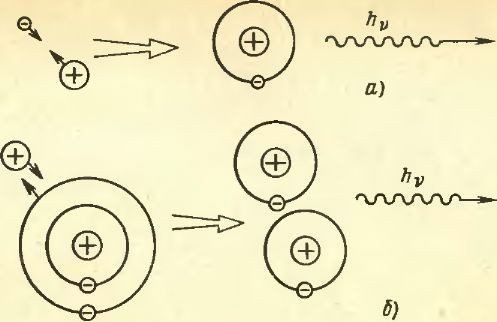
Рис. 3. Пример рекомбинации
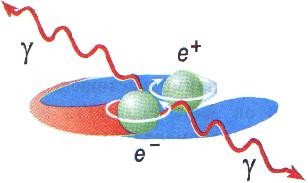
Рис. 4. Пример «уничтожения» пары электрон-позитрон
Согласно закону Кулона, сила взаимодействия двух неподвижных точечных зарядов прямо пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними (рис. 5.)
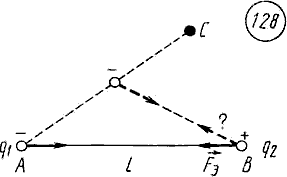
Рис. 5.
В каждой точке пространства, где есть электромагнитное поле, на пробный заряд q действует определенная сила, зависящая (при заданных зарядах- источниках поля) от величины пробного заряда и его положения относительно источников. При фиксированной величине заряда q, покоящегося в заданном электростатическом поле, эта сила зависит только от его координат (x,y,z). Напряженностью электрического поля называется сила, действующая со стороны электромагнитного поля на заряд q, покоящийся в точке (x,y,z), отнесенная к величине этого заряда:
????(????, ????, ????) = ????????(????,????,????). (1.3)
????
Формула (1.3) дает определение напряженности электростатического поля, если известно, что заряды – источники поля также покоятся. Зная Е как функцию координат нетрудно найти силу, действующую в данном поле на данный заряд в любой точке:
???????? = ????????. (1.4)
Из закона Кулона и определения (1.4) следует, что напряженность электро статического поля, созданного точечным зарядом Q на расстоянии r от него равна

????3
???? = ???????? ????????. (1.5)
Электрическое поле можно задавать графически с помощью линий напряжённости.
Линия напряжённости электрического поля– это линия, в любой точке ко- торой вектор напряжённости направлен по касательной к ней. Линии напряжённости электрического поля точечного заряда представляют собой прямые линии, идущие от положительного заряда или к отрицательному заряду (рис. 1.6). Свойства электростатических силовых линий вытекают из этого определения, формулы для напряженности поля точечного заряда (1.5) и принципа суперпозиции.
Силовые линии электростатического поля не бывают замкнутыми, не пересекаются вне зарядов, начинаются на положительных зарядах и заканчивают ся на отрицательных или уходят в бесконечность.
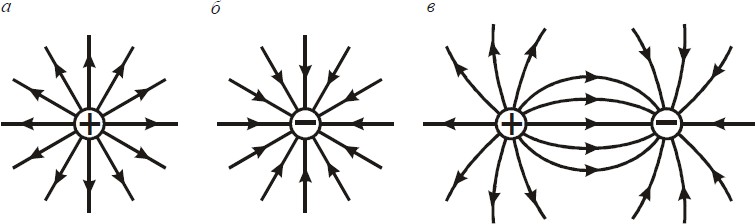
Рис. 6. Линии напряженности поля положительного (а), отрицательного (б) зарядов и системы из двух зарядов разного знака (в)
Для напряжённости электрического поля выполняется принцип суперпозиции [1]: каждый электрический заряд в данной точке пространства создаёт электрическое поле вне зависимости от наличия других электрических зарядов.
Поскольку электростатическое поле создается, в конечном счете, точечными зарядами (любое заряженное тело можно рассматривать как систему микроскопических заряженных частиц), то сила, действующая на пробный за- ряд со стороны произвольного электростатического поля, есть сумма сил, действующих на пробный заряд со стороны каждого точечного источника. Отсюда следует принцип суперпозиции, который можно выразить формулой для суммы полей точечных зарядов в точке, удаленной на расстояния от них:
???? = ∑
????
????=1
???????? = ∑????
???????? ???????? ???????? (1.6)
????3
????=1
????
Если расстояние от каждого из зарядов до точки наблюдения много больше расстояний между зарядами, то во многих случаях формулу (1.4) можно приближенно заменить формулой (1.5), где Q –суммарный заряд системы, а r – расстояние от какой-либо точки внутри системы зарядов. При этом, если Q = 0, т.е. система зарядов электрически нейтральна, поле вдали от системы практически отсутствует. Именно поэтому большинство тел
, хоть и содержит множество заряженных частиц, не создают поля.
-
дискретность (любой заряд всегда кратен элементарному заряду)q=N׀e׀, где N– целое число; -
аддитивность (заряд системы заряженных тел равен алгебраической сумме зарядов отдельных тел)
????=1
???? = ????1 + ????2 + ????3 + ⋯ = ∑???? ????????; (1.1)
-
суммарный заряд электрически изолированной системы, через границы, которой не могут проникать заряженные частицы, с течением времени не изменяется (закон сохранения электрического заряда), Q=const; -
инвариантность (величина заряда одинакова во всех инерциальных системах отсчета).
Закон Кулона был открыт в 1785 г. Ш. Кулоном и позволяет рассчитать силу взаимодействия двух неподвижных точечных зарядов ????1и????2:
4????????????0????3
????⃗12 = − ????1????2????⃗12 . (1.2)
12
На основе обобщения опытных данных М. Фарадеем в 1843 сформулирован следующий закон сохранения заряда. Заряд электрически замкнутой системы (через поверхность которой не переносятся заряженные частицы) не изменяется, какие бы процессы в ней не происходили. Следствие из этого закона: если зарядовая система 1 отдает заряд системе 2, то система 2 получает ровно
такой заряд, какой теряет система 1.
Закон релятивистская инвариантность заряда, сформулированный Г. Лоренцем в 1877 г. также на экспериментальной основе, гласит: заряд любого тела инвариантен относительно изменения системы отсчета. Следствие из этого за- кона: заряд тела не зависит от его скорости и ускорения.
Можно указать следующие процессы возникновения и исчезновения свободных зарядов:
-
ионизация при столкновении атома с электроном приводит формированию положительно и отрицательно заряженных частиц (см. пример на рис. 1);

Рис. 1. Пример процесса столкновительной ионизации атом-электрон
-
рождение электрона и позитрона при столкновении гаммаквантов:

Рис. 2. Пример столкновения гаммаквантов
-
рекомбинация иона и электрона:

Рис. 3. Пример рекомбинации
-
аннигиляция пары электрон-позитрон:

Рис. 4. Пример «уничтожения» пары электрон-позитрон
Согласно закону Кулона, сила взаимодействия двух неподвижных точечных зарядов прямо пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними (рис. 5.)

Рис. 5.
- 1 2 3 4 5 6 7 8 9 ... 12
1.2. Напряженность электрического поля
В каждой точке пространства, где есть электромагнитное поле, на пробный заряд q действует определенная сила, зависящая (при заданных зарядах- источниках поля) от величины пробного заряда и его положения относительно источников. При фиксированной величине заряда q, покоящегося в заданном электростатическом поле, эта сила зависит только от его координат (x,y,z). Напряженностью электрического поля называется сила, действующая со стороны электромагнитного поля на заряд q, покоящийся в точке (x,y,z), отнесенная к величине этого заряда:
????(????, ????, ????) = ????????(????,????,????). (1.3)
????
Формула (1.3) дает определение напряженности электростатического поля, если известно, что заряды – источники поля также покоятся. Зная Е как функцию координат нетрудно найти силу, действующую в данном поле на данный заряд в любой точке:
???????? = ????????. (1.4)
Из закона Кулона и определения (1.4) следует, что напряженность электро статического поля, созданного точечным зарядом Q на расстоянии r от него равна

????3
???? = ???????? ????????. (1.5)
Электрическое поле можно задавать графически с помощью линий напряжённости.
Линия напряжённости электрического поля– это линия, в любой точке ко- торой вектор напряжённости направлен по касательной к ней. Линии напряжённости электрического поля точечного заряда представляют собой прямые линии, идущие от положительного заряда или к отрицательному заряду (рис. 1.6). Свойства электростатических силовых линий вытекают из этого определения, формулы для напряженности поля точечного заряда (1.5) и принципа суперпозиции.
Силовые линии электростатического поля не бывают замкнутыми, не пересекаются вне зарядов, начинаются на положительных зарядах и заканчивают ся на отрицательных или уходят в бесконечность.

Рис. 6. Линии напряженности поля положительного (а), отрицательного (б) зарядов и системы из двух зарядов разного знака (в)
Для напряжённости электрического поля выполняется принцип суперпозиции [1]: каждый электрический заряд в данной точке пространства создаёт электрическое поле вне зависимости от наличия других электрических зарядов.
Поскольку электростатическое поле создается, в конечном счете, точечными зарядами (любое заряженное тело можно рассматривать как систему микроскопических заряженных частиц), то сила, действующая на пробный за- ряд со стороны произвольного электростатического поля, есть сумма сил, действующих на пробный заряд со стороны каждого точечного источника. Отсюда следует принцип суперпозиции, который можно выразить формулой для суммы полей точечных зарядов в точке, удаленной на расстояния от них:
???? = ∑
????
????=1
???????? = ∑????
???????? ???????? ???????? (1.6)
????3
????=1
????
Если расстояние от каждого из зарядов до точки наблюдения много больше расстояний между зарядами, то во многих случаях формулу (1.4) можно приближенно заменить формулой (1.5), где Q –суммарный заряд системы, а r – расстояние от какой-либо точки внутри системы зарядов. При этом, если Q = 0, т.е. система зарядов электрически нейтральна, поле вдали от системы практически отсутствует. Именно поэтому большинство тел
, хоть и содержит множество заряженных частиц, не создают поля.
- 1 2 3 4 5 6 7 8 9 ... 12