Файл: Содержание введение 3 глава основы теории и вопросы моделирования.docx
Добавлен: 09.11.2023
Просмотров: 959
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1.5. Потенциал
Напряженность Е является силовой характеристикой электрического поля, т.к. определяет силу, действующую на электрический заряд, находящийся в поле E. Однако часто легче исследовать свойства системы, рассматривая энергии, а не силы. С этой целью в электромагнетизме вводится понятие электрического потенциала V(r), определяемого соотношением:
????1
или
????(????2) − ????(????1) = − ∫????2 ????????????
(1.16)
????(????) = −∇????(????). (1.17)
 ∇= ????
∇= ????????????
???? + ????
 ????????
???????????? + ????
 ????????
????????????, (1.18)
где i, j, k − единичные векторы (орты) соответственно осей x, y, z. В одномер- ном случае формула сводится к E(x) = − dV/ dx, а если потенциал V зависит только от модуля r(сферическая симметрия), то E(r)= − dV/ dr.
Во всех случаях направление вектора Е совпадает с направлением наибо- лее быстрого убывания потенциала, что является общим свойством поля Е.
Потенциал точечного заряда (при условии, что на бесконечности он равен нулю) легко получить, проинтегрировав правую часть в формуле, где Е опреде-
ляется законом Кулона:
 V(r) = q . (1.19)
V(r) = q . (1.19)4π????0r
Поверхность, на которой потенциал принимает одинаковые значения, называется эквипотенциальной поверхностью, которая везде ортогональна си ловым линиям электрического поля. В двумерном случае − это эквипотенци альные линии.
Используя свойство ортогональности эквипотенциальных линий силовым линиям электрического поля можно теперь нарисовать в двумерном случае эквипотенциальные линии. Действительно, если компоненты силовой линии определяются формулами (1.16), то компоненты отрезка, перпендикулярного Е, будут определяться следующими формулами [1]:
∆x = −∆s Ey , ∆y = ∆s Ex. (1.20)
|????| |????|
Таким образом, мы теперь можем, используя тот же алгоритм, что был рассмотрен выше для рисования силовых линий электрического поля, рисовать также эквипотенциальные линии, т.е. моделировать электрическое полеEдля стационарного распределения зарядов.
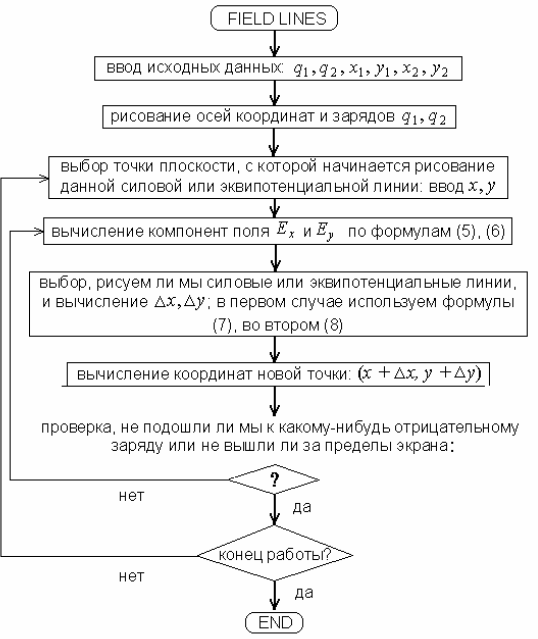 Общая блок-схема алгоритма, реализующего метод, будет выглядеть, как пока- зано на рис. 1.8.
Общая блок-схема алгоритма, реализующего метод, будет выглядеть, как пока- зано на рис. 1.8.Рис.1.8. Блок-схема алгоритма
- 1 2 3 4 5 6 7 8 9 ... 12
ОСНОВЫ ТЕОРИИ И ВОПРОСЫ МОДЕЛИРОВАНИЯ МАГНИТНОГО ПОЛЯ
-
Магнетизм
При прохождении электрического тока по проводнику вокруг него образу- ется магнитное поле. Магнитное поле представляет собой один из видов мате- рии. Оно обладает энергией, которая проявляет себя в виде электромагнитных сил, действующих на отдельные движущиеся электрические заряды (электроны и ионы) и на их потоки, т. е. электрический ток. Под влиянием электромагнит- ных сил движущиеся заряженные частицы отклоняются от своего первоначаль- ного пути в направлении, перпендикулярном полю(рис. 2.1).
Магнитное поле образуется только вокруг движущихся электрических зарядов, и его действие распространяется тоже лишь на движущиеся заряды. Магнитное и электрические поля неразрывны и образуют совместно единое электромаг- нитное поле. Всякое изменение электрического поля приводит к появлению магнитного поля и, наоборот, всякое изменение магнитного поля сопровожда- ется возникновением электрического поля. Электромагнитное поле распро- страняется со скоростью света, т. е. 300 000 км/с.
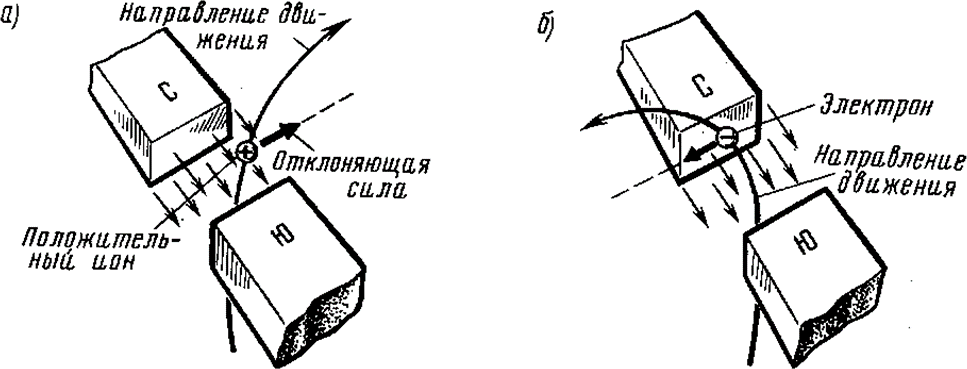
Рис. 2.1. Схемы действия магнитного поля на движущиеся электрические заряды: положительный ион (а) и электрон (б)
2.2Принцип суперпозиции для магнитных полей
Источниками магнитного поля являются движущиеся электрические заряды (токи). Магнитное поле токов принципиально отличается от электрического поля. Магнитное поле, в отличие от электрического, оказывает силовое дей- ствие только на движущиеся заряды (токи). Характеристикой магнитного поля является вектор магнитной индукции, который определяет силы, действующие на токи или движущиеся заряды в магнитном
поле.
За положительное направление вектора принимается направление от южного полюса S к северному полюсу N магнитной стрелки, свободно ориентирую- щийся в магнитном поле. Таким образом, исследуя магнитное поле, создавае- мое током или постоянным магнитом, с помощью маленькой магнитной стрел- ки, можно в каждой точке пространства определить направление вектора.
Направление этого вектора для поля прямого проводника с током и соленоида можно определить по правилу буравчика: если направление поступательного движения буравчика (винта) с правой нарезкой совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направ- лением вектора магнитной индукции.
Модуль индукции B магнитного поля прямолинейного проводника с током I на расстоянии R от него выражается соотношением:
 ???? = ????0 ∗ ???? , (2.1)
???? = ????0 ∗ ???? , (2.1)2???? ????
где μ0 – постоянная величина, которую называют магнитной постоянной. Ее численное значение равно μ0 = 4π∙10–7H/A2 ≈ 1,26∙10–6H/A2.
Принцип суперпозиции магнитных полей: если магнитное поле создано не- сколькими проводниками с токами, то вектор магнитной индукции в какой-
либо точке этого поля равен векторной сумме магнитных индукций, созданных в этой точке каждым током в отдельности (рис. 2.2):
????=1
????�⃗ = ∑????
????�⃗????. (2.2)
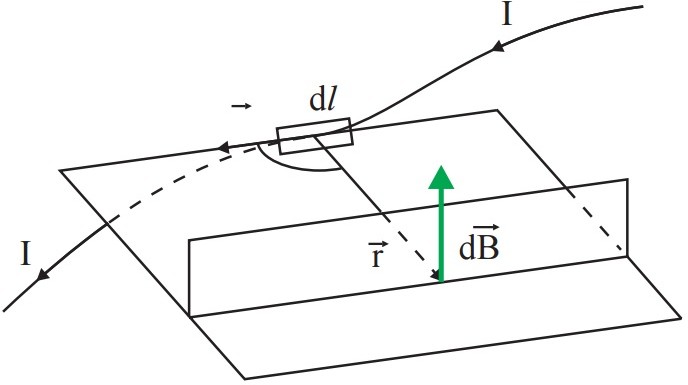
Рис. 2.2. Пример суперпозиции магнитных полей
2.3. Силовые линии магнитного поля
Графически магнитное поле изображают магнитными силовыми линиями, которые проводят так, чтобы направление силовой линии в каждой точке поля совпадало с направлением сил поля; магнитные силовые линии всегда являются непрерывными и замкнутыми. Направление магнитного поля в каждой точке может быть определено при помощи магнитной стрелки. Северный полюс стрелки всегда устанавливается в направлении действия сил поля. Конец посто- янного магнита, из которого выходят силовые линии (рис. 2.3, а), принято счи- тать северным полюсом, а противоположный конец, в который входят силовые линии ˗ южным полюсом (силовые линии, проходящие внутри магнита, не по-
казаны). Распределение силовых линий между полюсами плоского магнита можно обнаружить при помощи стальных опилок, насыпанных на лист бумаги, положенный на полюсы (рис. 2.3, б). Для магнитного поля в воздушном зазоре между двумя параллельно расположенными разноименными полюсами посто- янного магнита характерно равномерное распределение силовых магнитных линий (рис. 2.4) (силовые линии, проходящие внутри магнита, не показаны).

Рис. 2.3. Магнитное поле, созданное постоянным магнитом
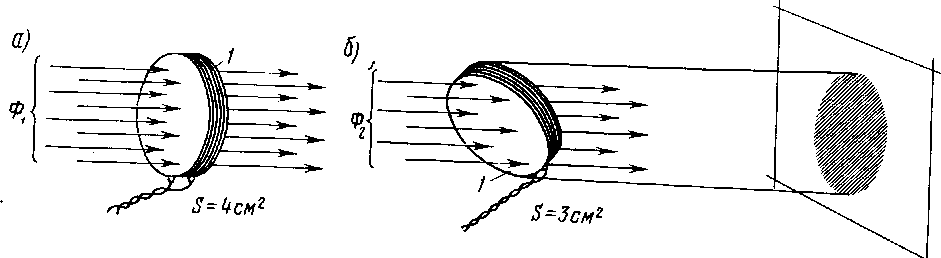
Рис. 2.4. Магнитный поток, пронизывающий катушку при перпендикулярном (а) и наклонном (б) ее положениях по отношению к направлению магнитных силовых линий
Для более наглядного изображения магнитного поля силовые линии рас-