Файл: Программа среднего профессионального образования Экономика и бухгалтерский учет (по отраслям) Дисциплина Информатика.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 27
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
АНО ПО " Открытый социально- экономический колледж"
Программа среднего профессионального образования
Экономика и бухгалтерский учет (по отраслям)
Дисциплина: Информатика
Практическое задание 4
Выполнил:
слушатель Бонатова Елена Александровна
Преподаватель:
Титов Андрей Валерьевич
г. Тула 2021
Практическое занятие 4
Вариант 1
1.Среди следующих предложений выделить высказывания, установить, истинны они или ложны:
Решение: метод решение интуитивный.
1) река Исеть впадает в Каспийское море;
Ответ: является высказыванием – истинно.
2) пейте апельсиновый сок;
Ответ: не является высказыванием.
3) все люди – братья;
Ответ: является высказыванием – ложно.
4) математическая логика – увлекательная наука;
Ответ: является высказыванием – истинно.
5) 4<5;
Ответ: является высказыванием – истинно.
6) x2-5x+9;
Ответ: не является высказыванием.
7) x2-5x+9=0
Ответ: не является высказыванием.
8) для всех натуральных чисел x и y верно равенство x+y=y+x.
Ответ: является высказыванием – истинно.
2. Составить таблицу истинности для формулы
Решение:
-
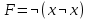
Количество строк: 2n + 1 N = 1 21 + 1 = 3 -
Количество операций: p = 3 -
Количество столбцов: n + p = 1 + 3 = 4
| х | x̅ | х˄ x̅ |  х˄ x̅ |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
3. Составить таблицы истинности для следующих формул
:
Решение:
a)
| x˄y˅z | 23 + 1= 9 |
| | 3 + 2 = 5 |
| x | y | z | x˄y | x˄y˅z |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 |
б) F = ¬ x
(
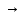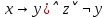
| 23 + 1 =9 | | | | | | | | |||
| 3 + 6 = 9 | | | | | | | | |||
| x | y | z | x̅ | x→y | (x→y)˄z | y̅ | (x→y)˄z˅ y̅ | F | ||
| 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | ||
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | ||
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | ||
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | ||
| 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | ||
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | ||
| 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | ||
4. Доказать равносильность следующих формул.
Доказательство:
1) x → y ≡ x ˄y̅ , так как применим закон Де Моргана для Импликации
¬ (x→y) ≡ x˄¬y
2) x ˄ y ˅ x̅ ˄ y ˅ x̅ ˄ y̅ ≡ x→y
| 22 + 1 = 5 | | | | | | | ||||
| 5 + 5 = 10 | | | | | | | ||||
| x | y | x˄y | x̅ | x̅˄y | x˄y˅x̅˄y | y̅ | x̅˄y̅ | x˄y˅x̅˄y˅x̅˄y̅ | x→y | |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | |
5. Найти СДНФ, которая определяет функцию f (x, y) по следующей таблице истинности
| x | y | z | f (x, y, z) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Решение: Найдем наборы на которые функция принимает истинное значение:
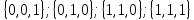
К1 :
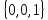- x̅ y̅zK2 :
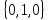- x̅y z̅К3 :
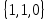- xy z̅К4 :
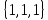– xyzОбъединим конъюнкции с помощью операции ИЛИ и получим
СДНФ = К1 ˅ K2 ˅ К3 ˅ К4 = x̅ y̅z ˅ x̅y z̅ ˅ xy z̅ ˅ xyz
Ответ: = x̅ y̅z ˅ x̅y z̅ ˅ xy z̅ ˅ xyz