Файл: Лабораторная работа 3 анализ переходных процессов в цепях первого порядка с использованием программы fastmean.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 70
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лабораторная работа № 3
АНАЛИЗ ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЦЕПЯХ ПЕРВОГО ПОРЯДКА с использованием программы FASTMEAN
1. Цель работы
Моделирование переходных процессов в цепях первого порядка с помощью программы FASTMEAN.
2. Задание на самостоятельную подготовку к работе
2.1. Изучите методы и результаты анализа переходных процессов в электрических цепях.
2.2. Рассчитайте и постройте кривые изменения напряжений ????????(????) и ????????(????) в RC-контуре (рисунок 1) для значений R1, C1, соответствующие вашему номеру варианта (таблица 1). Данные расчета занесите в таблицу 2.
Таблица 1 – Исходные данные
| Номер варианта | tи, мкс | R1, Ом | R2, Ом | С1, мкФ | С2, мкФ | С3, мкФ |
| 3 | 200 | 250 | 500 | 0,12 | 0,24 | 0,36 |
Для анализа переходного процесса при воздействии одиночного прямоугольного импульса удобно воспользоваться методом наложения, представив импульс суммой двух смещенных во времени скачков напряжения (рисунок 2), и записать искомую реакцию в следующем виде:
0≤????≤????и ????1(????)=????(????)
????≥????и ????2(????)=????(????)−????(????−????и ),
где ????(????) – реакция исследуемой цепи при воздействии постоянного напряжения. Для RC-цепи ????(????)=????????(????) или ????(????)=????????(????).
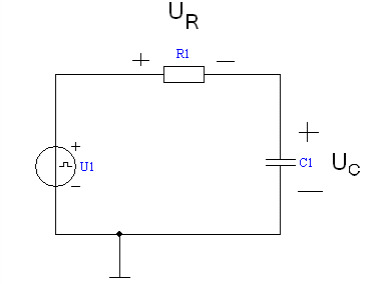
Рисунок 1
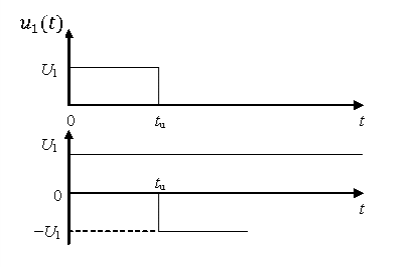
Рисунок 2
При включении RC-цепи на постоянное напряжение U1 напряжение на емкости:
????????(????)=????1(1−????− ????/???? ),
где τ = RC – постоянная времени цепи.
Следовательно, при воздействии прямоугольного импульса
????????(????)=????1(1−????− ????/???? ) при 0≤????≤????и ;
????????(????)=????1(1−????− ????и/???? )∙????− (????−????и)/???? при ????≥????и .
Выражение для тока ????(????) и напряжения на резистивном сопротивлении ????????(????) легко получить простым дифференцированием:
????(????)=????????????????(????)/????????, ????????(????)=????(????)∙????
Предварительные расчет к лабораторной работе выполним с использованием Mathcad. Ниже приведены графики, построенные с использованием Mathcad:
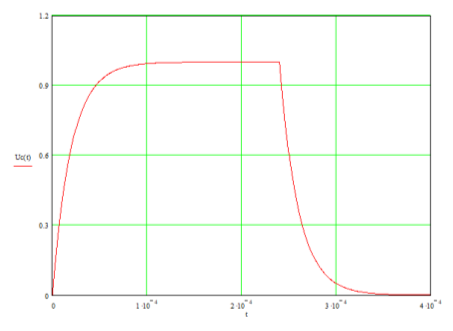
Рисунок 3 – График UC(t)
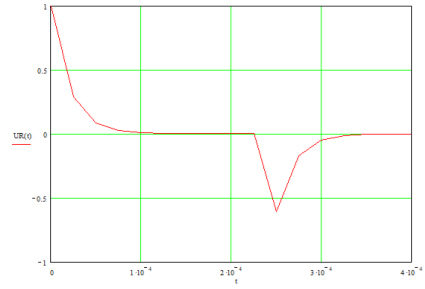
Рисунок 4 – График UR(t)
Кривые ????????(????) и ????????(????) при воздействии прямоугольного импульса напряжения на цепь приведены на рисунке 5.
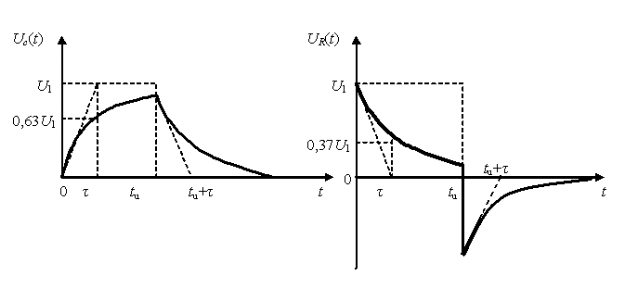
Рисунок 5
В интервале времени 0 ≤ t ≤ tи емкость заряжается и напряжение ????????(????) растет. В свободном режиме t > tи происходит разряд емкости, и напряжение ????????(????) убывает. При этом ток ????(????), а значит, и напряжение ????????(????) имеет скачки при ????=0 и ????=????и. На графиках (рисунок 5) видно, что направление тока при заряде емкости и при ее разряде – противоположны.
Длительность разряда (переходного процесса) зависит от постоянной времени и практически определяется интервалом времени (3-5) τ.
Постоянная времени легко определяется графически по любой реакции, характеризующей переходный процесс. Численно она равна длине подкасательной или определяется на уровне 0,63 U1 по кривой ????????(????) или на уровне 0,37 U1 по кривой ????????(????) (рисунок 5).
2.3. Используя приведенные соотношения и данные таблицы 1 для своего номера варианта, рассчитаем постоянную времени цепи для шести комбинаций R и С и заполним таблицу 2.
Таблица 2 – Результаты предварительного расчета для RC-контура
| 0 ≤ t ≤ tи | t ≥tи | ||||||||
| ????/???? | t, мкс | ????− ????/???? | ????????1(????), В | ????????1(????), В | (????−????и)/???? | t, мкс | ????− (????−????и)/???? | ????????1(????), В | ????????1(????), В |
| 0 | 0 | 1,000 | 0,000 | 1,000 | 0 | 240 | 1,000 | 1,000 | -1,000 |
| 0,67 | 15 | 0,513 | 0,487 | 0,513 | 0,67 | 255 | 0,513 | 0,513 | -0,513 |
| 1 | 22 | 0,369 | 0,631 | 0,369 | 1 | 262 | 0,369 | 0,369 | -0,369 |
| 1,33 | 29 | 0,266 | 0,734 | 0,266 | 1,33 | 269 | 0,266 | 0,266 | -0,266 |
| 2 | 44 | 0,136 | 0,864 | 0,136 | 2,4 | 293 | 0,091 | 0,091 | -0,091 |
| 2,4 | 53 | 0,091 | 0,909 | 0,091 | 3 | 306 | 0,050 | 0,050 | -0,050 |
| | 240 | 0,000 | 1,000 | 0,000 | 5 | 350 | 0,007 | 0,007 | -0,007 |
3. Задание по моделированию на компьютере
3.1. Загрузите программу FASTMEAN.
3.2. Построим на экране дисплея схему последовательного RC-контура, показанного на рисунке 6.
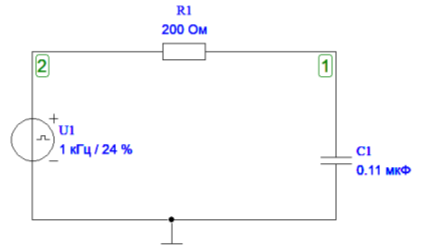
Рисунок 6
Ко входу контура подсоединим источник напряжения. Смоделируем источник прямоугольных импульсов с длительностью импульса -tи в соответствии со своим номером варианта.
Задаем следующие параметры источника напряжения:
«Тип источника» – меандр
«Частота (f)» – 1 кГц
«Коэффициент заполнения (К)» - 24 %
«Макс.напряжение (Umax)» – 1 В
«Мин.напряжение (Umin)» – 0 В
«Длительность фронта (tfr)» – 1 нс
«Задержка включение (delay)» – 0 пер
3.3. Задаем значения параметров пассивных элементов RC-контура в соответствии со своим номером варианта. В качестве начальных параметров элементов выбираем значения R=R1 и С=С1. Пронумеруем узлы, нажав кнопку в меню. Построим графики напряжений, для этого выбираем в меню «Анализ» → «Переходный процесс».
Выведем сначала на дисплей графики входного напряжения и напряжения на емкости (рисунок 7). Конечное время (tmax) в меню «Переходный процесс» возьмем равным 480 мкс, шаг расчета tmax/1000.
По графикам напряжения на емкости при помощи электронной линейки определяем значение постоянной времени цепи τ на уровне 0,63 для трех значений емкости. Измеренные значения τ запишем в таблицу 3.
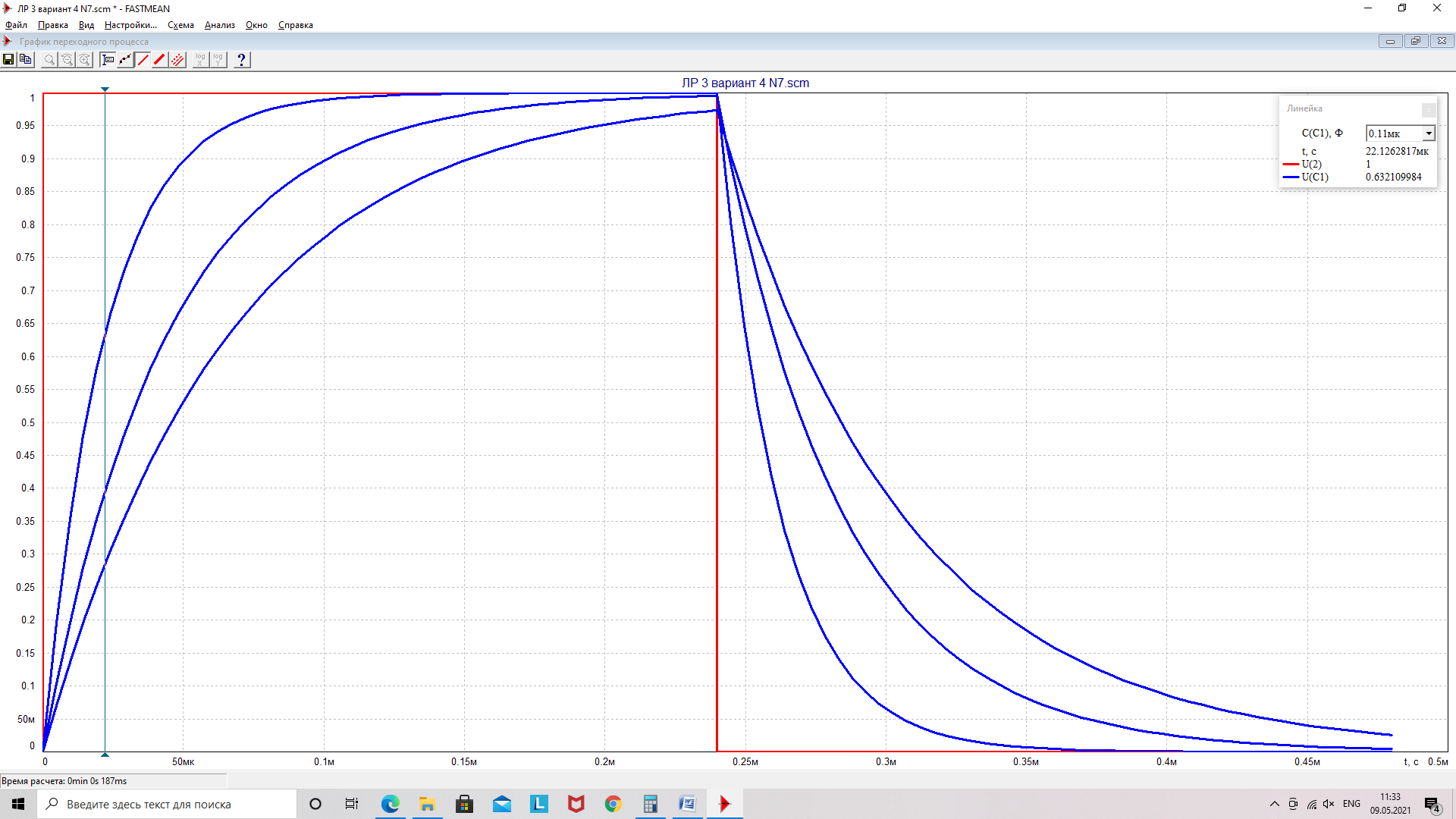
Рисунок 7 - График UC(t) при R=R1
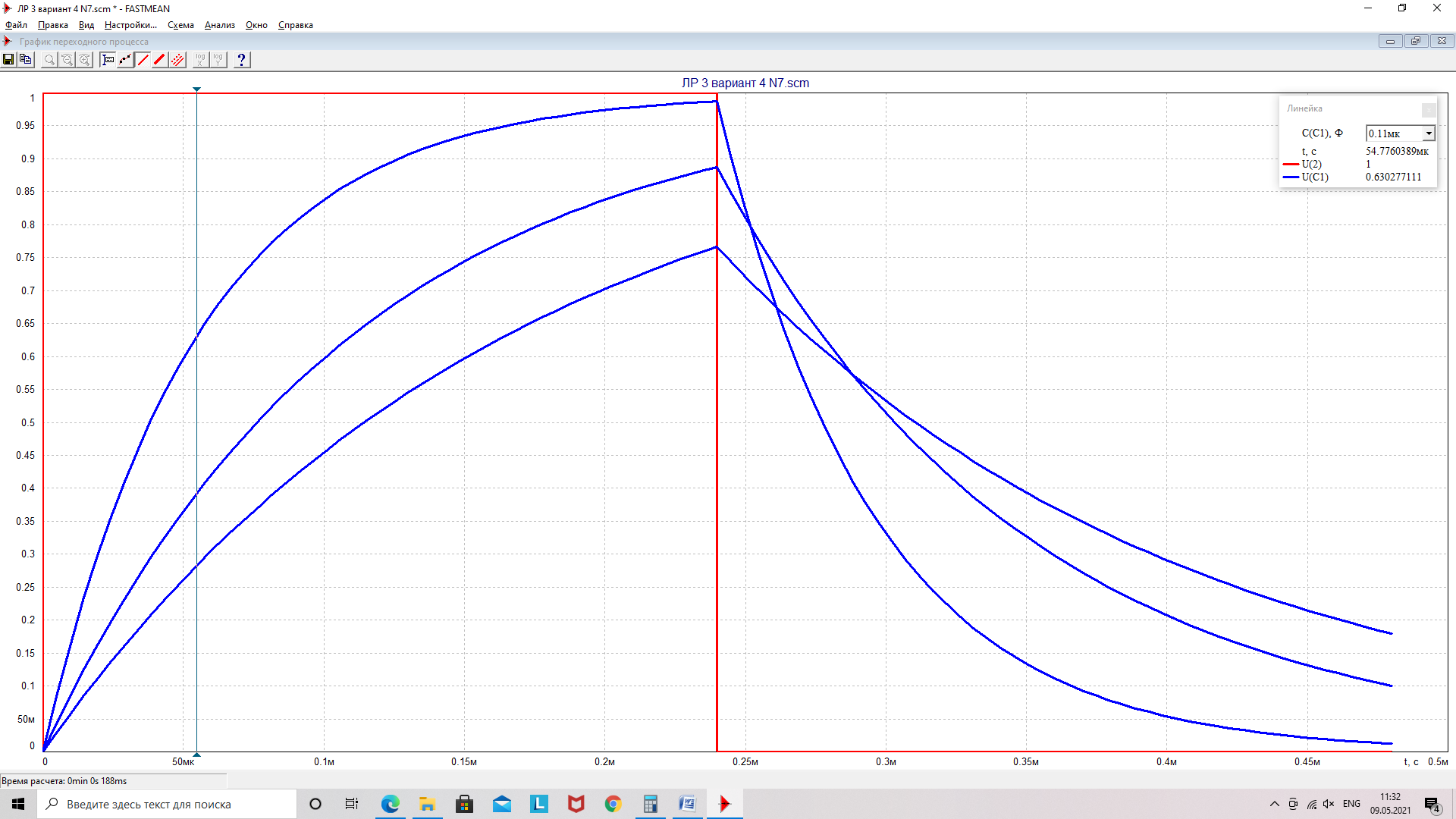
Рисунок 8 - График UC(t) при R=R2
Далее построим графики входного напряжения и напряжения на сопротивлении, заполнив таблицы анализа.
Графики напряжений будут иметь вид, как это показано на рисунке 9-10.
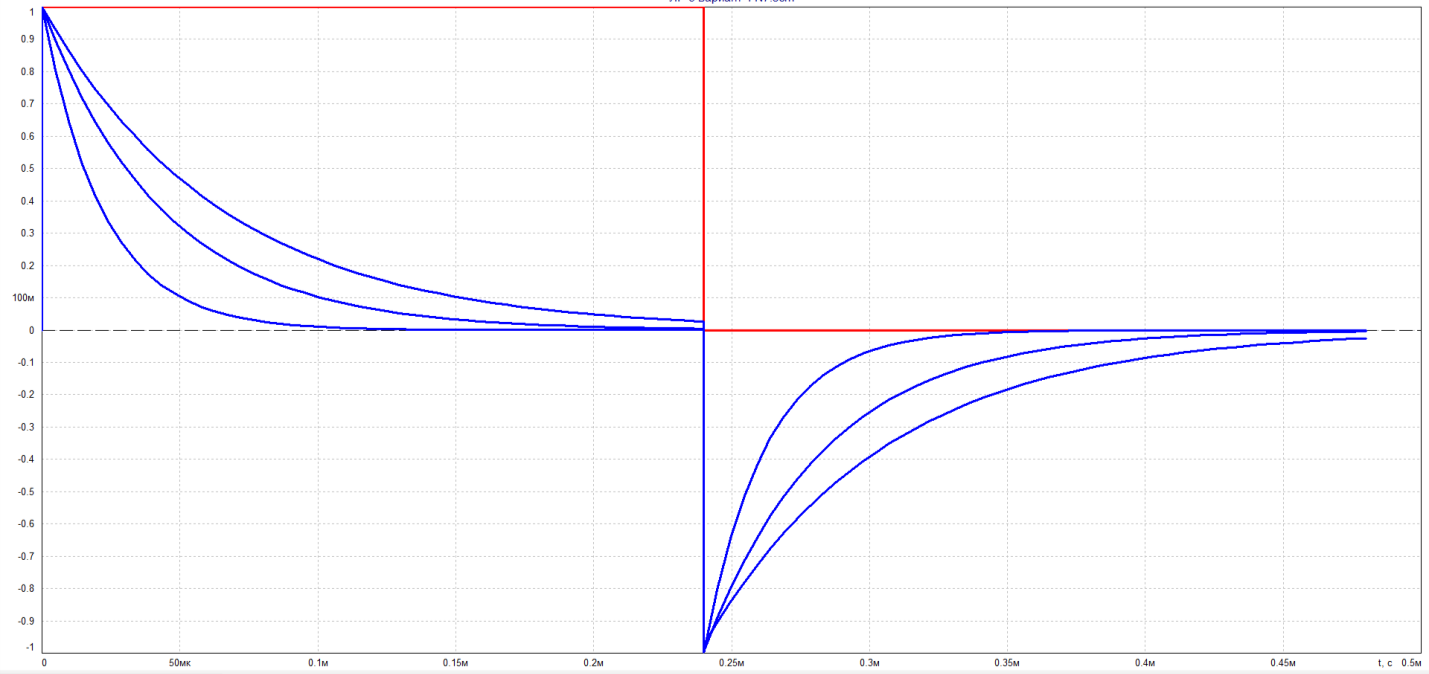
Рисунок 9 - График UR(t) при R=R1
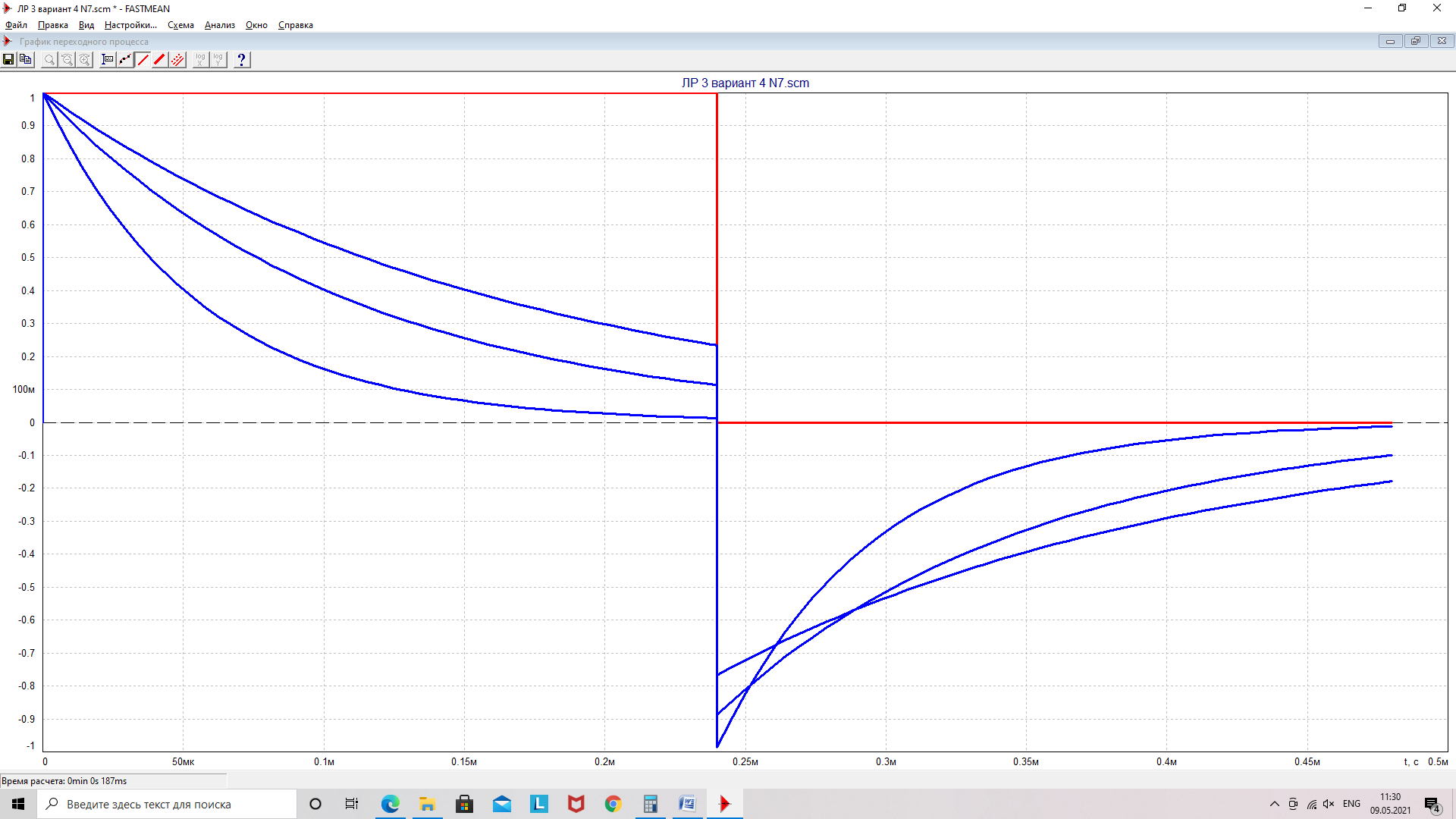
Рисунок 10 - График UR(t) при R=R2
Таблица 3 – Таблица результатов расчета и анализа на ПК для RC-контура
| | R1=200 Ом | R2=500 Ом | ||||||
| С1=0,11 | С2=0,22 | С3=0,33 | С1=0,11 | С2=0,22 | С3=0,33 | |||
| мкФ | мкФ | мкФ | мкФ | мкФ | мкФ | |||
| Результаты расчета | ????, мкс | 22 | 44 | 66 | 55 | 110 | 165 | |
| Результаты анализа на ПК | ????, мкс | 22,12 | 43,71 | 65,57 | 54,78 | 109,55 | 164,33 | |
Выводы:
Чем больше значение R, тем больше постоянная времени цепи τ. Конденсатор не успевает заряжаться, напряжение на конденсаторе меньше величины напряжения источника питания.
Чем больше значение C, тем больше постоянная времени цепи τ. Конденсатор не успевает заряжаться, напряжение на конденсаторе меньше величины напряжения источника питания.